Površina kuća je Fišerov kriterijum. Fisherova funkcija u excelu i primjeri njenog rada

Koristeći ovaj primjer, razmotrit ćemo kako se procjenjuje pouzdanost rezultirajuće regresione jednačine. Isti test se koristi za testiranje hipoteze da su koeficijenti regresije istovremeno jednaki nuli, a=0, b=0. Drugim riječima, suština proračuna je da se odgovori na pitanje: može li se koristiti za dalje analize i prognoze?

Da biste utvrdili da li su varijanse u dva uzorka slične ili različite, koristite ovaj t-test.

Dakle, svrha analize je da se dobije neka procjena pomoću koje bi se moglo reći da je na određenom nivou α rezultirajuća regresiona jednačina statistički pouzdana. Za ovo koristi se koeficijent determinacije R 2.
Testiranje značajnosti regresijskog modela provodi se korištenjem Fišerovog F testa, čija se izračunata vrijednost nalazi kao omjer varijanse originalne serije zapažanja indikatora koji se proučava i nepristrasne procjene varijanse zaostalog niza za ovaj model.
Ako je izračunata vrijednost sa k 1 =(m) i k 2 =(n-m-1) stepenima slobode veća od tabelarne vrijednosti na datom nivou značajnosti, tada se model smatra značajnim.

gdje je m broj faktora u modelu.
Ocjena statistički značaj parna soba linearna regresija izvodi se prema sljedećem algoritmu:
1. Postavlja se nulta hipoteza da je jednadžba u cjelini statistički beznačajna: H 0: R 2 =0 na nivou značajnosti α.
2. Zatim odredite stvarnu vrijednost F-kriterijuma:


gdje je m=1 za parnu regresiju.
3. Tabelarna vrijednost se određuje iz Fisherove distributivne tablice za dati nivo značajnosti, uzimajući u obzir da je broj stupnjeva slobode za ukupan zbir kvadrata (veća varijansa) 1 i broj stupnjeva slobode za ostatak zbir kvadrata (manja varijansa) u linearnoj regresiji je n-2 (ili preko Excel funkcija FDISC(vjerovatnoća,1,n-2)).
F tabela je maksimalna moguća vrednost kriterijuma pod uticajem slučajnih faktora sa datim stepenom slobode i nivoom značajnosti α. Nivo značajnosti α je vjerovatnoća odbacivanja tačne hipoteze, pod uslovom da je tačna. Obično se uzima da je α 0,05 ili 0,01.
4. Ako je stvarna vrijednost F-testa manja od vrijednosti u tabeli, onda kažu da nema razloga za odbacivanje nulte hipoteze.
U suprotnom, nulta hipoteza se odbacuje i sa vjerovatnoćom (1-α) prihvata se alternativna hipoteza o statističkom značaju jednačine u cjelini.
Tabelarna vrijednost kriterija sa stupnjevima slobode k 1 =1 i k 2 =48, F tabela = 4

Zaključci: Budući da je stvarna vrijednost F > F tabela, koeficijent determinacije je statistički značajan ( pronađena procjena jednačine regresije je statistički pouzdana) .

Analiza varijanse

.

Indikatori kvaliteta regresijske jednačine

Primjer. Na osnovu ukupno 25 trgovačkih preduzeća, proučava se odnos između sledećih karakteristika: X - cena proizvoda A, hiljada rubalja; Y - profit trgovačko preduzeće, miliona rubalja Prilikom procjene regresijskog modela dobijeni su sljedeći međurezultati: ∑(y i -y x) 2 = 46000; ∑(y i -y avg) 2 = 138000. Koji pokazatelj korelacije se može odrediti iz ovih podataka? Izračunajte vrijednost ovog indikatora na osnovu ovog rezultata i korištenja Fišerov F test izvući zaključke o kvaliteti regresijskog modela.
Rješenje. Iz ovih podataka možemo odrediti empirijski odnos korelacije: , gdje je ∑(y avg -y x) 2 = ∑(y i -y avg) 2 - ∑(y i -y x) 2 = 138000 - 46000 = 92,000.
η 2 = 92 000/138 000 = 0,67, η = 0,816 (0,7< η < 0.9 - связь между X и Y высокая).

Fišerov F test: n = 25, m = 1.
R 2 = 1 - 46000/138000 = 0,67, F = 0,67/(1-0,67)x(25 - 1 - 1) = 46. F tabela (1; 23) = 4,27
Budući da je stvarna vrijednost F > Ftable, pronađena procjena regresione jednačine je statistički pouzdana.

Pitanje: Koje statistike se koriste za testiranje značaja regresijskog modela?
Odgovor: Za značajnost cjelokupnog modela u cjelini koristi se F-statistika (Fisherov test).

Funkcija FISCHER vraća Fisherovu transformaciju argumenata u X. Ova transformacija proizvodi funkciju koja ima normalnu, a ne iskrivljenu distribuciju. FISCHER funkcija se koristi za testiranje hipoteze korištenjem koeficijenta korelacije.

Opis FISCHER funkcije u Excelu

Kada radite s ovom funkcijom, morate postaviti vrijednost varijable. Vrijedi odmah napomenuti da postoje neke situacije u kojima ova funkcija neće dati rezultate. Ovo je moguće ako je varijabla:

• nije broj. U takvoj situaciji, funkcija FISCHER će vratiti vrijednost greške #VALUE!;
• ima vrijednost manju od -1 ili veću od 1. U ovom slučaju, funkcija FISCHER će vratiti vrijednost greške #NUM!.

Jednačina koja se koristi za matematički opis funkcije FISCHER je:

Z"=1/2*ln(1+x)/(1-x)

Pogledajmo upotrebu ove funkcije koristeći 3 specifična primjera.



Procjena odnosa između dobiti i troškova korištenjem FISHER funkcije

Primer 1. Koristeći podatke o delatnosti komercijalnih organizacija, potrebno je izvršiti procenu odnosa između dobiti Y (miliona rubalja) i troškova X (miliona rubalja) koji se koriste za razvoj proizvoda (prikazano u tabeli 1).

Tabela 1 – Početni podaci:

№	X	Y
1	210.000.000,00 RUR	95.000.000,00 RUR
2	1.068.000.000,00 RUB	76.000.000,00 RUR
3	1.005.000.000,00 RUB	78.000.000,00 RUR
4	610.000.000,00 RUR	89.000.000,00 RUR
5	768.000.000,00 RUR	77.000.000,00 RUR
6	799.000.000,00 RUR	85.000.000,00 RUR

Shema za rješavanje takvih problema je sljedeća:

1. Izračunato linearni koeficijent korelacije r xy ;
2. Značajnost koeficijenta linearne korelacije provjerava se na osnovu Studentovog t-testa. U ovom slučaju postavlja se i testira hipoteza da je koeficijent korelacije jednak nuli. Za testiranje ove hipoteze koristi se t-statistika. Ako se hipoteza potvrdi, t-statistika ima Studentovu distribuciju. Ako je izračunata vrijednost t p > t cr, hipoteza se odbacuje, što ukazuje na značajnost linearnog koeficijenta korelacije, a samim tim i na statističku značajnost odnosa između X i Y;
3. Određuje se intervalna procjena za statistički značajan linearni koeficijent korelacije.
4. Intervalna procjena za koeficijent linearne korelacije određena je na osnovu inverzna z-transformacija Fisher;
5. Izračunava se standardna greška koeficijenta linearne korelacije.

Rezultati rješavanja ovog problema sa funkcijama koje se koriste u Excelu prikazani su na slici 1.

Slika 1 – Primjer proračuna.

br.	Naziv indikatora	Formula za izračun
1	Koeficijent korelacije	=CORREL(B2:B7,C2:C7)
2	Izračunata vrijednost t-testa tp	=ABS(C8)/SQRT(1-POWER(C8,2))*SQRT(6-2)
3	Vrijednost tabele t-testa trh	=STUDISCOVER(0.05,4)
4	Tabelarna vrijednost standarda normalna distribucija zy	=NORMSINV((0,95+1)/2)
5	Vrijednost Fisher z’ transformacije	=FISHER(C8)
6	Procjena lijevog intervala za z	=C12-C11*ROOT(1/(6-3))
7	Procjena desnog intervala za z	=C12+C11*KORIJEN(1/(6-3))
8	Procjena lijevog intervala za rxy	=FISHEROBR(C13)
9	Procjena desnog intervala za rxy	=FISHEROBR(C14)
10	Standardna devijacija za rxy	=ROOT((1-C8^2)/4)

Dakle, sa vjerovatnoćom od 0,95, koeficijent linearne korelacije leži u rasponu od (-0,386) do (-0,990) sa standardna greška 0,205.

Provjera statističke značajnosti regresije pomoću funkcije FASTER

Primjer 2: Testirajte statističku značajnost jednačine višestruka regresija Koristeći Fišerov F test, izvucite zaključke.

Da bismo provjerili značaj jednadžbe u cjelini, postavili smo hipotezu H 0 o statističkoj beznačajnosti koeficijenta determinacije i suprotnu hipotezu H 1 o statističkoj značajnosti koeficijenta determinacije:

H 1: R 2 ≠ 0.

Testirajmo hipoteze koristeći Fišerov F test. Indikatori su prikazani u tabeli 2.

Tabela 2 - Početni podaci

Da bismo to učinili, koristimo funkciju u Excelu:

BRŽE (α;p;n-p-1)

• α je vjerovatnoća povezana sa datom distribucijom;
• p i n su brojnik i imenilac stepena slobode, respektivno.

Znajući da je α = 0,05, p = 2 i n = 53, dobijamo sljedeću vrijednost za F crit (vidi sliku 2).

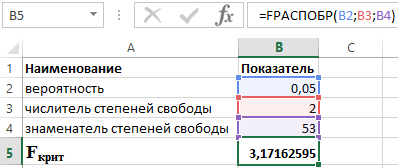
Slika 2 – Primjer proračuna.

Stoga možemo reći da je F izračunato > F kritično. Kao rezultat, prihvata se hipoteza H 1 o statističkoj značajnosti koeficijenta determinacije.

Izračunavanje vrijednosti indikatora korelacije u Excelu

Primer 3. Korišćenje podataka od 23 preduzeća o: X je cena proizvoda A, hiljada rubalja; Y je profit trgovačkog preduzeća, proučava se njihova zavisnost; Regresijski model je procijenjen na sljedeći način: ∑(yi-yx) 2 = 50000; ∑(yi-ysr) 2 = 130000. Koji pokazatelj korelacije se može odrediti iz ovih podataka? Izračunajte vrijednost indikatora korelacije i, koristeći Fisherov kriterij, izvedite zaključak o kvaliteti regresijskog modela.

Odredimo F krit iz izraza:

F izračunato = R 2 /23*(1-R 2)

gdje je R koeficijent determinacije jednak 0,67.

Dakle, izračunata vrijednost F calc = 46.

Za određivanje F krit koristimo Fisherovu distribuciju (vidi sliku 3).

Slika 3 – Primjer proračuna.

Dakle, rezultirajuća procjena regresione jednačine je pouzdana.

Fisherov kriterijum

Fisherov kriterij se koristi za testiranje hipoteze da su varijanse dvije populacije raspoređene prema normalnom zakonu jednake. To je parametarski kriterijum.

Fišerov F test naziva se omjer varijanse jer se formira kao omjer dvije nepristrasne procjene varijansi koje se upoređuju.

Neka se kao rezultat posmatranja dobiju dva uzorka. Od njih su odstupanja i vlasništvo I stepena slobode. Pretpostavićemo da je prvi uzorak uzet iz populacije sa varijansom , a drugi je iz opće populacije s varijansom . Postavlja se nulta hipoteza o jednakosti dvije varijanse, tj. H0:
ili . Da bi se ova hipoteza odbacila, potrebno je dokazati značaj razlike na datom nivou značajnosti
.

Vrijednost kriterija se izračunava pomoću formule:

Očigledno, ako su varijanse jednake, vrijednost kriterija će biti jednaka jedinici. U drugim slučajevima bit će veći (manji) od jedan.

Test ima Fisherovu distribuciju
. Fisherov test - dvostrani test i nulta hipoteza
odbijen u korist alternative
Ako . Evo gde
– volumen prvog i drugog uzorka, respektivno.

Sistem STATISTICA implementira jednostrani Fisher test, tj. maksimalna varijansa se uvijek uzima kao kvalitet. U ovom slučaju, nulta hipoteza se odbacuje u korist alternative if.

Primjer

Neka se postavi zadatak da se uporedi efikasnost podučavanja dve grupe učenika. Nivo postignuća karakteriše nivo upravljanja procesom učenja, a disperzija je kvalitet upravljanja učenjem, stepen organizacije procesa učenja. Oba indikatora su nezavisna i opšti slučaj moraju se razmatrati zajedno. Nivo akademskog uspjeha (matematičko očekivanje) svake grupe studenata karakteriziraju aritmetički prosjek i , a kvalitet karakteriziraju odgovarajuće uzorne varijanse procjena: i . Prilikom procjene nivoa trenutnog učinka, pokazalo se da je isti kod oba učenika: = = 4,0. Primjeri varijacija:
I
. Brojevi stepeni slobode koji odgovaraju ovim procjenama:
I
. Odavde, za utvrđivanje razlika u efektivnosti učenja, možemo koristiti stabilnost akademskog učinka, tj. Hajde da testiramo hipotezu.

Hajde da izračunamo
(trebalo bi da postoji velika varijansa u brojiocu), . Prema tabelama ( STATISTICA – VjerovatnoćaDistribucijaKalkulator) nalazimo , što je manje od izračunatog, stoga nultu hipotezu treba odbaciti u korist alternative. Ovaj zaključak možda neće zadovoljiti istraživača, jer ga zanima prava vrijednost omjera
(u brojniku uvijek imamo veliku varijansu). Prilikom provjere jednostranog kriterija, nalazimo da je manji od gore izračunate vrijednosti. Dakle, nulta hipoteza se mora odbaciti u korist alternative.

Fisher test u programu STATISTICA u Windows okruženju

Za primjer testiranja hipoteze (Fisherov kriterij), koristimo (kreiramo) datoteku s dvije varijable (fisher.sta):

Rice. 1. Tabela sa dvije nezavisne varijable

Za testiranje hipoteze potrebno je u osnovnoj statistici ( BasicStatistikaiStolovi) odaberite t-test za nezavisne varijable. ( t-test, nezavisan, po varijablama).

Rice. 2. Testiranje parametarskih hipoteza

Nakon odabira varijabli i pritiska na tipku Rezime Izračunavaju se vrijednosti standardnih devijacija i Fisherov kriterij. Pored toga, utvrđuje se i nivo značajnosti str, u kojem je razlika neznatna.

Rice. 3. Rezultati testiranja hipoteza (F-test)

Koristeći VjerovatnoćaKalkulator i postavljanjem vrijednosti parametara, možete izgraditi graf Fisherove distribucije sa označenom izračunatom vrijednošću.

Rice. 4. Područje prihvatanja (odbacivanja) hipoteze (F-kriterijum)

Izvori.

Testiranje hipoteza o odnosu između dvije varijanse

URL: /tryfonov3/terms3/testdi.htm

Predavanje 6. :8080/resources/math/mop/lections/lection_6.htm

F – Fišerov kriterijum

URL: /home/portal/applications/Multivariatadvisor/F-Fisher/F-Fisheer.htm

Teorija i praksa probabilističkih statističkih istraživanja.

URL: /active/referats/read/doc-3663-1.html

F – Fišerov kriterijum

Fisherov kriterijum omogućava vam da uporedite varijanse uzorka dva nezavisna uzorka. Da biste izračunali F emp, potrebno je pronaći omjer varijansi dva uzorka, tako da je veća varijansa u brojiocu, a manja u nazivniku. Formula za izračunavanje Fisherovog kriterija je:

gdje su varijanse prvog i drugog uzorka, respektivno.

Pošto, prema uslovima kriterijuma, vrednost brojila mora biti veća ili jednaka vrednosti nazivnika, vrednost F emp će uvek biti veća ili jednaka jedinici.

Broj stepeni slobode se takođe jednostavno određuje:

k 1 =n l - 1 za prvi uzorak (tj. za uzorak čija je varijansa veća) i k 2 = n 2 - 1 za drugi uzorak.

U Dodatku 1, kritične vrijednosti Fisherovog kriterija nalaze se vrijednostima k 1 (gornji red tabele) i k 2 (lijeva kolona tabele).

Ako je t em >t crit, tada se prihvata nulta hipoteza, u suprotnom se prihvata alternativa.

Primjer 3. Testiranje je obavljeno u dva treća razreda mentalni razvoj deset učenika na TURMSH testu. Dobijene prosječne vrijednosti nisu se značajno razlikovale, ali psihologa zanima pitanje da li postoje razlike u stepenu homogenosti pokazatelja mentalnog razvoja između razreda.

Rješenje. Za Fisherov test potrebno je uporediti varijanse rezultata testa u oba razreda. Rezultati ispitivanja su predstavljeni u tabeli:

Tabela 3.

Student br.	Prva klasa	Druga klasa

Nakon što smo izračunali varijanse za varijable X i Y, dobijamo:

s x 2 =572,83; s y 2 =174,04

Zatim, koristeći formulu (8) za izračunavanje po Fisherovom F kriteriju, nalazimo:

Prema tabeli iz Dodatka 1 za F kriterijum sa stepenom slobode u oba slučaja jednakim k = 10 - 1 = 9, nalazimo F crit = 3,18 (<3.29), следовательно, в терминах статистических гипотез можно утвер­ждать, что Н 0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н 1 . Иcследователь может утверждать, что по степени однородности такого показа­теля, как умственное развитие, имеется различие между выбор­ками из двух классов.

6.2 Neparametarski testovi

Uspoređujući na oko (procentualno) rezultate prije i nakon bilo kakvog udara, istraživač dolazi do zaključka da ako se uoče razlike, onda postoji razlika u uzorcima koji se porede. Ovaj pristup je kategorički neprihvatljiv, jer je za procente nemoguće odrediti nivo pouzdanosti razlika. Procenti uzeti sami po sebi ne omogućavaju izvođenje statistički pouzdanih zaključaka. Da bi se dokazala efikasnost bilo koje intervencije, neophodno je identifikovati statistički značajan trend u pristrasnosti (pomeranju) indikatora. Da bi riješio takve probleme, istraživač može koristiti niz kriterija diskriminacije. U nastavku ćemo razmotriti neparametarske testove: test znakova i hi-kvadrat test.

)

Izračun kriterija φ*

1. Odredite one vrijednosti atributa koje će biti kriterij za podjelu subjekata na one koji „imaju učinak“ i one koji „nemaju učinak“. Ako se karakteristika mjeri kvantitativno, upotrijebite λ kriterij za pronalaženje optimalne točke razdvajanja.

2. Nacrtajte tabelu sa četiri ćelije (sinonim: četiri polja) sa dve kolone i dva reda. Prva kolona je “postoji efekat”; druga kolona - “bez efekta”; prvi red odozgo - 1 grupa (uzorak); drugi red - grupa 2 (uzorak).

4. Prebrojite broj ispitanika u prvom uzorku koji nemaju efekta i unesite ovaj broj u gornju desnu ćeliju tabele. Izračunajte zbir gornje dvije ćelije. Trebalo bi da se podudara sa brojem subjekata u prvoj grupi.

6. Izbrojite broj ispitanika u drugom uzorku koji nemaju efekta i unesite ovaj broj u donju desnu ćeliju tabele. Izračunajte zbir dvije donje ćelije. Trebalo bi da se podudara sa brojem ispitanika u drugoj grupi (uzorak).

7. Odrediti postotak ispitanika koji „imaju efekta“ povezujući njihov broj sa ukupnim brojem ispitanika u datoj grupi (uzorku). Rezultirajuće procente upišite u gornju lijevu i donju lijevu ćeliju tabele u zagradama, kako ih ne biste brkali s apsolutnim vrijednostima.

8. Provjerite da li je jedan od postotaka koji se porede jednak nuli. Ako je to slučaj, pokušajte to promijeniti pomicanjem točke razdvajanja grupe u jednom ili drugom smjeru. Ako je to nemoguće ili nepoželjno, napustite φ* kriterij i koristite kriterij χ2.

9. Odredite prema tabeli. XII Dodatak 1 uglovi φ za svaki od upoređenih postotaka.

gdje je: φ1 - ugao koji odgovara većem procentu;

φ2 - ugao koji odgovara manjem procentu;

N1 - broj opservacija u uzorku 1;

N2 - broj zapažanja u uzorku 2.

11. Uporedi dobijenu vrijednost φ* sa kritičnim vrijednostima: φ* ≤1,64 (p<0,05) и φ* ≤2,31 (р<0,01).

Ako je φ*emp ≤φ*cr. H0 je odbijen.

Ako je potrebno, odredite tačan nivo značajnosti rezultujućeg φ*emp prema tabeli. XIII Dodatak 1.

Ova metoda je opisana u mnogim priručnicima (Plokhinsky N.A., 1970; Gubler E.V., 1978; Ivanter E.V., Korosov A.V., 1992, itd.) Ovaj opis se zasniva na verziji metode koju je razvio i predstavio E.V. Gubler.

Svrha kriterija φ*

Fišerov kriterijum je dizajniran da uporedi dva uzorka prema učestalosti pojavljivanja efekta (indikatora) od interesa za istraživača. Što je veći, to su razlike pouzdanije.

Opis kriterijuma

Kriterijumom se vrednuje pouzdanost razlika između onih procenata dva uzorka u kojima je zabeležen efekat (indikator) koji nas zanima. Slikovito rečeno, upoređujemo 2 najbolja komada izrezana od 2 pite i odlučujemo koji je istinski veći.

Suština Fisherove kutne transformacije je pretvaranje postotaka u vrijednosti centralnog ugla, koji se mjere u radijanima. Veći procenat će odgovarati većem uglu φ, a manji procenat će odgovarati manjem uglu, ali odnosi ovde nisu linearni:

gdje je P postotak izražen u dijelovima jedinice (vidi sliku 5.1).

Sa povećanjem neslaganja između uglova φ 1 i φ 2 a povećanjem broja uzoraka vrijednost kriterija raste. Što je veća vrijednost φ*, vjerovatnije je da su razlike značajne.

Hipoteze

H 0 : Proporcija osoba, u kojima se manifestuje proučavani efekat, u uzorku 1 nema više nego u uzorku 2.

H 1 : Udio pojedinaca koji pokazuju proučavani učinak veći je u uzorku 1 nego u uzorku 2.

Grafički prikaz kriterija φ*

Metoda kutne transformacije je nešto apstraktnija od ostalih kriterija.

Formula koju slijedi E.V.Gubler pri izračunavanju vrijednosti φ pretpostavlja da 100% čini ugao φ=3,142, odnosno zaokruženu vrijednost π=3,14159... To nam omogućava da uporedne uzorke predstavimo u obliku. dva polukruga, od kojih svaki simbolizira 100% populacije svog uzorka. Procenti subjekata sa “efektom” biće predstavljeni kao sektori formirani od centralnih uglova φ. Na sl. Na slici 5.2 prikazana su dva polukruga koja ilustruju primer 1. U prvom uzorku, 60% ispitanika je rešilo problem. Ovaj procenat odgovara uglu φ=1,772. U drugom uzorku, 40% ispitanika je riješilo problem. Ovaj procenat odgovara uglu φ =1,369.

Kriterijum φ* vam omogućava da odredite da li je jedan od uglova zaista statistički značajno superiorniji od drugog za date veličine uzorka.

Ograničenja kriterija φ*

1. Nijedna od proporcija koje se porede ne bi trebalo da bude nula. Formalno, ne postoje prepreke za korištenje φ metode u slučajevima kada je udio zapažanja u jednom od uzoraka jednak 0. Međutim, u tim slučajevima može se pokazati da je rezultat neopravdano naduvan (Gubler E.V., 1978, str. 86).

2. Gornji nema ograničenja u φ kriteriju - uzorci mogu biti veliki koliko želite.

Niže granica - 2 zapažanja u jednom od uzoraka. Međutim, moraju se poštovati sljedeći omjeri u broju dva uzorka:

a) ako jedan uzorak ima samo 2 opažanja, onda drugi mora imati najmanje 30:

b) ako jedan od uzoraka ima samo 3 zapažanja, onda drugi mora imati najmanje 7:

c) ako jedan od uzoraka ima samo 4 opažanja, onda drugi mora imati najmanje 5:

d) kodn 1 , n 2 ≥ 5 Moguća su bilo kakva poređenja.

U principu, takođe je moguće porediti uzorke koji ne ispunjavaju ovaj uslov, na primer, sa relacijomn 1 =2, n 2 = 15, ali u tim slučajevima neće biti moguće uočiti značajne razlike.

Kriterijum φ* nema drugih ograničenja.

Pogledajmo nekoliko primjera kako bismo ilustrirali mogućnostikriterijum φ*.

Primjer 1: poređenje uzoraka prema kvalitativno definisanoj karakteristici.

Primjer 2: poređenje uzoraka prema kvantitativno izmjerenoj karakteristici.

Primjer 3: poređenje uzoraka prema nivou i distribuciji karakteristike.

Primjer 4: Korištenje kriterija φ* u kombinaciji s kriterijemX Kolmogorov-Smirnov kako bi se postigao što precizniji rezultat.

Primjer 1 - poređenje uzoraka prema kvalitativno definisanoj karakteristici

U ovoj upotrebi kriterijuma poredimo procenat ispitanika u jednom uzorku koji karakteriše neki kvalitet sa procentom ispitanika u drugom uzorku koji karakteriše isti kvalitet.

Recimo da nas zanima da li se dvije grupe učenika razlikuju po uspješnosti u rješavanju novog eksperimentalnog problema. U prvoj grupi od 20 ljudi, 12 ljudi je izašlo na kraj, au drugom uzorku od 25 ljudi - 10. U prvom slučaju procenat onih koji su rešili problem biće 12/20·100%=60%, a u drugom 10/25·100%= 40%. Da li se ovi procenti značajno razlikuju s obzirom na podatke?n 1 In 2 ?

Čini se da se čak i „na oko“ može utvrditi da je 60% znatno više od 40%. Međutim, u stvari, ove razlike, s obzirom na podatken 1 , n 2 nepouzdan.

Hajde da to proverimo. Pošto nas zanima činjenica rješavanja problema, uspjeh u rješavanju eksperimentalnog problema smatrat ćemo „efektom“, a neuspjeh u njegovom rješavanju kao odsustvo efekta.

Hajde da formulišemo hipoteze.

H 0 : Proporcija osobaU prvoj grupi nije bilo više ljudi koji su završili zadatak nego u drugoj grupi.

H 1 : Udio ljudi koji su završili zadatak u prvoj grupi je veći nego u drugoj grupi.

Sada napravimo takozvanu tabelu sa četiri ćelije, ili tabelu sa četiri polja, koja je zapravo tabela empirijskih frekvencija za dve vrednosti atributa: "postoji efekat" - "nema efekta".

Tabela 5.1

Četvoroćelijska tabela za izračunavanje kriterijuma pri poređenju dve grupe ispitanika prema procentu onih koji su rešili zadatak.

Grupe	„Postoji efekat“: problem rešen			"Nema efekta": problem nije riješen			Iznosi
	Količina subjekti	% dijeliti		Količina subjekti	% udjela
1 grupa		(60%)			(40%)
2. grupa		(40%)			(60%)
Iznosi

U tabeli sa četiri ćelije, po pravilu, kolone „Postoji efekat” i „Nema efekta” su označene na vrhu, a redovi „Grupa 1” i „Grupa 2” su na levoj strani. U stvari, samo polja (ćelije) A i B su uključena u poređenje, odnosno procentualni udjeli u koloni „Postoji efekat“.

Prema tabeli.XIIU Dodatku 1 određuju se vrijednosti φ koje odgovaraju procentualnim udjelima u svakoj od grupa.

Sada izračunajmo empirijsku vrijednost φ* koristeći formulu:

gdje je φ 1 - ugao koji odgovara većem % udjela;

φ 2 - ugao koji odgovara manjem % udjela;

n 1 - broj zapažanja u uzorku 1;

n 2 - broj zapažanja u uzorku 2.

u ovom slučaju:

Prema tabeli.XIIIU Dodatku 1 utvrđujemo koji nivo značajnosti odgovara φ* em=1,34:

p=0,09

Također je moguće ustanoviti kritične vrijednosti φ* koje odgovaraju nivoima statističke značajnosti prihvaćenim u psihologiji:

Hajde da napravimo "os značaja".

Dobijena empirijska vrijednost φ* je u zoni beznačajnosti.

odgovor: H 0 prihvaćeno. Procenat ljudi koji su završili zadatakVu prvoj grupi ne više nego u drugoj grupi.

Može se samo suosjećati s istraživačem koji smatra da su razlike od 20% pa čak i 10% značajne bez provjere njihove pouzdanosti pomoću φ* kriterija. U ovom slučaju, na primjer, samo bi razlike od najmanje 24,3% bile značajne.

Čini se da kada uporedimo dva uzorka na bilo kojoj kvalitativnoj osnovi, kriterijum φ može nas učiniti tužnim, a ne srećnim. Ono što se činilo značajnim možda i nije tako sa statističke tačke gledišta.

Fisherov kriterij ima mnogo više mogućnosti da zadovolji istraživača kada uporedimo dva uzorka prema kvantitativno izmjerenim karakteristikama i može varirati “efekat”.

Primjer 2 - poređenje dva uzorka prema kvantitativno izmjerenoj karakteristici

U ovoj upotrebi kriterijuma, poredimo procenat ispitanika u jednom uzorku koji postižu određeni nivo vrednosti atributa sa procentom ispitanika koji postižu ovaj nivo u drugom uzorku.

U studiji G. A. Tlegenove (1990), od 70 mladih učenika stručnih škola uzrasta od 14 do 16 godina, na osnovu rezultata odabrano je 10 ispitanika sa visokim rezultatom na skali agresivnosti i 11 ispitanika sa niskim rezultatom na skali agresivnosti. ankete koristeći Freiburški upitnik ličnosti. Potrebno je utvrditi da li se grupe agresivnih i neagresivnih mladića razlikuju po distanci koju spontano biraju u razgovoru sa kolegom. Podaci G. A. Tlegenove prikazani su u tabeli. 5.2. Možete primijetiti da agresivni mladići češće biraju distancu od 50cm ili čak i manje, dok neagresivni dječaci češće biraju udaljenost veću od 50 cm.

Sada možemo smatrati razdaljinu od 50 cm kritičnom i pretpostaviti da ako je udaljenost koju je subjekt izabrao manja ili jednaka 50 cm, tada „postoji efekat“, a ako je odabrana udaljenost veća od 50 cm, tada "nema efekta." Vidimo da se u grupi agresivnih mladića efekat primećuje u 7 od 10, odnosno u 70% slučajeva, a u grupi neagresivnih mladića - u 2 od 11, odnosno u 18,2% slučajeva. . Ovi procenti se mogu porediti korišćenjem φ* metode da bi se utvrdila značajnost razlika između njih.

Tabela 5.2

Indikatori udaljenosti (u cm) koje biraju agresivni i neagresivni mladići u razgovoru sa kolegom (prema G.A. Tlegenova, 1990.)

	Grupa 1: dječaci sa visokim ocjenama na skali agresivnostiFPI- R (n 1 =10)		Grupa 2: dječaci sa niskim vrijednostima na skali agresivnostiFPI- R (n 2 =11)
	d(c m )	% udjela	d(c M )	% udjela
„Jedi efekat" d≤50cm
				18,2%
„Ne efekat" d>50 cm
	80 QO			81,8%
Iznosi		100%		100%
Prosjek	5b:o		77.3

Hajde da formulišemo hipoteze.

H 0 d ≤ 50 cm, u grupi agresivnih dječaka nema više nego u grupi neagresivnih dječaka.

H 1 : Udio ljudi koji biraju udaljenostd≤ 50 cm, više u grupi agresivnih mladića nego u grupi neagresivnih mladića. Sada napravimo takozvanu tabelu sa četiri ćelije.

Tabela 53

Četvoroćelijska tablica za izračunavanje φ* kriterija prilikom poređenja grupa agresivnih (nf=10) i neagresivni mladići (n2=11)

Grupe	"Postoji efekat": d≤50			"Nema efekta." d>50			Iznosi
	Broj predmeta	(% udjela)		Broj predmeta	(% udjela)
Grupa 1 - agresivni mladići		(70%)			(30%)
Grupa 2 - neagresivni mladići		(180%)			(81,8%)
Sum

Prema tabeli.XIIDodatak 1 određuje vrijednosti φ koje odgovaraju procentualnim udjelima “efekta” u svakoj od grupa.

Dobijena empirijska vrijednost φ* je u zoni značajnosti.

odgovor: H 0 odbijeno. PrihvaćenoH 1 . Udio ljudi koji biraju udaljenost u razgovoru manju ili jednaku 50 cm veći je u grupi agresivnih mladića nego u grupi neagresivnih mladića

Na osnovu dobijenih rezultata možemo zaključiti da agresivniji mladići češće biraju distancu manju od pola metra, dok neagresivni mladići češće biraju udaljenost veću od pola metra. Vidimo da agresivni mladići zapravo komuniciraju na granici između intimne (0-46 cm) i lične zone (od 46 cm). Sjećamo se, međutim, da je intimna udaljenost između partnera prerogativ ne samo bliskih, dobrih odnosa, već iIborba prsa u prsa (HallE. T., 1959).

Primjer 3 - poređenje uzoraka prema nivou i distribuciji karakteristike.

U ovom slučaju upotrebe, prvo možemo testirati da li se grupe razlikuju po nivoima neke osobine, a zatim uporediti distribuciju osobine u dva uzorka. Takav zadatak može biti relevantan kada se analiziraju razlike u rasponima ili obliku distribucije ocjena koje su subjekti dobili koristeći bilo koju novu tehniku.

U studiji R. T. Chirkina (1995) po prvi put je korišten upitnik koji je imao za cilj identificirati sklonost potiskivanju činjenica, imena, namjera i metoda djelovanja iz sjećanja zbog ličnih, porodičnih i profesionalnih kompleksa. Upitnik je kreiran uz učešće E.V. Sidorenka na osnovu materijala iz knjige 3. Freud “Psihopatologija svakodnevnog života”. Uzorak od 50 studenata Pedagoškog zavoda, neoženjenih, bez djece, starosti od 17 do 20 godina, ispitan je ovim upitnikom, kao i tehnikom Menester-Corzini za utvrđivanje intenziteta osjećaja lične insuficijencije,ili"kompleks inferiornosti" (ManasterG. J., CorsiniR. J., 1982).

Rezultati istraživanja prikazani su u tabeli. 5.4.

Može li se reći da postoje značajne veze između indikatora energije potiskivanja, dijagnosticirane upitnikom, i pokazatelja intenziteta osjećaja vlastite nedovoljnosti?

Tabela 5.4

Pokazatelji intenziteta osjećaja lične insuficijencije u grupama učenika sa visokim (nj=18) i niska (n2=24) energija pomaka

Grupa 1: energija pomaka od 19 do 31 poen (n 1 =181		Grupa 2: energija pomaka od 7 do 13 bodova (n 2 =24)
0; 0; 0; 0; 0 20; 20 30; 30; 30; 30; 30; 30; 30 50; 50 60; 60		0; 0 5; 5; 5; 5 10; 10; 10; 10; 10; 10 15; 15 20; 20; 20; 20 30; 30; 30; 30; 30; 30
Iznosi Prosjek	26,11	15,42

Unatoč činjenici da je prosječna vrijednost u grupi sa snažnijom represijom viša, u njoj se također uočava 5 nultih vrijednosti. Ako uporedimo histograme distribucije ocjena u dva uzorka, između njih se otkriva upečatljiv kontrast (slika 5.3).

Za poređenje dvije distribucije mogli bismo primijeniti testχ 2 ili kriterijumλ , ali za to bismo morali povećati redove, i pored toga, u oba uzorkan <30.

Kriterijum φ* će nam omogućiti da provjerimo učinak neslaganja između dvije distribucije uočene na grafu ako se složimo da pretpostavimo da “postoji efekat” ako indikator osjećaja nedovoljnosti uzme ili vrlo nizak (0) ili, obrnuto , vrlo visoke vrijednosti (S30), te da „nema efekta“ ako indikator osjećaja nedovoljnosti uzme prosječne vrijednosti, od 5 do 25.

Hajde da formulišemo hipoteze.

H 0 : Ekstremne vrijednosti indeksa deficijencije (0 ili 30 ili više) u grupi sa snažnijom represijom nisu češće nego u grupi sa manje energičnom potiskom.

H 1 : Ekstremne vrijednosti indeksa deficita (0 ili 30 ili više) u grupi sa snažnijom represijom češće su nego u grupi sa manje energičnom represijom.

Kreirajmo tabelu sa četiri ćelije pogodnu za dalje izračunavanje φ* kriterijuma.

Tabela 5.5

Četvoroćelijska tablica za izračunavanje kriterija φ* prilikom poređenja grupa sa višom i nižom energijom potiskivanja na osnovu omjera indikatora insuficijencije

Grupe	„Postoji efekat“: indikator nedostatka je 0 ili >30		“Nema efekta”: indeks neuspjeha od 5 do 25		Iznosi
		(88,9%)		(11,1%)
		(33,3%)		(66,7%)
Iznosi

Prema tabeli.XIIU Dodatku 1 određujemo vrijednosti φ koje odgovaraju upoređenim procentima:

Izračunajmo empirijsku vrijednost φ*:

Kritične vrijednosti φ* za bilo kojen 1 , n 2 , kao što se sjećamo iz prethodnog primjera, su:

TableXIIIDodatak 1 nam omogućava da preciznije odredimo nivo značajnosti dobijenog rezultata: str<0,001.

odgovor: H 0 odbijeno. PrihvaćenoH 1 . Ekstremne vrijednosti indeksa deficita (0 ili 30 ili više) u grupi sa većom energijom potiskivanja javljaju se češće nego u grupi sa manjom energijom represije.

Dakle, subjekti sa većom energijom potiskivanja mogu imati i vrlo visoke (30 ili više) i vrlo niske (nula) pokazatelje osjećaja vlastite insuficijencije. Može se pretpostaviti da potiskuju i svoje nezadovoljstvo i potrebu za uspjehom u životu. Ove pretpostavke trebaju dalje testiranje.

Dobijeni rezultat, bez obzira na njegovu interpretaciju, potvrđuje mogućnosti φ* kriterijuma u proceni razlika u obliku distribucije osobine u dva uzorka.

U originalnom uzorku bilo je 50 ljudi, ali njih 8 je isključeno iz razmatranja jer imaju prosječan rezultat na indeksu represivne anergije (14-15). Njihovi pokazatelji intenziteta osjećaja insuficijencije su također prosječni: 6 vrijednosti od po 20 bodova i 2 vrijednosti od po 25 bodova.

Snažne mogućnosti φ* kriterija mogu se provjeriti potvrđivanjem potpuno drugačije hipoteze prilikom analize materijala ovog primjera. Možemo dokazati, na primjer, da je u grupi sa većom energijom potiskivanja stopa insuficijencije i dalje veća, uprkos paradoksalnoj prirodi njene distribucije u ovoj grupi.

Hajde da formulišemo nove hipoteze.

H 0 Najveće vrijednosti indeksa deficita (30 ili više) u grupi sa većom energijom potiskivanja nisu češće nego u grupi sa manjom energijom represije.

H 1 : Najveće vrijednosti indeksa deficita (30 ili više) u grupi sa većom energijom potiskivanja javljaju se češće nego u grupi sa manjom energijom represije. Napravimo tabelu sa četiri polja koristeći podatke u tabeli. 5.4.

Tabela 5.6

Četvoroćelijska tablica za izračunavanje kriterija φ* prilikom poređenja grupa sa većom i manjom energijom potiskivanja prema nivou indikatora insuficijencije

Grupe	Indikator kvara „Postoji efekat“* je veći ili jednak 30		“Nema efekta”: stopa kvarova je manja 30		Iznosi
Grupa 1 - sa većom energijom pomaka		(61,1%)		(38.9%)
Grupa 2 - sa manjom energijom pomaka		(25.0%)		(75.0%)
Iznosi

Prema tabeli.XIIIU Dodatku 1 utvrđujemo da ovaj rezultat odgovara nivou značajnosti p = 0,008.

odgovor: Ali to je odbijeno. PrihvaćenoHj: Najveći pokazatelji nedostatka (30 ili više bodova) u grupiWithsa većom energijom pomaka javljaju se češće nego u grupi sa manjom energijom pomaka (p = 0,008).

Dakle, uspjeli smo to dokazatiVgrupaWithuz energičniju represiju prevladavaju ekstremne vrijednosti indikatora insuficijencije i činjenica da ovaj indikator prelazi njegove vrijednostidosegaupravo u ovoj grupi.

Sada bismo mogli pokušati dokazati da su u grupi sa višom energijom potiskivanja češće niže vrijednosti indeksa insuficijencije, uprkos činjenici da je prosječna vrijednostV ova grupa ima više (26,11 prema 15,42 u grupiWith manje pomaka).

Hajde da formulišemo hipoteze.

H 0 : Najniže stope nedostatka (nula) u grupiWith represije sa većom energijom nisu ništa češće nego u grupiWith manje energije pomaka.

H 1 : Najniže stope nedostatka (nula).V grupa sa većom energijom potiskivanja češće nego u grupiWith manje energične represije. Grupirajmo podatke u novu tabelu sa četiri ćelije.

Tabela 5.7

Tabela sa četiri ćelije za poređenje grupa sa različitim energijama potiskivanja na osnovu učestalosti nulte vrednosti indikatora nedostatka

Grupe	"Postoji efekat": indikator kvara je 0		"Nema efekta" insuficijencije	indikator nije jednak 0	Iznosi
Grupa 1 - sa većom energijom pomaka		(27,8%)		(72,2%)
1 grupa - sa manjom energijom pomaka		(8,3%)		(91,7%)
Iznosi

Određujemo vrijednosti φ i izračunavamo vrijednost φ*:

odgovor: H 0 odbijeno. Najniži indeksi insuficijencije (nula) u grupi sa većom energijom potiskivanja češći su nego u grupi sa manjom energijom represije (p<0,05).

Ukupno, dobijeni rezultati se mogu smatrati dokazom delimične podudarnosti koncepata kompleksa kod S. Freuda i A. Adlera.

Značajno je da je između indikatora energije potiskivanja i indikatora intenziteta osjećaja vlastite nedostatnosti u uzorku u cjelini dobijena pozitivna linearna korelacija (p = +0,491, p<0,01). Как мы можем убедиться, применение критерия φ* позволяет проникнуть в более тонкие и содержательно значимые соотношения между этими двумя показателями.

Primjer 4 - korištenje φ* kriterija u kombinaciji s kriterijem λ Kolmogorov-Smirnov u cilju postizanja maksimuma precizanrezultat

Ako se uzorci uporede prema bilo kojim kvantitativno izmjerenim pokazateljima, nastaje problem identifikacije tačke distribucije koja se može koristiti kao kritična tačka u podjeli svih ispitanika na one koji „imaju učinak“ i one koji „nemaju učinak“.

U principu, tačka u kojoj bismo podijelili grupu na podgrupe gdje ima efekta i gdje nema efekta može se izabrati sasvim proizvoljno. Može nas zanimati bilo koji efekat i, stoga, možemo podijeliti oba uzorka na dva dijela u bilo kojem trenutku, sve dok to ima smisla.

Da bi se maksimizirala snaga φ* testa, međutim, potrebno je odabrati tačku u kojoj su razlike između dvije upoređene grupe najveće. Najtačnije, to možemo učiniti koristeći algoritam za izračunavanje kriterijaλ , što vam omogućava da otkrijete tačku maksimalnog odstupanja između dva uzorka.

Mogućnost kombinovanja kriterijuma φ* iλ opisao E.V. Gubler (1978, str. 85-88). Pokušajmo koristiti ovu metodu u rješavanju sljedećeg problema.

U zajedničkoj studiji M.A. Kuročkina, E.V. Sidorenko i Yu.A. Churakov (1992) u UK je sproveo istraživanje engleskih liječnika opće prakse u dvije kategorije: a) doktori koji su podržavali medicinsku reformu i koji su već pretvorili svoje prijemne kancelarije u organizacije koje drže fondove sa sopstvenim budžetom; b) ljekari čije ordinacije još uvijek nemaju vlastita sredstva iu cijelosti su obezbjeđene iz državnog budžeta. Upitnici su poslati uzorku od 200 ljekara, reprezentativnih za opštu populaciju engleskih ljekara u smislu zastupljenosti ljudi različitog pola, starosti, radnog staža i mjesta rada – u velikim gradovima ili u provincijama.

Na upitnik je odgovorilo 78 ljekara, od kojih je 50 radilo u čekaonicama sa sredstvima, a 28 iz čekaonica bez sredstava. Svaki od ljekara morao je predvidjeti koliki će biti udio prijema sa sredstvima u narednoj, 1993. godini. Na ovo pitanje odgovorilo je samo 70 ljekara od 78 koji su poslali odgovore. Distribucija njihovih prognoza prikazana je u tabeli. 5.8 posebno za grupu lekara sa sredstvima i grupu lekara bez sredstava.

Da li se prognoze lekara sa sredstvima i lekara bez sredstava po čemu razlikuju?

Tabela 5.8

Distribucija prognoza lekara opšte prakse o tome koliki će biti udeo urgentnih ambulanti sa sredstvima u 1993.

Predviđeno učešće
prijemne sobe sa sredstvima	doktori sa fondom (n 1 =45)	doktori bez fonda (n 2 =25)	Iznosi
1. od 0 do 20%	4	5	9
2. od 21 do 40%	15	I	26
3. od 41 do 60%	18	5	23
4. od 61 do 80%	7	4	I
5. od 81 do 100%	1	0	1
Iznosi	45	25	70

Odredimo tačku maksimalnog neslaganja između dvije distribucije odgovora koristeći algoritam 15 iz klauzule 4.3 (vidi tabelu 5.9).

Tabela 5.9

Proračun maksimalne razlike akumuliranih frekvencija u distribucijama prognoza ljekara dvije grupe

Predviđeni udio prijema sa sredstvima (%)	Empirijske frekvencije izbora za datu kategoriju odgovora		Empirijske frekvencije		Kumulativne empirijske frekvencije		razlika (d)
	doktori sa fondom(n 1 =45)	doktori bez fonda (n 2 =25)	f* uh 1	f* a2	∑f* e1	∑f* a1
1. od 0 do 20% 2. od 21 do 40% 3. od 41 do 60% 4. od 61 do 80% 5. od 81 do 100%	4 15 18 7 1	5 11 5 4 0	0,089 0,333 0,400 0,156 0,022	0,200 0,440 0,200 0,160 0	0,089 0,422 0,822 0,978 1,000	0,200 0,640 0,840 1,000 1,000	0111 0,218 0,018 0,022 0

Maksimalna otkrivena razlika između dvije akumulirane empirijske frekvencije je0,218.

Ispostavilo se da je ova razlika akumulirana u drugoj kategoriji prognoze. Pokušajmo upotrijebiti gornju granicu ove kategorije kao kriterij za podjelu oba uzorka na podgrupu u kojoj „postoji učinak“ i podgrupu u kojoj „nema efekta“. Pretpostavićemo da postoji „efekat“ ako određeni lekar predvidi od 41 do 100% prijema sa sredstvima u1993 godine, te da „nema efekta“ ako određeni ljekar predvidi od 0 do 40% prijema sa sredstvima u1993 godine. Kombiniramo kategorije prognoze 1 i 2 s jedne strane i kategorije prognoze 3, 4 i 5 s druge strane. Rezultirajuća distribucija prognoza prikazana je u tabeli. 5.10.

Tabela 5.10

Distribucija prognoza za ljekare sa sredstvima i ljekare bez sredstava

Predviđeni udio prijema sa sredstvima (%1	Empirijske frekvencije za odabir date kategorije prognoze		Iznosi
	doktori sa fondom(n 1 =45)	doktori bez fonda(n 2 =25)
1. od 0 do 40%	19	16	35
2. od 41 do 100%	26	9	35
Iznosi	45	25	70

Dobivenu tabelu (tabela 5.10) možemo koristiti za testiranje različitih hipoteza upoređivanjem bilo koje dvije njene ćelije. Setimo se da je ovo takozvana tabela sa četiri ćelije ili četiri polja.

Ovdje nas zanima da li ljekari koji već imaju sredstva predviđaju da će pokret u budućnosti biti veći od ljekara koji nemaju sredstava. Stoga, uslovno smatramo da „efekt postoji“ kada prognoza spada u kategoriju od 41 do 100%. Da bismo pojednostavili proračune, sada trebamo rotirati sto za 90°, rotirajući ga u smjeru kazaljke na satu. To možete učiniti čak i doslovno okretanjem knjige zajedno sa stolom. Sada možemo prijeći na radni list za izračunavanje φ* kriterija – Fisherova kutna transformacija.

Table 5.11

Tabela sa četiri ćelije za izračunavanje Fišerovog φ* kriterijuma za identifikaciju razlika u prognozama dve grupe lekara opšte prakse

Grupa	Postoji efekat - prognoza od 41 do 100%	Nema efekta - prognoza od 0 do 40%	Ukupno
Igrupa - doktori koji su uzimali fond	26 (57.8%)	19 (42.2%)	45
IIgrupa - doktori koji nisu uzimali fond	9 (36.0%)	16 (64.0%)	25
Ukupno	35	35	70

Hajde da formulišemo hipoteze.

H 0 : Proporcija osobapredviđajući širenje sredstava na 41%-100% svih ljekarskih ordinacija, u grupi ljekara sa sredstvima nema više nego u grupi ljekara bez sredstava.

H 1 : Udio ljudi koji predviđaju širenje sredstava na 41%-100% svih prijema veći je u grupi ljekara sa sredstvima nego u grupi ljekara bez sredstava.

Određivanje vrijednosti φ 1 i φ 2 prema tabeliXIIDodatak 1. Podsjetimo da je φ 1 je uvijek ugao koji odgovara većem procentu.

Sada odredimo empirijsku vrijednost kriterija φ*:

Prema tabeli.XIIIU Dodatku 1 utvrđujemo kojem nivou značajnosti ova vrijednost odgovara: p = 0,039.

Koristeći istu tablicu u Dodatku 1, možete odrediti kritične vrijednosti kriterija φ*:

odgovor: Ali je odbijen (p=0,039). Udio ljudi koji predviđaju širenje sredstava na41-100 % svih prijema u grupi ljekara koji su uzimali fond prelazi ovaj udio u grupi ljekara koji nisu uzimali fond.

Drugim riječima, liječnici koji već rade u svojim čekaonicama na posebnom budžetu predviđaju ove godine šire širenje ove prakse od ljekara koji još nisu pristali da pređu na samostalni budžet. Postoji više tumačenja ovog rezultata. Na primjer, može se pretpostaviti da ljekari u svakoj grupi podsvjesno smatraju svoje ponašanje tipičnijim. To također može značiti da ljekari koji su već usvojili samofinansiranje imaju tendenciju da preuveličaju obim ovog pokreta, jer treba da opravdaju svoju odluku. Identificirane razlike mogu značiti i nešto što je potpuno izvan okvira pitanja koja se postavljaju u studiji. Na primjer, da aktivnost ljekara koji rade na nezavisnom budžetu doprinosi zaoštravanju razlika u stavovima obje grupe. Bili su aktivniji kada su pristali da uzmu sredstva bili su aktivniji kada su se potrudili da odgovore na upitnik putem pošte; aktivniji su kada predviđaju da će drugi ljekari biti aktivniji u primanju sredstava.

Na ovaj ili onaj način, možemo biti sigurni da je otkriveni nivo statističkih razlika maksimalno mogući za ove stvarne podatke. Utvrdili smo koristeći kriterijumλ tačka maksimalne divergencije između dve distribucije, iu toj tački su uzorci podeljeni na dva dela.

Vaša ocjena.