Binomna distribucija. Diskretne distribucije u MS EXCEL-u
Binomna distribucija- jedna od najvažnijih distribucija vjerovatnoće diskretne promjene slučajna varijabla. Binomna distribucija je raspodjela vjerovatnoće nekog broja m događaj A V n međusobno nezavisna zapažanja. Često događaj A naziva "uspjeh" posmatranja, a suprotan događaj - "neuspjeh", ali je ova oznaka vrlo uslovna.
Uvjeti binomne distribucije:
- izvršeno ukupno n suđenja u kojima je događaj A može se dogoditi ili ne mora;
- događaj A u svakom od pokusa može se dogoditi sa istom vjerovatnoćom str;
- testovi su međusobno nezavisni.
Verovatnoća da u n test događaj A upravo m puta, može se izračunati korištenjem Bernoullijeve formule:
![]()
![]() ,
,
Gdje str- vjerovatnoća da će se događaj dogoditi A;
q = 1 - str je vjerovatnoća da se dogodi suprotan događaj.
Hajde da to shvatimo zašto je binomna distribucija povezana sa Bernulijevom formulom na gore opisan način . Događaj - broj uspjeha na n testovi su podijeljeni na više opcija, u svakoj od kojih se postiže uspjeh u m iskušenja, a neuspjeh - u n - m testovi. Razmotrite jednu od ovih opcija - B1 . Prema pravilu sabiranja vjerovatnoća, množimo vjerovatnoće suprotnih događaja:
![]() ,
,
i ako označimo q = 1 - str, To
![]() .
.
Istu vjerovatnoću imat će bilo koja druga opcija u kojoj m uspjeh i n - m neuspjesi. Broj takvih opcija jednak je broju načina na koje je to moguće n test get m uspjeh.
Zbir vjerovatnoća svih m broj događaja A(brojevi od 0 do n) je jednako jedan:
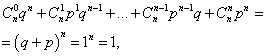
gdje je svaki član član Njutnovog binoma. Stoga se razmatrana raspodjela naziva binomna distribucija.
U praksi je često potrebno izračunati vjerovatnoće „najviše m uspjeh u n testovi" ili "barem m uspjeh u n testovi". Za to se koriste sljedeće formule.
Integralna funkcija, tj vjerovatnoća F(m) to u n događaj posmatranja A više neće doći m jednom, može se izračunati pomoću formule:
Zauzvrat vjerovatnoća F(≥m) to u n događaj posmatranja A dođi barem m jednom, izračunava se po formuli:
Ponekad je zgodnije izračunati vjerovatnoću da in n događaj posmatranja A više neće doći m puta, kroz vjerovatnoću suprotnog događaja:
![]() .
.
Koju od formula koristiti ovisi o tome koja od njih sadrži manje pojmova.
Karakteristike binomne distribucije se izračunavaju korištenjem sljedećih formula .
Očekivana vrijednost: .
disperzija: .
Standardna devijacija: .
Binomna distribucija i proračuni u MS Excel-u
Vjerojatnost binomne distribucije P n ( m) i vrijednost integralne funkcije F(m) može se izračunati pomoću MS Excel funkcije BINOM.DIST. Prozor za odgovarajući proračun je prikazan ispod (kliknite levi taster miša za uvećanje).

MS Excel zahtijeva da unesete sljedeće podatke:
- broj uspjeha;
- broj testova;
- vjerovatnoća uspjeha;
- integral - logička vrijednost: 0 - ako treba izračunati vjerovatnoću P n ( m) i 1 - ako je vjerovatnoća F(m).
Primjer 1 Direktor kompanije sumirao je podatke o broju prodatih kamera u proteklih 100 dana. U tabeli su sumirane informacije i izračunate vjerovatnoće da će se određeni broj kamera dnevno prodati.
Dan završava profitom ako se proda 13 ili više kamera. Verovatnoća da će dan biti odrađen sa profitom:
![]()
Vjerovatnoća da će dan biti odrađen bez dobiti:
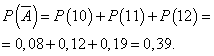
Neka je vjerovatnoća da je dan odrađen sa profitom konstantna i jednaka 0,61, a broj prodatih kamera dnevno ne ovisi o danu. Tada možete koristiti binomnu distribuciju, gdje je događaj A- dan će biti odrađen sa profitom, - bez dobiti.
Verovatnoća da će od 6 dana sve biti rešeno sa profitom:
![]() .
.
Isti rezultat dobijamo koristeći MS Excel funkciju BINOM.DIST (vrijednost integralne vrijednosti je 0):
P 6 (6 ) = BINOM.DIST(6; 6; 0,61; 0) = 0,052.
Verovatnoća da će od 6 dana 4 ili više dana biti odrađeno sa profitom:
Gdje ![]() ,
,
![]() ,
,
Koristeći MS Excel funkciju BINOM.DIST, izračunavamo vjerovatnoću da od 6 dana ne više od 3 dana bude završeno sa profitom (vrijednost integralne vrijednosti je 1):
P 6 (≤3 ) = BINOM.DIST(3, 6, 0,61, 1) = 0,435.
Verovatnoća da će od 6 dana sve biti rešeno sa gubicima:
![]() ,
,
Isti indikator izračunavamo koristeći MS Excel funkciju BINOM.DIST:
P 6 (0 ) = BINOM.DIST(0; 6; 0,61; 0) = 0,0035.
Riješite problem sami, a zatim pogledajte rješenje
Primjer 2 Urna sadrži 2 bijele kugle i 3 crne. Iz urne se vadi kugla, postavlja se boja i vraća nazad. Pokušaj se ponavlja 5 puta. Broj pojavljivanja bijelih kuglica je diskretna slučajna varijabla X, distribuiran prema binomskom zakonu. Sastavite zakon raspodjele slučajne varijable. Definišite modu očekivanu vrijednost i disperzija.
Nastavljamo da zajedno rješavamo probleme
Primjer 3 Od kurirske službe otišao do objekata n= 5 kurira. Svaki kurir sa vjerovatnoćom str= 0,3 kasni za objekat bez obzira na ostale. Diskretna slučajna varijabla X- broj kasnih kurira. Konstruirajte seriju distribucije ove slučajne varijable. Pronađite njegovo matematičko očekivanje, varijansu, standardnu devijaciju. Pronađite vjerovatnoću da će najmanje dva kurira zakasniti na objekte.
Razmotrite binomnu distribuciju, izračunajte njeno matematičko očekivanje, varijansu, mod. Koristeći MS EXCEL funkciju BINOM.DIST(), nacrtat ćemo grafove funkcije distribucije i gustine vjerovatnoće. Procijenimo parametar distribucije p, matematičko očekivanje distribucije i standardnu devijaciju. Uzmite u obzir i Bernoullijevu distribuciju.
Definicija. Neka se drže n testovi, u svakom od kojih se mogu pojaviti samo 2 događaja: događaj "uspjeh" s vjerovatnoćom str ili događaj "neuspjeh" s vjerovatnoćom q =1-p (tzv Bernoullijeva šema,Bernoullisuđenja).
Verovatnoća dobijanja tačno x uspjeh u ovim n testovi je jednak:
Broj uspjeha u uzorku x je slučajna varijabla koja ima Binomna distribucija(engleski) Binomdistribucija) str I n– su parametri ove distribucije.
Podsjetite to kako biste se prijavili Bernoullijeve šeme i shodno tome binomna distribucija, moraju biti ispunjeni sljedeći uslovi:
- svako ispitivanje mora imati tačno dva ishoda, uslovno nazvana "uspjeh" i "neuspjeh".
- rezultat svakog testa ne treba da zavisi od rezultata prethodnih testova (nezavisnost testa).
- stopa uspjeha str treba biti konstantan za sve testove.
Binomna distribucija u MS EXCEL-u
U MS EXCEL-u, počevši od verzije 2010, za Binomna distribucija postoji funkcija BINOM.DIST() , engleski naziv- BINOM.DIST(), koji vam omogućava da izračunate vjerovatnoću da će uzorak biti tačan X"uspjesi" (tj. funkcija gustoće vjerovatnoće p(x), vidi gornju formulu) i integralna funkcija distribucije(vjerovatnoća da će uzorak imati x ili manje "uspjeha", uključujući 0).
Prije MS EXCEL 2010, EXCEL je imao funkciju BINOMDIST(), koja vam također omogućava da izračunate funkcija distribucije I gustina vjerovatnoće p(x). BINOMDIST() je ostavljen u MS EXCEL 2010 radi kompatibilnosti.
Datoteka primjera sadrži grafikone gustina raspodjele vjerovatnoće I .

Binomna distribucija ima oznaku B(n; str) .
Bilješka: Za gradnju integralna funkcija distribucije tip grafikona savršenog uklapanja Raspored, Za gustina distribucije – Histogram sa grupisanjem. Za više informacija o građenju dijagrama, pročitajte članak Glavne vrste dijagrama.
Bilješka: Za praktičnost pisanja formula u datoteku primjera, kreirana su imena za parametre Binomna distribucija: n i str.

Datoteka primjera prikazuje različite izračune vjerovatnoće pomoću MS EXCEL funkcija:

Kao što se vidi na gornjoj slici, pretpostavlja se da:
- Beskonačna populacija od koje je napravljen uzorak sadrži 10% (ili 0,1) dobrih elemenata (parametar str, treći argument funkcije =BINOM.DIST() )
- Za izračunavanje vjerovatnoće da će u uzorku od 10 elemenata (parametar n, drugi argument funkcije) bit će točno 5 valjanih elemenata (prvi argument), potrebno je napisati formulu: =BINOM.DIST(5, 10, 0.1, FALSE)
- Poslednji, četvrti element je postavljen = FALSE, tj. vrijednost funkcije se vraća gustina distribucije.
Ako je vrijednost četvrtog argumenta TRUE, tada funkcija BINOM.DIST() vraća vrijednost integralna funkcija distribucije ili jednostavno funkcija distribucije. U ovom slučaju možete izračunati vjerovatnoću da će broj dobrih stavki u uzorku biti iz određenog raspona, na primjer, 2 ili manje (uključujući 0).
Da biste to učinili, morate napisati formulu:
= BINOM.DIST(2, 10, 0,1, TRUE)
Bilješka: Za necijelobrojnu vrijednost x, . Na primjer, sljedeće formule će vratiti istu vrijednost:
=BINOM.DIST( 2
; 10; 0,1; ISTINITO)
=BINOM.DIST( 2,9
; 10; 0,1; ISTINITO)
Bilješka: U primjeru datoteke gustina vjerovatnoće I funkcija distribucije također se izračunava korištenjem definicije i funkcije COMBIN().
Pokazatelji distribucije
IN primjer datoteke na listu Primjer postoje formule za izračunavanje nekih indikatora distribucije:
- =n*p;
- (kvadrat standardne devijacije) = n*p*(1-p);
- = (n+1)*p;
- =(1-2*p)*ROOT(n*p*(1-p)).
Izvodimo formulu matematičko očekivanje Binomna distribucija koristeći Bernoullijeva šema.
Po definiciji, slučajna varijabla X in Bernoullijeva šema(Bernoullijeva slučajna varijabla) ima funkcija distribucije:

Ova distribucija se zove Bernulijeva distribucija.
Bilješka: Bernulijeva distribucija- poseban slučaj Binomna distribucija sa parametrom n=1.
Hajde da generišemo 3 niza od 100 brojeva sa različitim verovatnoćama uspeha: 0,1; 0,5 i 0,9. Da biste to učinili, u prozoru Generisanje slučajnih brojeva postavite sljedeće parametre za svaku vjerovatnoću p:

Bilješka: Ako postavite opciju Slučajno rasipanje (Slučajno sjeme), tada možete odabrati određeni nasumični skup generiranih brojeva. Na primjer, postavljanjem ove opcije =25, možete generirati iste skupove slučajnih brojeva na različitim računarima (ako su, naravno, drugi parametri distribucije isti). Vrijednost opcije može imati cjelobrojne vrijednosti od 1 do 32 767. Naziv opcije Slučajno rasipanje može zbuniti. Bilo bi bolje da se to prevede kao Postavite broj sa slučajnim brojevima.
Kao rezultat, imaćemo 3 kolone od 100 brojeva, na osnovu kojih, na primjer, možemo procijeniti vjerovatnoću uspjeha str prema formuli: Broj uspjeha/100(cm. primjer lista datoteka Generiranje Bernoullija).

Bilješka: Za Bernoullijeve distribucije sa p=0,5, možete koristiti formulu =RANDBETWEEN(0;1) , što odgovara .
Generisanje slučajnih brojeva. Binomna distribucija
Pretpostavimo da u uzorku ima 7 neispravnih predmeta. To znači da je "vrlo vjerovatno" da se udio neispravnih proizvoda promijenio. str, što je karakteristika našeg proizvodnog procesa. Iako je ova situacija “vrlo vjerovatna”, postoji mogućnost (alfa rizik, greška tipa 1, “lažni alarm”) da str je ostao nepromijenjen, a povećan broj neispravnih proizvoda uzrokovan je slučajnim uzorkovanjem.
Kao što se može vidjeti na donjoj slici, 7 je broj neispravnih proizvoda koji je prihvatljiv za proces sa p=0,21 pri istoj vrijednosti Alpha. Ovo ilustruje da kada se prekorači prag neispravnih predmeta u uzorku, str“vjerovatno” povećao. Izraz "najvjerovatnije" znači da postoji samo 10% šanse (100%-90%) da je odstupanje procenta neispravnih proizvoda iznad praga posljedica samo slučajnih uzroka.

Dakle, prekoračenje graničnog broja neispravnih proizvoda u uzorku može poslužiti kao signal da se proces poremetio i počeo proizvoditi b O veći procenat neispravnih proizvoda.
Bilješka: Prije MS EXCEL 2010, EXCEL je imao funkciju CRITBINOM() , koja je ekvivalentna BINOM.INV() . CRITBINOM() je ostavljen u MS EXCEL 2010 i novijim radi kompatibilnosti.
Odnos binomske distribucije prema drugim distribucijama
Ako je parametar n Binomna distribucija teži beskonačnosti i str teži 0, tada u ovom slučaju Binomna distribucija može se aproksimirati.
Moguće je formulisati uslove kada je aproksimacija Poissonova distribucija radi dobro:
- str<0,1 (što manje str i više n, što je tačnija aproksimacija);
- str>0,9 (s obzirom na to q=1- str, proračuni u ovom slučaju moraju se izvršiti pomoću q(A X potrebno je zamijeniti sa n- x). Dakle, što manje q i više n, to je tačnija aproksimacija).
Na 0,1<=p<=0,9 и n*p>10 Binomna distribucija može se aproksimirati.
sa svoje strane, Binomna distribucija može poslužiti kao dobra aproksimacija kada je veličina populacije N Hipergeometrijska distribucija mnogo veći od veličine uzorka n (tj. N>>n ili n/N<<1).
Više o odnosu gore navedenih distribucija možete pročitati u članku. Navedeni su i primjeri aproksimacije, te su objašnjeni uslovi kada je to moguće i sa kojom tačnošću.
SAVJET: O ostalim distribucijama MS EXCEL-a možete pročitati u članku.
Za razliku od normalne i uniformne distribucije, koje opisuju ponašanje varijable u uzorku ispitanika, binomna distribucija se koristi u druge svrhe. Služi za predviđanje vjerovatnoće dva međusobno isključiva događaja u određenom broju nezavisnih ispitivanja. Klasičan primjer binomne distribucije je bacanje novčića koji padne na tvrdu površinu. Dva ishoda (događaja) su podjednako vjerovatna: 1) novčić padne „orao“ (vjerovatnoća je jednaka R) ili 2) novčić padne „repovi“ (vjerovatnoća je jednaka q). Ako se ne dobije treći ishod, onda str = q= 0,5 i str + q= 1. Koristeći formulu binomne raspodjele, možete odrediti, na primjer, kolika je vjerovatnoća da u 50 pokušaja (broj bacanja novčića) posljednji padne glavom, recimo, 25 puta.
Za dalje razmišljanje uvodimo opšteprihvaćenu notaciju:
n je ukupan broj zapažanja;
i- broj događaja (ishoda) koji nas zanimaju;
n – i– broj alternativnih događaja;
str- empirijski utvrđena (ponekad - pretpostavljena) vjerovatnoća događaja od interesa za nas;
q je vjerovatnoća alternativnog događaja;
P n ( i) je predviđena vjerovatnoća događaja koji nas zanima i za određeni broj zapažanja n.
Formula binomne distribucije:
U slučaju jednako vjerovatnog ishoda događaja ( p = q) možete koristiti pojednostavljenu formulu:
![]() (6.8)
(6.8)
Razmotrimo tri primjera koji ilustruju upotrebu formula binomne distribucije u psihološkim istraživanjima.
Primjer 1
Pretpostavimo da 3 učenika rješavaju problem povećane složenosti. Za svaki od njih podjednako su vjerovatna 2 ishoda: (+) - rješenje i (-) - nerješenje problema. Ukupno je moguće 8 različitih ishoda (2 3 = 8).
Vjerovatnoća da se nijedan učenik neće nositi sa zadatkom je 1/8 (opcija 8); 1 učenik će završiti zadatak: P= 3/8 (opcije 4, 6, 7); 2 učenika - P= 3/8 (opcije 2, 3, 5) i 3 učenika – P=1/8 (opcija 1).
Potrebno je odrediti vjerovatnoću da će tri od 5 učenika uspješno izaći na kraj sa ovim zadatkom.
Rješenje
Ukupni mogući ishodi: 2 5 = 32.
Ukupan broj opcija 3(+) i 2(-) je

Stoga je vjerovatnoća očekivanog ishoda 10/32 » 0,31.
Primjer 3
Vježbajte
Odredite vjerovatnoću da će se 5 ekstroverta naći u grupi od 10 nasumičnih ispitanika.
Rješenje
1. Unesite notaciju: p=q= 0,5; n= 10; i = 5; P 10 (5) = ?
2. Koristimo pojednostavljenu formulu (vidi gore):
Zaključak
Vjerovatnoća da će se među 10 nasumičnih ispitanika naći 5 ekstroverta je 0,246.
Bilješke
1. Proračun po formuli s dovoljno velikim brojem pokušaja je prilično naporan, stoga se u ovim slučajevima preporučuje korištenje tablica binomne distribucije.
2. U nekim slučajevima, vrijednosti str I q može se postaviti na početku, ali ne uvijek. U pravilu se izračunavaju na osnovu rezultata preliminarnih ispitivanja (pilot studija).
3. Na grafičkoj slici (u koordinatama P n(i) = f(i)) binomna distribucija može imati različite oblike: u slučaju p = q raspodjela je simetrična i podsjeća na Gaussovu normalnu raspodjelu; asimetrija distribucije je veća, što je veća razlika između vjerovatnoća str I q.
Poissonova distribucija
Poissonova raspodjela je poseban slučaj binomne distribucije, koja se koristi kada je vjerovatnoća događaja od interesa vrlo niska. Drugim riječima, ova distribucija opisuje vjerovatnoću retkih događaja. Poissonova formula se može koristiti za str < 0,01 и q ≥ 0,99.
Poissonova jednadžba je približna i opisana je sljedećom formulom:
![]() (6.9)
(6.9)
gdje je μ proizvod prosječne vjerovatnoće događaja i broja zapažanja.
Kao primjer, razmotrite algoritam za rješavanje sljedećeg problema.
Zadatak
Nekoliko godina u 21 velikoj klinici u Rusiji vršeno je masovno ispitivanje novorođenčadi na bolest dojenčadi sa Daunovom bolešću (uzorak je u prosjeku bio 1000 novorođenčadi u svakoj klinici). Primljeni su sljedeći podaci:
Vježbajte
1. Odrediti prosječnu vjerovatnoću bolesti (u smislu broja novorođenčadi).
2. Odrediti prosječan broj novorođenčadi sa jednom bolešću.
3. Odrediti vjerovatnoću da će među 100 nasumično odabranih novorođenčadi biti 2 bebe sa Daunovom bolešću.
Rješenje
1. Odredite prosječnu vjerovatnoću bolesti. Pri tome moramo se rukovoditi sljedećim obrazloženjem. Daunova bolest je registrovana samo u 10 od 21 klinike.U 11 ambulanti nije bilo nikakvih bolesti, u 6 klinika registrovan je 1 slučaj, u 2 ambulante 2 slučaja, u 1. ambulanti 3 i u 1. klinici 4 slučaja. 5 slučajeva nije pronađeno ni u jednoj klinici. Da bi se odredila prosječna vjerovatnoća bolesti, potrebno je ukupan broj slučajeva (6 1 + 2 2 + 1 3 + 1 4 = 17) podijeliti sa ukupnim brojem novorođenčadi (21000):
![]()
2. Broj novorođenčadi koja predstavlja jednu bolest recipročan je prosječnoj vjerovatnoći, odnosno jednak je ukupnom broju novorođenčadi podijeljen sa brojem registrovanih slučajeva:
![]()
3. Zamijenite vrijednosti str = 0,00081, n= 100 i i= 2 u Poissonovu formulu:
Odgovori
Vjerovatnoća da će se među 100 slučajno odabranih novorođenčadi naći 2 novorođenčadi sa Daunovom bolešću je 0,003 (0,3%).
Povezani zadaci
Zadatak 6.1
Vježbajte
Koristeći podatke problema 5.1 o vremenu senzomotorne reakcije, izračunajte asimetriju i eksces distribucije VR.
Zadatak 6. 2
200 diplomiranih studenata testirano je na nivo inteligencije ( IQ). Nakon normalizacije rezultirajuće raspodjele IQ prema standardnoj devijaciji dobijeni su sljedeći rezultati:
Vježbajte
Koristeći Kolmogorov i hi-kvadrat test, utvrdite da li rezultirajuća distribucija indikatora odgovara IQ normalno.
Zadatak 6. 3
Kod odraslog ispitanika (muškarac od 25 godina) proučavano je vrijeme jednostavne senzomotorne reakcije (SR) kao odgovor na zvučni stimulans konstantne frekvencije od 1 kHz i intenziteta od 40 dB. Stimulus je predstavljen sto puta u intervalima od 3-5 sekundi. Pojedinačne VR vrijednosti za 100 ponavljanja raspoređene su na sljedeći način:
Vježbajte
1. Konstruisati histogram frekvencije distribucije VR; odrediti prosječnu vrijednost VR i vrijednost standardne devijacije.
2. Izračunati koeficijent asimetrije i kurtozis distribucije BP; na osnovu primljenih vrednosti As I Pr donijeti zaključak o usklađenosti ili neusklađenosti ove distribucije sa normalnom.
Zadatak 6.4
Godine 1998. 14 osoba (5 dječaka i 9 djevojčica) završilo je škole u Nižnjem Tagilu sa zlatnim medaljama, 26 osoba (8 dječaka i 18 djevojčica) sa srebrnim medaljama.
Pitanje
Može li se reći da djevojčice češće dobijaju medalje od dječaka?
Bilješka
Odnos broja dječaka i djevojčica u opštoj populaciji smatra se jednakim.
Zadatak 6.5
Smatra se da je broj ekstrovertnih i introvertnih u homogenoj grupi ispitanika približno isti.
Vježbajte
Odredite vjerovatnoću da će se u grupi od 10 nasumično odabranih subjekata naći 0, 1, 2, ..., 10 ekstroverta. Konstruirajte grafički izraz za distribuciju vjerovatnoće nalaženja 0, 1, 2, ..., 10 ekstroverta u datoj grupi.
Zadatak 6.6
Vježbajte
Izračunaj vjerovatnoću P n(i) funkcije binomne distribucije za str= 0,3 i q= 0,7 za vrijednosti n= 5 i i= 0, 1, 2, ..., 5. Konstruisati grafički izraz zavisnosti P n(i) = f(i) .
Zadatak 6.7
Posljednjih godina se među određenim dijelom populacije ustalilo vjerovanje u astrološke prognoze. Prema rezultatima preliminarnih istraživanja, utvrđeno je da oko 15% stanovništva vjeruje u astrologiju.
Vježbajte
Odredite vjerovatnoću da će među 10 nasumično odabranih ispitanika biti 1, 2 ili 3 osobe koje vjeruju u astrološke prognoze.
Zadatak 6.8
Zadatak
U 42 srednje škole u gradu Jekaterinburgu i Sverdlovskoj oblasti (ukupan broj učenika je 12.260), tokom nekoliko godina otkriven je sljedeći broj slučajeva mentalnih bolesti među učenicima:
Vježbajte
Neka se nasumično ispita 1000 školaraca. Izračunajte kolika je vjerovatnoća da će se među ovim hiljadu školaraca identificirati 1, 2 ili 3 psihički bolesne djece?
ODJELJAK 7. MJERE RAZLIKE
Formulacija problema
Pretpostavimo da imamo dva nezavisna uzorka subjekata X I at. Nezavisna uzorci se broje kada se isti subjekt (subjekat) pojavljuje samo u jednom uzorku. Zadatak je da se ti uzorci (dva skupa varijabli) međusobno uporede zbog njihovih razlika. Naravno, bez obzira koliko su bliske vrijednosti varijabli u prvom i drugom uzorku, neke, čak i beznačajne, razlike između njih će se otkriti. Sa stanovišta matematičke statistike, zanima nas pitanje da li su razlike između ovih uzoraka statistički značajne (statistički značajne) ili nepouzdane (slučajne).
Najčešći kriterijumi za značajnost razlika između uzoraka su parametarske mere razlika - Studentov kriterijum I Fišerov kriterijum. U nekim slučajevima se koriste neparametarski kriterijumi - Rosenbaum Q test, Mann-Whitney U test i drugi. Fisher kutna transformacija φ*, koji vam omogućavaju da međusobno uporedite vrijednosti izražene kao postoci (procenti). I, konačno, kao poseban slučaj, za poređenje uzoraka mogu se koristiti kriterijumi koji karakterišu oblik distribucije uzoraka - kriterijum χ 2 Pearson I kriterij λ Kolmogorov – Smirnov.
Kako bismo bolje razumjeli ovu temu, postupit ćemo na sljedeći način. Isti problem ćemo riješiti sa četiri metode koristeći četiri različita kriterija - Rosenbaum, Mann-Whitney, Student i Fisher.
Zadatak
30 učenika (14 dječaka i 16 djevojčica) tokom ispitne sesije testirano je Spielbergerovim testom na nivo reaktivne anksioznosti. Dobijeni su sljedeći rezultati (tabela 7.1):
Tabela 7.1
| Subjekti | Nivo reaktivne anksioznosti | |||||||||||||||
| Mladi | ||||||||||||||||
| cure |
Vježbajte
Utvrditi da li su razlike u nivou reaktivne anksioznosti kod dječaka i djevojčica statistički značajne.
Čini se da je zadatak prilično tipičan za psihologa specijaliziranog za područje obrazovne psihologije: ko akutnije doživljava ispitni stres - dječaci ili djevojčice? Ako su razlike između uzoraka statistički značajne, onda u ovom aspektu postoje značajne rodne razlike; ako su razlike slučajne (ne statistički značajne), ovu pretpostavku treba odbaciti.
7. 2. Neparametarski test Q Rosenbaum
Q-Rozenbaumov kriterijum se zasniva na poređenju "superimponovanih" jedna na drugu rangiranih serija vrednosti dve nezavisne varijable. Istovremeno, priroda distribucije osobine unutar svakog reda se ne analizira – u ovom slučaju je bitna samo širina nepreklapajućih dijelova dva rangirana reda. Kada se međusobno porede dve rangirane serije varijabli, moguće su 3 opcije:
1. rangirani činovi x I y nemaju područje preklapanja, tj. sve vrijednosti prve rangirane serije ( x) je veći od svih vrijednosti drugorangirane serije ( y):
U ovom slučaju, razlike između uzoraka, određene bilo kojim statističkim kriterijumom, svakako su značajne, a upotreba Rozenbaumovog kriterijuma nije potrebna. Međutim, u praksi je ova opcija izuzetno rijetka.
2. Rangirani redovi se potpuno međusobno preklapaju (po pravilu je jedan red unutar drugog), nema zona koje se ne preklapaju. U ovom slučaju, Rosenbaumov kriterij nije primjenjiv.

3. Postoji područje preklapanja redova, kao i dva područja koja se ne preklapaju ( N 1 I N 2) vezano za drugačije rangirane serije (označavamo X- red pomaknut prema velikom, y- u smjeru nižih vrijednosti):

Ovaj slučaj je tipičan za korištenje Rosenbaumovog kriterija, pri korištenju kojeg se moraju poštovati sljedeći uvjeti:
1. Volumen svakog uzorka mora biti najmanje 11.
2. Veličine uzoraka ne bi se trebale značajno razlikovati jedna od druge.
Kriterijum Q Rosenbaum odgovara broju vrijednosti koje se ne preklapaju: Q = N 1 +N 2 . Zaključak o pouzdanosti razlika između uzoraka donosi se ako Q > Q kr . Istovremeno, vrijednosti Q cr su u posebnim tabelama (vidi Dodatak, Tabela VIII).
Vratimo se našem zadatku. Hajde da uvedemo notaciju: X- izbor devojaka, y- Izbor momaka. Za svaki uzorak gradimo rangiranu seriju:
X: 28 30 34 34 35 36 37 39 40 41 42 42 43 44 45 46
y: 26 28 32 32 33 34 35 38 39 40 41 42 43 44
Brojimo broj vrijednosti u područjima rangirane serije koja se ne preklapaju. Zaredom X vrijednosti 45 i 46 se ne preklapaju, tj. N 1 = 2; u nizu y samo 1 vrijednost koja se ne preklapa 26 tj. N 2 = 1. Dakle, Q = N 1 +N 2 = 1 + 2 = 3.
U tabeli. VIII Dodatak nalazimo da Q kr . = 7 (za nivo značajnosti od 0,95) i Q cr = 9 (za nivo značajnosti od 0,99).
Zaključak
Zbog Q<Q cr, onda prema Rozenbaumovom kriterijumu razlike između uzoraka nisu statistički značajne.
Bilješka
Rosenbaumov test se može koristiti bez obzira na prirodu distribucije varijabli, odnosno u ovom slučaju nema potrebe za korištenjem Pearsonovog χ 2 i Kolmogorovljevog λ testa za određivanje vrste distribucije u oba uzorka.
7. 3. U-Mann-Whitney test
Za razliku od Rozenbaumovog kriterijuma, U Mann-Whitney test se zasniva na određivanju zone preklapanja između dva rangirana reda, tj. što je zona preklapanja manja, to su razlike između uzoraka značajnije. Za to se koristi posebna procedura za pretvaranje intervalnih skala u rangove.
Razmotrimo algoritam proračuna za U-kriterijum na primjeru prethodnog zadatka.
Tabela 7.2
| x, y | R xy | R xy * | R x | R y |
| 26 28 32 32 33 34 35 38 39 40 41 42 43 44 | 2,5 2,5 5,5 5,5 11,5 11,5 16,5 16,5 18,5 18,5 20,5 20,5 25,5 25,5 27,5 27,5 | 2,5 11,5 16,5 18,5 20,5 25,5 27,5 | 1 2,5 5,5 5,5 7 9 11,5 15 16,5 18,5 20,5 23 25,5 27,5 | |
| Σ | 276,5 | 188,5 |
1. Izrađujemo jednu rangiranu seriju od dva nezavisna uzorka. U ovom slučaju, vrijednosti za oba uzorka su pomiješane, kolona 1 ( x, y). Kako bi se pojednostavio daljnji rad (uključujući i kompjutersku verziju), vrijednosti za različite uzorke trebale bi biti označene različitim fontovima (ili različitim bojama), uzimajući u obzir činjenicu da ćemo ih u budućnosti objavljivati u različitim stupcima.
2. Transformirajte intervalnu skalu vrijednosti u ordinalnu (da bismo to učinili, sve vrijednosti ponovo označavamo brojevima ranga od 1 do 30, kolona 2 ( R xy)).
3. Uvodimo ispravke za povezane rangove (iste vrijednosti varijable su označene istim rangom, pod uslovom da se zbir rangova ne mijenja, kolona 3 ( R xy *). U ovoj fazi preporučuje se izračunavanje zbira rangova u 2. i 3. koloni (ako su sve ispravke tačne, onda bi ti sumi trebali biti jednaki).
4. Raspoređujemo brojeve rangova u skladu sa njihovom pripadnosti određenom uzorku (kolone 4 i 5 ( R x i R y)).
5. Izračunavanje vršimo prema formuli:
![]() (7.1)
(7.1)
Gdje T x je najveći od zbroja rangova ; n x i n y , odnosno veličine uzorka. U ovom slučaju, imajte na umu da ako T x< T y , zatim zapis x I y treba obrnuti.
6. Uporedi dobijenu vrijednost sa tabelarnom (vidi priloge, tabela IX) Zaključak o pouzdanosti razlika između dva uzorka donosi se ako U exp.< U cr. .
U našem primjeru ![]() U exp. = 83,5 > U cr. = 71.
U exp. = 83,5 > U cr. = 71.
Zaključak
Razlike između dva uzorka prema Mann-Whitney testu nisu statistički značajne.
Bilješke
1. Mann-Whitney test praktički nema ograničenja; minimalne veličine upoređenih uzoraka su 2 i 5 osoba (vidi tabelu IX u Dodatku).
2. Slično Rosenbaum testu, Mann-Whitney test se može koristiti za bilo koje uzorke, bez obzira na prirodu distribucije.
Studentov kriterijum
Za razliku od Rosenbaumovog i Mann-Whitneyjevog kriterija, kriterij t Studentova metoda je parametarska, odnosno zasniva se na određivanju glavnih statističkih pokazatelja – prosječnih vrijednosti u svakom uzorku ( i ) i njihovih varijansi (s 2 x i s 2 y), izračunatih pomoću standardnih formula (vidi Odjeljak 5).
Upotreba studentovog kriterijuma podrazumeva sledeće uslove:
1. Raspodjele vrijednosti za oba uzorka moraju biti u skladu sa zakonom normalna distribucija(vidi odjeljak 6).
2. Ukupna zapremina uzoraka mora biti najmanje 30 (za β 1 = 0,95) i najmanje 100 (za β 2 = 0,99).
3. Zapremine dva uzorka ne bi trebalo da se značajno razlikuju jedna od druge (ne više od 1,5 ÷ 2 puta).
Ideja Studentovog kriterija je prilično jednostavna. Pretpostavimo da su vrijednosti varijabli u svakom od uzoraka raspoređene prema normalnom zakonu, odnosno da imamo posla s dvije normalne distribucije koje se međusobno razlikuju po srednjim vrijednostima i varijansi (odnosno, i , i , vidi sliku 7.1).

s x s y
Rice. 7.1. Procjena razlika između dva nezavisna uzorka: i - srednje vrijednosti uzoraka x I y; s x i s y - standardne devijacije
Lako je razumjeti da će razlike između dva uzorka biti veće, što je veća razlika između srednjih vrijednosti i što su njihove varijanse (ili standardne devijacije) manje.
U slučaju nezavisnih uzoraka, Studentov koeficijent se određuje po formuli:
 (7.2)
(7.2)
Gdje n x i n y - broj uzoraka x I y.
Nakon izračunavanja Studentovog koeficijenta u tabeli standardnih (kritičnih) vrednosti t(vidi Dodatak, Tabela X) pronaći vrijednost koja odgovara broju stupnjeva slobode n = n x + n y - 2, i uporedi ga sa onim izračunatim po formuli. Ako t exp. £ t cr. , onda se hipoteza o pouzdanosti razlika između uzoraka odbacuje, ako t exp. > t cr. , onda je prihvaćeno. Drugim riječima, uzorci se međusobno značajno razlikuju ako je Studentov koeficijent izračunat po formuli veći od tabelarne vrijednosti za odgovarajući nivo značajnosti.
U problemu koji smo ranije razmatrali, izračun prosječnih vrijednosti i varijansi daje sljedeće vrijednosti: x cf. = 38,5; σ x 2 = 28,40; at cf. = 36,2; σ y 2 = 31,72.
Vidi se da je prosječna vrijednost anksioznosti u grupi djevojčica veća nego u grupi dječaka. Međutim, ove razlike su toliko male da je malo vjerovatno da će biti statistički značajne. Rascjep vrijednosti kod dječaka je, naprotiv, nešto veći nego kod djevojčica, ali su i razlike između varijansi male.

Zaključak
t exp. = 1,14< t cr. = 2,05 (β 1 = 0,95). Razlike između dva upoređena uzorka nisu statistički značajne. Ovaj zaključak je prilično konzistentan sa onim dobivenim korištenjem kriterija Rosenbaum i Mann-Whitney.
Drugi način da se utvrde razlike između dva uzorka koristeći Studentov t-test je izračunavanje intervala pouzdanosti standardnih devijacija. Interval pouzdanosti je srednja kvadratna (standardna) devijacija podijeljena s kvadratnim korijenom veličine uzorka i pomnožena sa standardnom vrijednošću Studentovog koeficijenta za n– 1 stepen slobode (odnosno, i ).
Bilješka
Vrijednost = mx naziva se srednja kvadratna greška (vidi Odjeljak 5). Stoga je interval povjerenja standardna greška pomnožena Studentovim koeficijentom za datu veličinu uzorka, gdje je broj stupnjeva slobode ν = n- 1 i za dati nivo značaj.
Dva uzorka koja su neovisna jedan od drugog smatraju se značajno različitim ako se intervali povjerenja za ove uzorke ne preklapaju jedan s drugim. U našem slučaju imamo 38,5 ± 2,84 za prvi uzorak i 36,2 ± 3,38 za drugi.
Dakle, slučajne varijacije x i leže u rasponu 35,66 ¸ 41,34, i varijacije y i- u rasponu 32,82 ¸ 39,58. Na osnovu ovoga može se konstatovati da su razlike između uzoraka x I y statistički nepouzdan (opsezi varijacija se međusobno preklapaju). U ovom slučaju treba imati na umu da širina zone preklapanja u ovom slučaju nije bitna (važna je samo sama činjenica preklapanja intervala povjerenja).
Studentova metoda za međuzavisne uzorke (na primjer, za upoređivanje rezultata dobijenih ponovljenim testiranjem na istom uzorku ispitanika) se koristi prilično rijetko, jer postoje druge, informativnije statističke tehnike za ove svrhe (vidi Odjeljak 10). Međutim, u tu svrhu, kao prvu aproksimaciju, možete koristiti Studentovu formulu sljedećeg oblika:
 (7.3)
(7.3)
Dobijeni rezultat se poredi sa tabelarnom vrednošću za n– 1 stepen slobode, gde n– broj parova vrijednosti x I y. Rezultati poređenja se tumače na potpuno isti način kao u slučaju izračunavanja razlika između dva nezavisna uzorka.
Fišerov kriterijum
Fišerov kriterijum ( F) se zasniva na istom principu kao i Studentov t-test, odnosno uključuje izračunavanje srednjih vrijednosti i varijansi u upoređenim uzorcima. Najčešće se koristi kada se međusobno uspoređuju uzorci nejednake veličine (različite veličine). Fisherov test je nešto stroži od Studentovog testa, pa je poželjniji u slučajevima kada postoje sumnje u pouzdanost razlika (na primjer, ako su, prema Studentovom testu, razlike značajne na nuli, a nisu značajne pri prvoj značajnosti nivo).
Fisherova formula izgleda ovako:
 (7.4)
(7.4)
gdje i  (7.5, 7.6)
(7.5, 7.6)
U našem problemu d2= 5,29; σz 2 = 29,94.
Zamijenite vrijednosti u formuli: ![]()
U tabeli. XI aplikacijama nalazimo da je za nivo značajnosti β 1 = 0,95 i ν = n x + n y - 2 = 28 kritična vrijednost je 4,20.
Zaključak
F = 1,32 < F cr.= 4,20. Razlike između uzoraka nisu statistički značajne.
Bilješka
Kada se koristi Fišerov test, moraju biti ispunjeni isti uslovi kao i za Studentov test (videti pododeljak 7.4). Ipak, dozvoljena je razlika u broju uzoraka za više od dva puta.
Dakle, rješavajući isti problem sa četiri različite metode korištenjem dva neparametarska i dva parametarska kriterija, došli smo do nedvosmislenog zaključka da su razlike između grupe djevojčica i grupe dječaka u pogledu nivoa reaktivne anksioznosti nepouzdane (tj. , su unutar slučajne varijacije). Međutim, mogu postojati slučajevi kada nije moguće donijeti nedvosmislen zaključak: neki kriteriji daju pouzdane, drugi - nepouzdane razlike. U tim slučajevima prioritet se daje parametarskim kriterijima (u zavisnosti od dovoljnosti veličine uzorka i normalne distribucije vrijednosti koje se proučavaju).
7. 6. Kriterij j* - Fisherova kutna transformacija
Kriterij j*Fisher je dizajniran da uporedi dva uzorka prema učestalosti pojavljivanja efekta od interesa za istraživača. Procjenjuje se značajnost razlika između procenta dva uzorka u kojima je registrovan efekat interesa. Dozvoljeno je i poređenje procenata unutar istog uzorka.
esencija kutna transformacija Fisher pretvara procente u centralne uglove, koji se mjere u radijanima. Veći procenat će odgovarati većem uglu j, a manji udio - manji ugao, ali je odnos ovdje nelinearan:
![]()
Gdje R– procenat, izražen u ulomcima jedinice.
Sa povećanjem neslaganja između uglova j 1 i j 2 i povećanjem broja uzoraka, vrednost kriterijuma raste.
Fisherov kriterij se izračunava po sljedećoj formuli:
| |
gdje je j 1 ugao koji odgovara većem procentu; j 2 - ugao koji odgovara manjem procentu; n 1 i n 2 - volumen prvog i drugog uzorka.
Vrijednost izračunata formulom upoređuje se sa standardnom vrijednošću (j* st = 1,64 za b 1 = 0,95 i j* st = 2,31 za b 2 = 0,99. Razlike između dva uzorka smatraju se statistički značajnim ako je j*> j* st za dati nivo značaja.
Primjer
Zanima nas da li se dvije grupe učenika međusobno razlikuju po uspješnosti rješavanja prilično složenog zadatka. U prvoj grupi od 20 ljudi, 12 učenika se snašlo, u drugoj - 10 osoba od 25.
Rješenje
1. Unesite notaciju: n 1 = 20, n 2 = 25.
2. Izračunajte procente R 1 i R 2: R 1 = 12 / 20 = 0,6 (60%), R 2 = 10 / 25 = 0,4 (40%).
3. U tabeli. XII Primjenama nalazimo vrijednosti φ koje odgovaraju procentima: j 1 = 1,772, j 2 = 1,369.
| |
Odavde:
Zaključak
Razlike između grupa nisu statistički značajne jer j*< j* ст для 1-го и тем более для 2-го уровня значимости.
7.7. Koristeći Pearsonov χ2 test i Kolmogorovljev λ test
Naravno, pri izračunavanju funkcije kumulativne distribucije treba koristiti pomenuti odnos između binomne i beta distribucije. Ova metoda je svakako bolja od direktnog zbrajanja kada je n > 10.
U klasičnim udžbenicima iz statistike, za dobivanje vrijednosti binomne distribucije, često se preporučuje korištenje formula zasnovanih na graničnim teoremama (kao što je Moivre-Laplaceova formula). Treba napomenuti da sa čisto računske tačke gledišta vrijednost ovih teorema je blizu nule, pogotovo sada, kada je moćan kompjuter na skoro svakom stolu. Glavni nedostatak gornjih aproksimacija je njihova potpuno nedovoljna tačnost za vrijednosti n tipične za većinu aplikacija. Ništa manji nedostatak je nepostojanje bilo kakvih jasnih preporuka o primjenjivosti jedne ili druge aproksimacije (u standardnim tekstovima date su samo asimptotske formulacije, nisu praćene procjenama tačnosti i stoga su od male koristi). Rekao bih da obje formule vrijede samo za n< 200 и для совсем грубых, ориентировочных расчетов, причем делаемых “вручную” с помощью статистических таблиц. А вот связь между биномиальным распределением и бета-распределением позволяет вычислять биномиальное распределение достаточно экономно.
Ovdje ne razmatram problem pronalaženja kvantila: za diskretne distribucije on je trivijalan, au onim problemima gdje se takve distribucije javljaju, po pravilu nije relevantan. Ako su kvantili i dalje potrebni, preporučujem da se problem preformuliše na takav način da radi sa p-vrijednostima (uočene značajnosti). Evo primjera: kada se implementiraju neki algoritami nabrajanja, u svakom koraku potrebno je provjeriti statistička hipoteza o binomnoj slučajnoj varijabli. Prema klasičnom pristupu, na svakom koraku potrebno je izračunati statistiku kriterija i uporediti njegovu vrijednost sa granicom kritičnog skupa. Kako je, međutim, algoritam enumerativan, potrebno je svaki put iznova odrediti granicu kritičnog skupa (na kraju krajeva, veličina uzorka se mijenja iz koraka u korak), što neproduktivno povećava vremenske troškove. Moderan pristup preporučuje izračunavanje uočene važnosti i poređenje sa nivo samopouzdanja, štedeći na potrazi za kvantilima.
Stoga, sljedeći kodovi ne izračunavaju inverznu funkciju, umjesto toga, data je funkcija rev_binomialDF, koja izračunava vjerovatnoću p uspjeha u jednom pokušaju s obzirom na broj n pokušaja, broj m uspjeha u njima i vrijednost y vjerovatnoće da ćete postići ove m uspjeha. Ovo koristi gore spomenuti odnos između binomne i beta distribucije.
Zapravo, ova funkcija vam omogućava da dobijete granice intervala povjerenja. Zaista, pretpostavimo da dobijemo m uspjeha u n binomnih pokušaja. Kao što je poznato, lijeva granica dvostranog intervala povjerenja za parametar p sa nivoom povjerenja je 0 ako je m = 0, a za je rješenje jednadžbe  . Slično, desna granica je 1 ako je m = n, a za je rješenje jednadžbe
. Slično, desna granica je 1 ako je m = n, a za je rješenje jednadžbe  . To implicira da da bismo pronašli lijevu granicu, moramo riješiti jednačinu
. To implicira da da bismo pronašli lijevu granicu, moramo riješiti jednačinu  , a za traženje pravog - jednačina
, a za traženje pravog - jednačina  . Oni su riješeni u funkcijama binom_leftCI i binom_rightCI, koje vraćaju gornju i donju granicu dvostranog intervala povjerenja, respektivno.
. Oni su riješeni u funkcijama binom_leftCI i binom_rightCI, koje vraćaju gornju i donju granicu dvostranog intervala povjerenja, respektivno.
Želim napomenuti da ako nije potrebna apsolutno nevjerojatna tačnost, onda za dovoljno veliko n možete koristiti sljedeću aproksimaciju [B.L. van der Waerden, Matematička statistika. M: IL, 1960, Ch. 2, sek. 7]:  , gdje je g kvantil normalne distribucije. Vrijednost ove aproksimacije je u tome što postoje vrlo jednostavne aproksimacije koje vam omogućavaju da izračunate kvantile normalne distribucije (pogledajte tekst o izračunavanju normalne distribucije i odgovarajući dio ove reference). U mojoj praksi (uglavnom za n > 100) ova aproksimacija je dala oko 3-4 cifre, što je po pravilu sasvim dovoljno.
, gdje je g kvantil normalne distribucije. Vrijednost ove aproksimacije je u tome što postoje vrlo jednostavne aproksimacije koje vam omogućavaju da izračunate kvantile normalne distribucije (pogledajte tekst o izračunavanju normalne distribucije i odgovarajući dio ove reference). U mojoj praksi (uglavnom za n > 100) ova aproksimacija je dala oko 3-4 cifre, što je po pravilu sasvim dovoljno.
Izračuni sa sljedećim kodovima zahtijevaju datoteke betaDF.h, betaDF.cpp (pogledajte odjeljak o beta distribuciji), kao i logGamma.h, logGamma.cpp (pogledajte dodatak A). Također možete vidjeti primjer korištenja funkcija.
binomialDF.h fajl
| #ifndef __BINOMIAL_H__ #include "betaDF.h" dvostruki binomni DF (dvostruki pokušaji, dvostruki uspjesi, dvostruki p); /* * Neka postoje "pokusi" nezavisnih zapažanja * sa vjerovatnoćom "p" uspjeha u svakom. * Izračunajte vjerovatnoću B(uspjesi|pokušaji,p) da je broj * uspjeha između 0 i "uspjeha" (uključivo). */ double rev_binomialDF(dvostruki pokušaji, dvostruki uspjesi, dvostruki y); /* * Neka je vjerovatnoća y od najmanje m uspjeha * poznata u ispitivanjima Bernoullijeve šeme. Funkcija pronalazi vjerovatnoću p * uspjeha u jednom pokušaju. * * U proračunima se koristi sljedeća relacija * * 1 - p = rev_Beta(pokušaji-uspjesi| uspjesi+1, y). */ double binom_leftCI(dvostruki pokušaji, dvostruki uspjesi, dvostruki nivo); /* Neka postoje "pokusi" nezavisnih zapažanja * sa vjerovatnoćom "p" uspjeha u svakom * i broj uspjeha je "uspjesi". * Lijeva granica dvostranog intervala povjerenja * izračunava se sa nivoom značaja. */ double binom_rightCI(dvostruki n, dvostruki uspjesi, dvostruki nivo); /* Neka postoje "pokusi" nezavisnih zapažanja * sa vjerovatnoćom "p" uspjeha u svakom * i broj uspjeha je "uspjesi". * Desna granica dvostranog intervala pouzdanosti * izračunava se sa nivoom značaja. */ #endif /* Završava #ifndef __BINOMIAL_H__ */ |
binomialDF.cpp fajl
| /************************************************** **** **********/ /* Binomna distribucija */ /****************************** **** **************************/ #include |
Pozdrav svim čitaocima!
Statistička analiza se, kao što znate, bavi prikupljanjem i obradom stvarnih podataka. To je korisno, a često i isplativo, jer. pravi zaključci vam omogućavaju da izbjegnete greške i gubitke u budućnosti, a ponekad i ispravno pogodite ovu budućnost. Prikupljeni podaci odražavaju stanje neke uočene pojave. Podaci su često (ali ne uvijek) numerički i njima se može manipulirati raznim matematičkim manipulacijama kako bi se izvukle dodatne informacije.
Međutim, ne mjere se svi fenomeni u kvantitativnoj skali kao što je 1, 2, 3... 100500... Ne može uvijek pojava poprimiti beskonačan ili veliki broj različitih stanja. Na primjer, spol osobe može biti ili M ili F. Strijelac ili pogađa metu ili promašuje. Možete glasati ili "za" ili "protiv" itd. i tako dalje. Drugim riječima, takvi podaci odražavaju stanje alternativnog atributa - ili "da" (događaj se dogodio) ili "ne" (događaj se nije dogodio). Nadolazeći događaj (pozitivan ishod) naziva se i "uspjeh". Takve pojave takođe mogu biti masovne i nasumične. Stoga se mogu izmjeriti i izvući statistički valjani zaključci.
Eksperimenti sa takvim podacima se nazivaju Bernoullijeva šema, u čast poznatog švajcarskog matematičara koji je to ustanovio kada u velikom broju ispitivanja, omjer pozitivnih ishoda i ukupnog broja ispitivanja teži vjerovatnoći da se ovaj događaj dogodi.
Alternativna varijabla funkcije
Da bi se u analizi koristio matematički aparat, rezultate takvih opažanja treba zapisati u numeričkom obliku. Da bi se to postiglo, pozitivnom ishodu se dodeljuje broj 1, negativnom - 0. Drugim rečima, radi se o promenljivoj koja može imati samo dve vrednosti: 0 ili 1.
Kakva korist se može izvući iz ovoga? Zapravo, ništa manje nego iz običnih podataka. Dakle, lako je izbrojati broj pozitivnih ishoda – dovoljno je sabrati sve vrijednosti, tj. sve 1 (uspjeh). Možete ići dalje, ali za ovo morate uvesti nekoliko oznaka.
Prva stvar koju treba primijetiti je da pozitivni ishodi (koji su jednaki 1) imaju izvjesnu vjerovatnoću da će se dogoditi. Na primjer, dobijanje glave pri bacanju novčića je ½ ili 0,5. Ova vjerovatnoća se tradicionalno označava latinično pismo str. Stoga je vjerovatnoća da se dogodi alternativni događaj 1-p, što je takođe označeno sa q, to je q = 1 – str. Ove oznake se mogu vizualno sistematizirati u obliku promjenjive distribucijske ploče X.
Sada imamo listu mogućih vrijednosti i njihove vjerovatnoće. Možete početi izračunavati tako divne karakteristike slučajne varijable kao što je očekivanu vrijednost I disperzija. Da vas podsjetim da se matematičko očekivanje izračunava kao zbir proizvoda svih mogućih vrijednosti i njihovih odgovarajućih vjerovatnoća:
![]()
Izračunajmo očekivanu vrijednost koristeći notaciju u gornjim tabelama.
Ispada da je matematičko očekivanje alternativnog znaka jednako vjerovatnoći ovog događaja - str.
Hajde sada da definišemo šta je varijansa alternativne karakteristike. Dozvolite mi također da vas podsjetim da je varijansa srednji kvadrat odstupanja od matematičkog očekivanja. Opća formula(za diskretne podatke) ima oblik:
Otuda varijansa alternativne karakteristike:

Lako je vidjeti da ova disperzija ima maksimum od 0,25 (at p=0,5).
Standardna devijacija - korijen varijanse:
Maksimalna vrijednost ne prelazi 0,5.
Kao što možete vidjeti, i matematičko očekivanje i varijansa alternativnog znaka imaju vrlo kompaktan oblik.
Binomna distribucija slučajne varijable
Sada razmotrite situaciju iz drugog ugla. Zaista, koga briga što je prosječan gubitak glava pri jednom bacanju 0,5? To je čak nemoguće i zamisliti. Zanimljivije je postaviti pitanje o broju glava koje dolaze za dati broj bacanja.
Drugim riječima, istraživača često zanima vjerovatnoća da će se desiti određeni broj uspješnih događaja. To može biti broj neispravnih proizvoda u testiranoj seriji (1 - neispravan, 0 - dobar) ili broj oporavljenih (1 - zdrav, 0 - bolestan) itd. Broj takvih "uspjeha" bit će jednak zbroju svih vrijednosti varijable X, tj. broj pojedinačnih ishoda.
Slučajna vrijednost B naziva se binom i uzima vrijednosti od 0 do n(u B= 0 - svi dijelovi su dobri, sa B = n- svi dijelovi su neispravni). Pretpostavlja se da su sve vrijednosti x nezavisni jedno od drugog. Razmotrimo glavne karakteristike binomske varijable, odnosno ustanovićemo njeno matematičko očekivanje, varijansu i distribuciju.
Očekivanje binomske varijable je vrlo lako dobiti. Podsjetimo da postoji zbir matematičkih očekivanja svake dodane vrijednosti i da je isti za sve, dakle:
Na primjer, očekivanje broja glava na 100 bacanja je 100 × 0,5 = 50.
Sada izvodimo formulu za varijansu binomske varijable. je zbir varijansi. Odavde
Standardna devijacija, respektivno
Za 100 bacanja novčića, standardna devijacija je
I na kraju, razmotrite distribuciju binomna vrijednost, tj. vjerovatnoća da je slučajna varijabla Bće uzeti razna značenja k, Gdje 0≤k≤n. Za novčić, ovaj problem bi mogao zvučati ovako: kolika je vjerovatnoća da dobijete 40 grla u 100 bacanja?
Da bismo razumjeli način izračunavanja, zamislimo da se novčić baci samo 4 puta. Svaka strana može ispasti svaki put. Pitamo se: kolika je vjerovatnoća da dobijemo 2 glave od 4 bacanja. Svako bacanje je nezavisno jedno od drugog. To znači da će vjerovatnoća dobivanja bilo koje kombinacije biti jednaka proizvodu vjerovatnoće datog ishoda za svako pojedinačno bacanje. Neka su O glave i P repovi. Tada, na primjer, jedna od kombinacija koja nam odgovara može izgledati kao OOPP, odnosno:

Vjerovatnoća takve kombinacije jednaka je umnošku dvije vjerovatnoće izbijanja i još dvije vjerovatnoće neuspjeha (obrnuti događaj izračunat kao 1-p), tj. 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Ovo je vjerovatnoća jedne od kombinacija koja nam odgovara. Ali pitanje je bilo o ukupnom broju orlova, a ne o nekom posebnom redu. Zatim trebate sabrati vjerovatnoće svih kombinacija u kojima se nalaze tačno 2 orla. Jasno je da su svi isti (proizvod se ne mijenja od promjene mjesta faktora). Stoga morate izračunati njihov broj, a zatim pomnožiti s vjerovatnoćom bilo koje takve kombinacije. Izbrojimo sve kombinacije od 4 bacanja 2 orla: RROO, RORO, ROOR, ORRO, OROR, OORR. Samo 6 opcija.

Dakle, željena vjerovatnoća da dobijete 2 glave nakon 4 bacanja je 6×0,0625=0,375.
Međutim, brojanje na ovaj način je zamorno. Već za 10 novčića bit će vrlo teško dobiti ukupan broj opcija grubom silom. Stoga su pametni ljudi davno izmislili formulu uz pomoć koje izračunavaju broj različitih kombinacija n elementi po k, Gdje n je ukupan broj elemenata, k je broj elemenata čije su opcije rasporeda izračunate. Kombinovana formula od n elementi po k je:
![]()
Slične stvari se dešavaju u sekciji kombinatorike. Saljem tamo sve koji zele da unaprede svoje znanje. Otuda, inače, naziv binomne distribucije (gornja formula je koeficijent u ekspanziji Njutnovog binoma).
Formula za određivanje vjerovatnoće može se lako generalizirati na bilo koji broj n I k. Kao rezultat, formula binomne distribucije ima sljedeći oblik.
Drugim riječima: pomnožite broj odgovarajućih kombinacija vjerovatnoćom jedne od njih.
Za praktična upotreba dovoljno je samo znati formulu binomne distribucije. A možda čak i ne znate - u nastavku je kako odrediti vjerovatnoću koristeći Excel. Ali bolje je znati.
Koristimo ovu formulu da izračunamo vjerovatnoću da dobijemo 40 glava u 100 bacanja:
Ili samo 1,08%. Poređenja radi, vjerovatnoća matematičkog očekivanja ovog eksperimenta, odnosno 50 grla je 7,96%. Maksimalna vjerovatnoća binomske vrijednosti pripada vrijednosti koja odgovara matematičkom očekivanju.
Izračunavanje vjerovatnoće binomne distribucije u Excelu
Ako koristite samo papir i kalkulator, onda izračunajte pomoću formule binomna distribucija, uprkos odsustvu integrala, prilično su teške. Na primjer, vrijednost od 100! - ima više od 150 karaktera. Ovo je nemoguće izračunati ručno. Ranije, pa čak i sada, za izračunavanje takvih količina korištene su približne formule. Trenutno je preporučljivo koristiti poseban softver, kao što je MS Excel. Dakle, svaki korisnik (čak i humanista po obrazovanju) može lako izračunati vjerovatnoću vrijednosti binomno raspoređene slučajne varijable.
Za konsolidaciju gradiva koristićemo za sada Excel kao običan kalkulator, tj. Napravimo korak po korak izračunavanje koristeći formulu binomne distribucije. Izračunajmo, na primjer, vjerovatnoću da dobijemo 50 grla. Ispod je slika sa koracima proračuna i konačnim rezultatom.

Kao što vidite, međurezultati su takve skale da ne stanu u ćeliju, iako se posvuda koriste jednostavne funkcije tipa: FAKTOR (faktorski proračun), POWER (podizanje broja na stepen), kao i kao operatori množenja i dijeljenja. Štaviše, ovaj proračun je prilično glomazan, u svakom slučaju nije kompaktan, jer uključene mnoge ćelije. I da, teško je to shvatiti.
Generalno, Excel pruža gotovu funkciju za izračunavanje vjerovatnoća binomne distribucije. Funkcija se zove BINOM.DIST.

Broj uspjeha je broj uspješnih pokušaja. Imamo ih 50.
Broj pokušaja- broj bacanja: 100 puta.
Vjerovatnoća uspjeha– vjerovatnoća dobijanja glave pri jednom bacanju je 0,5.
Integral- naznačeno je ili 1 ili 0. Ako je 0, tada se izračunava vjerovatnoća P(B=k); ako je 1, onda se izračunava funkcija binomne distribucije, tj. zbir svih vjerovatnoća iz B=0 prije B=k inkluzivno.
Pritisnemo OK i dobijemo isti rezultat kao gore, samo što je sve izračunato po jednoj funkciji.

Vrlo udobno. Eksperimenta radi, umjesto posljednjeg parametra 0 stavljamo 1. Dobijamo 0,5398. To znači da je u 100 bacanja novčića vjerovatnoća da dobijete glave između 0 i 50 skoro 54%. I u početku se činilo da bi trebalo da bude 50%. Općenito, proračuni se rade lako i brzo.
Pravi analitičar mora razumjeti kako se funkcija ponaša (kakva je njena distribucija), pa hajde da izračunamo vjerovatnoće za sve vrijednosti od 0 do 100. Odnosno, zapitajmo se: kolika je vjerovatnoća da nijedan orao neće pasti, da će 1 orao pasti, 2, 3, 50, 90 ili 100. Izračun je prikazan na sljedećoj samopokretnoj slici. Plava linija je sama binomna distribucija, crvena tačka je vjerovatnoća za određeni broj uspjeha k.

Moglo bi se zapitati, nije li binomna distribucija slična... Da, vrlo slična. Čak je i De Moivre (1733.) rekao da se sa velikim uzorcima približava binomska distribucija (ne znam kako se tada zvala), ali ga niko nije slušao. Tek su Gaus, a potom i Laplace, 60-70 godina kasnije, ponovo otkrili i pažljivo proučili zakon normalne raspodjele. Gornji grafikon jasno pokazuje da maksimalna vjerovatnoća pada na matematičko očekivanje, a kako odstupa od njega, naglo opada. Baš kao normalan zakon.
Binomna distribucija je od velike praktične važnosti, javlja se prilično često. Korišćenjem Excel proračuni izvode brzo i lako. Stoga ga slobodno koristite.
Na ovome predlažem da se pozdravimo do sljedećeg sastanka. Sve najbolje, budite zdravi!




