". U prvom dijelu su navedene odredbe koje su minimalno neophodne za razumijevanje kemometrije, a drugi dio sadrži činjenice koje trebate znati za dublje razumijevanje metoda multivarijantne analize. Prezentacija je ilustrovana primjerima napravljenim u Excel radnoj svesci Matrix.xls koji prati ovaj dokument.

Veze na primjere se postavljaju u tekst kao Excel objekti. Ovi primjeri su apstraktne prirode, ni na koji način nisu vezani za zadatke. analitička hemija. Pravi primjeri o upotrebi matrične algebre u hemometriji govori se u drugim tekstovima posvećenim različitim kemometrijskim aplikacijama.

Većina mjerenja u analitičkoj hemiji nisu direktna, ali indirektno. To znači da se u eksperimentu, umjesto vrijednosti željenog analita C (koncentracija), dobije druga vrijednost x(signal) povezan sa, ali nije jednak C, tj. x(C) ≠ C. Po pravilu, vrsta zavisnosti x(C) nije poznato, ali na sreću u analitičkoj hemiji većina mjerenja je proporcionalna. To znači da kao koncentracija C in a puta, signal X će se povećati za isti iznos, tj. x(a C) = sjekira(C). Osim toga, signali su i aditivni, tako da će signal iz uzorka koji sadrži dvije supstance sa koncentracijama C 1 i C 2 biti jednak zbiru signala svake komponente, tj. x(C1 + C2) = x(C1)+ x(C2). Proporcionalnost i aditivnost zajedno daju linearnost. Može se navesti mnogo primjera da se ilustruje princip linearnosti, ali dovoljno je spomenuti dva najupečatljivija primjera - hromatografiju i spektroskopiju. Druga karakteristika inherentna eksperimentu u analitičkoj hemiji je višekanalni. Moderna analitička oprema istovremeno mjeri signale za mnoge kanale. Na primjer, intenzitet propuštanja svjetlosti se mjeri za nekoliko talasnih dužina odjednom, tj. domet. Stoga, u eksperimentu imamo posla sa različitim signalima x 1 , x 2 ,...., x n karakterizira skup koncentracija C 1 ,C 2 , ..., C m supstanci prisutnih u sistemu koji se proučava.

Rice. 1 Spectra

Dakle, analitički eksperiment karakteriziraju linearnost i višedimenzionalnost. Stoga je zgodno eksperimentalne podatke posmatrati kao vektore i matrice i manipulirati njima pomoću aparata matrične algebre. Plodnost ovog pristupa ilustruje primjer prikazan u , koji prikazuje tri spektra snimljena za 200 valnih dužina od 4000 do 4796 cm–1. Prvi ( x 1) i drugi ( x 2) spektri su dobijeni za standardne uzorke u kojima su poznate koncentracije dvije supstance A i B: u prvom uzorku [A] = 0,5, [B] = 0,1, au drugom uzorku [A] = 0,2, [ B] = 0,6. Šta reći o novom, nepoznatom uzorku, čiji je spektar naznačen x 3 ?

Razmotrimo tri eksperimentalna spektra x 1 , x 2 i x 3 kao tri vektora dimenzije 200. Koristeći linearnu algebru, to se lako može pokazati x 3 = 0.1 x 1 +0.3 x 2 , tako da treći uzorak očigledno sadrži samo supstance A i B u koncentracijama [A] = 0,5×0,1 + 0,2×0,3 = 0,11 i [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Osnovne informacije

1.1 Matrice

Matrix nazvana, na primjer, pravokutna tablica brojeva

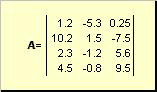
Rice. 2 Matrix

Matrice su označene velikim podebljanim slovima ( A), a njihovi elementi - odgovarajućim malim slovima sa indeksima, tj. a ij . Prvi indeks numerira redove, a drugi broj stupaca. U kemometriji je uobičajeno da se maksimalna vrijednost indeksa označi istim slovom kao i sam indeks, ali velikim slovima. Dakle, matrica A može se napisati i kao ( a ij , i = 1,..., I; j = 1,..., J). Za primjer matrice I = 4, J= 3 i a 23 = −7.5.

Par brojeva I i J naziva se dimenzija matrice i označava se kao I× J. Primjer matrice u kemometriji je skup spektra dobivenih za I uzorci na J talasne dužine.

1.2. Najjednostavnije operacije sa matricama

Matrice mogu pomnožiti brojevima. U ovom slučaju, svaki element se množi ovim brojem. Na primjer -

Rice. 3 Množenje matrice brojem

Dvije matrice iste dimenzije mogu biti elementarne fold i oduzimati. Na primjer,

Rice. 4 Sabiranje matrice

Kao rezultat množenja brojem i sabiranja, dobiva se matrica iste dimenzije.

Nulta matrica je matrica koja se sastoji od nula. Određeno je O. Očigledno je da A+O = A, A−A = O i 0 A = O.

Matrica može transponovati. Tokom ove operacije, matrica se okreće, tj. redovi i kolone se zamjenjuju. Transpozicija je označena crticom, A" ili indeks A t . Dakle, ako A = {a ij , i = 1,..., I; j = 1,...,J), onda A t = ( a ji , j = 1,...,J; i = 1,..., I). Na primjer

Rice. 5 Matrična transpozicija

Očigledno je da ( A t) t = A, (A+B) t = A t + B t .

1.3. Množenje matrice

Matrice mogu umnožiti, ali samo ako imaju odgovarajuće dimenzije. Zašto je to tako, biće jasno iz definicije. Matrični proizvod A, dimenzija I× K, i matrice B, dimenzija K× J, naziva se matrica C, dimenzija I× J, čiji su elementi brojevi

Dakle, za proizvod AB potrebno je da broj kolona u lijevoj matrici A bio jednak broju redova u desnoj matrici B. Primjer matričnog proizvoda -

Slika 6 Proizvod matrica

Pravilo množenja matrice može se formulirati na sljedeći način. Za pronalaženje elementa matrice C stoji na raskrsnici i-ti red i j-ta kolona ( c ij) mora se pomnožiti element po element i-ti red prve matrice A on j-ti stupac druge matrice B i zbrojite sve rezultate. Dakle, u prikazanom primjeru, element iz trećeg reda i drugog stupca dobijen je kao zbir proizvoda trećeg reda po elementima A i druga kolona B

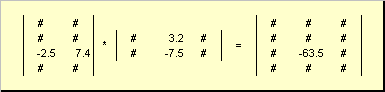
Slika 7 Element proizvoda matrica

Proizvod matrica zavisi od redosleda, tj. AB ≠ BA, barem iz dimenzionalnih razloga. Kaže se da je nekomutativno. Međutim, proizvod matrica je asocijativan. To znači da ABC = (AB)C = A(BC). Štaviše, ona je i distributivna, tj. A(B+C) = AB+AC. Očigledno je da AO = O.

1.4. Kvadratne matrice

Ako je broj stupaca matrice jednak broju njenih redova ( I = J=N), tada se takva matrica naziva kvadratna. U ovom dijelu ćemo razmotriti samo takve matrice. Među ovim matricama mogu se izdvojiti matrice sa posebnim svojstvima.

Samica matrica (označeno I i ponekad E) je matrica u kojoj su svi elementi jednaki nuli, osim dijagonalnih, koji su jednaki 1, tj.

Očigledno AI = IA = A.

Matrica se zove dijagonala, ako su svi njegovi elementi, osim dijagonalnih ( a ii) jednaki su nuli. Na primjer

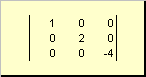
Rice. 8 Dijagonalna matrica

Matrix A zove vrh trouglasti, ako su svi njegovi elementi koji leže ispod dijagonale jednaki nuli, tj. a ij= 0, at i>j. Na primjer

Rice. 9 Gornja trokutasta matrica

Donja trokutasta matrica definirana je na sličan način.

Matrix A pozvao simetrično, ako A t = A. Drugim riječima a ij = a ji. Na primjer

Rice. 10 Simetrična matrica

Matrix A pozvao ortogonalno, ako

A t A = aa t = I.

Matrica se zove normalno ako

1.5. Trag i determinanta

Praćenje kvadratna matrica A(označeno Tr( A) ili Sp( A)) je zbir njegovih dijagonalnih elemenata,

Na primjer,

Rice. 11 Trag matrice

Očigledno je da

Sp(α A) = α Sp( A) i

Sp( A+B) = Sp( A)+ Sp( B).

To se može pokazati

Sp( A) = Sp( A t), Sp( I) = N,

a takođe i to

Sp( AB) = Sp( BA).

Još jedna važna karakteristika kvadratne matrice je njena odrednica(označeno sa det( A)). Definicija determinante u opšti slučaj prilično komplicirano, pa ćemo početi s najjednostavnijom opcijom - matricom A dimenzija (2×2). Onda

Za (3×3) matricu, determinanta će biti jednaka

U slučaju matrice ( N× N) determinanta se izračunava kao zbir 1 2 3 ... N= N! pojmova, od kojih je svaki jednak

Indeksi k 1 , k 2 ,..., kN definirani su kao sve moguće uređene permutacije r brojevi u skupu (1, 2, ... , N). Izračunavanje determinante matrice je složen postupak koji se u praksi izvodi pomoću posebnih programa. Na primjer,

Rice. 12 Matrična determinanta

Napominjemo samo očigledna svojstva:

det( I) = 1, det( A) = det( A t),

det( AB) = det( A)det( B).

1.6. Vektori

Ako matrica ima samo jedan stupac ( J= 1), onda se takav objekat naziva vektor. Tačnije, vektor kolone. Na primjer

Na primjer, mogu se uzeti u obzir i matrice koje se sastoje od jednog reda

Ovaj objekt je također vektor, ali vektor reda. Prilikom analize podataka važno je razumjeti s kojim vektorima imamo posla – stupcima ili redovima. Dakle, spektar uzet za jedan uzorak može se smatrati vektorom reda. Tada skup spektralnih intenziteta na nekoj talasnoj dužini za sve uzorke treba tretirati kao vektor kolone.

Dimenzija vektora je broj njegovih elemenata.

Jasno je da se bilo koji vektor kolone može transformisati u vektor reda transpozicijom, tj.

U onim slučajevima kada oblik vektora nije posebno određen, već se jednostavno kaže vektor, onda oni označavaju vektor stupac. I mi ćemo se pridržavati ovog pravila. Vektor se označava malim direktnim podebljanim slovom. Nulti vektor je vektor čiji su svi elementi jednaki nuli. To je označeno 0 .

1.7. Najjednostavnije operacije sa vektorima

Vektori se mogu sabirati i množiti brojevima na isti način kao i matrice. Na primjer,

Rice. 13 Operacije s vektorima

Dva vektora x i y pozvao kolinearno, ako postoji broj α takav da

1.8. Proizvodi vektora

Dva vektora iste dimenzije N može se umnožiti. Neka postoje dva vektora x = (x 1 , x 2 ,...,x N) t i y = (y 1 , y 2 ,...,y N) t . Vođeni pravilom množenja "red po stupac", od njih možemo napraviti dva proizvoda: x t y i xy t . Prvi rad

pozvao skalar ili interni. Njegov rezultat je broj. Takođe koristi notaciju ( x,y)= x t y. Na primjer,

Rice. 14 Unutrašnji (skalarni) proizvod

Drugi rad

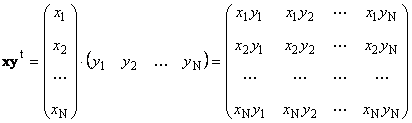
pozvao vanjski. Njegov rezultat je matrica dimenzija ( N× N). Na primjer,

Rice. 15 Spoljašnji proizvod

Pozivaju se vektori čiji je skalarni proizvod jednak nuli ortogonalno.

1.9. Vektorska norma

Skalarni proizvod vektora sa samim sobom naziva se skalarni kvadrat. Ova vrijednost

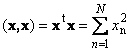
definira kvadrat dužina vektor x. Za označavanje dužine (takođe se naziva norma vektor) koristi se notacija

Na primjer,

Rice. 16 Vektorska norma

Vektor jedinične dužine (|| x|| = 1) naziva se normalizovano. Nenulti vektor ( x ≠ 0 ) može se normalizirati dijeljenjem dužine, tj. x = ||x|| (x/||x||) = ||x|| e. Evo e = x/||x|| je normalizovan vektor.

Vektori se nazivaju ortonormalni ako su svi normalizirani i po paru ortogonalni.

1.10. Ugao između vektora

Skalarni proizvod definira i ugaoφ između dva vektora x i y

Ako su vektori ortogonalni, onda je cosφ = 0 i φ = π/2, a ako su kolinearni, onda je cosφ = 1 i φ = 0.

1.11. Vektorska reprezentacija matrice

Svaka matrica A veličina I× J može se predstaviti kao skup vektora

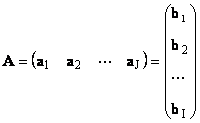
Ovdje svaki vektor a j je j-ta kolona i vektor reda b i je i-ti red matrice A

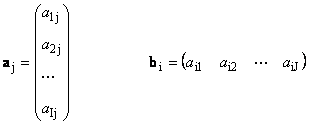
1.12. Linearno zavisni vektori

Vektori iste dimenzije ( N) može se dodati i pomnožiti brojem, baš kao matrice. Rezultat je vektor iste dimenzije. Neka postoji nekoliko vektora iste dimenzije x 1 , x 2 ,...,x K i isti broj brojeva α α 1 , α 2 ,...,α K. Vector

y= α 1 x 1 + α 2 x 2 +...+α K x K

pozvao linearna kombinacija vektori x k .

Ako postoje takvi brojevi različiti od nule α k ≠ 0, k = 1,..., K, šta y = 0 , onda takav skup vektora x k pozvao linearno zavisna. Inače, vektori se nazivaju linearno nezavisni. Na primjer, vektori x 1 = (2, 2) t i x 2 = (−1, −1) t su linearno zavisne, jer x 1 +2x 2 = 0

1.13. Matrix rang

Razmotrite skup K vektori x 1 , x 2 ,...,x K dimenzije N. Rang ovog sistema vektora je maksimalni broj linearno nezavisnih vektora. Na primjer u kompletu

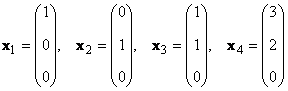
postoje samo dva linearno nezavisna vektora, na primjer x 1 i x 2, pa je njegov rang 2.

Očigledno, ako postoji više vektora u skupu od njihove dimenzije ( K>N), onda su oni nužno linearno zavisni.

Matrix rang(označeno rangom ( A)) je rang sistema vektora od kojih se sastoji. Iako se bilo koja matrica može predstaviti na dva načina (vektori stupaca ili vektori reda), to ne utiče na vrijednost ranga, jer

1.14. inverzna matrica

kvadratna matrica A naziva se nedegenerisanim ako ima jedinstvenu obrnuto matrica A-1 , utvrđeno uslovima

aa −1 = A −1 A = I.

Inverzna matrica ne postoji za sve matrice. Neophodan i dovoljan uslov za nedegeneraciju je

det( A) ≠ 0 ili rang ( A) = N.

Inverzija matrice je složena procedura za koju postoje posebni programi. Na primjer,

Rice. 17 Inverzija matrice

Dajemo formule za najjednostavniji slučaj - matrice 2 × 2

Ako matrice A i B su nedegenerisani, dakle

(AB) −1 = B −1 A −1 .

1.15. Pseudo-inverzna matrica

Ako je matrica A je degenerisana i inverzna matrica ne postoji, onda se u nekim slučajevima može koristiti pseudo-inverzno matrica, koja je definisana kao takva matrica A+ to

aa + A = A.

Pseudo-inverzna matrica nije jedina i njen oblik zavisi od načina konstrukcije. Na primjer, za pravokutnu matricu možete koristiti Moore-Penroseov metod.

Ako je broj kolona manji od broja redova, onda

A + =(A t A) −1 A t

Na primjer,

Rice. 17a Inverzija pseudo matrice

Ako je broj kolona veći od broja redova, onda

A + =A t( aa t) −1

1.16. Množenje vektora matricom

Vector x može se pomnožiti matricom A odgovarajuća dimenzija. U ovom slučaju, vektor stupca se množi na desnoj strani Sjekira, a vektorski niz je na lijevoj strani x t A. Ako je dimenzija vektora J, i dimenziju matrice I× J onda je rezultat vektor dimenzija I. Na primjer,

Rice. 18 Vektorsko-matrično množenje

Ako je matrica A- kvadratni ( I× I), zatim vektor y = Sjekira ima istu dimenziju kao x. Očigledno je da

A(α 1 x 1 + α 2 x 2) = α 1 Sjekira 1 + α 2 Sjekira 2 .

Stoga se matrice mogu posmatrati kao linearne transformacije vektora. Posebno x = x, Ox = 0 .

2. Dodatne informacije

2.1. Sistemi linearnih jednačina

Neka A- veličina matrice I× J, a b- vektor dimenzija J. Razmotrite jednačinu

Sjekira = b

u odnosu na vektor x, dimenzije I. U suštini, ovo je sistem I linearne jednačine With J nepoznato x 1 ,...,x J. Rješenje postoji ako i samo ako

rang ( A) = rang( B) = R,

gdje B je matrica proširene dimenzije I×( J+1) koji se sastoji od matrice A, podstavljena kolonom b, B = (A b). Inače, jednačine su nekonzistentne.

Ako R = I = J, onda je rješenje jedinstveno

x = A −1 b.

Ako R < I, tada postoji mnogo različitih rješenja koja se mogu izraziti u terminima linearne kombinacije J−R vektori. Sistem homogene jednačine Sjekira = 0 sa kvadratnom matricom A (N× N) Ima netrivijalno rešenje (x ≠ 0 ) ako i samo ako det( A) = 0. Ako R= rang( A)<N, onda postoje N−R linearno nezavisna rješenja.

2.2. Bilinearni i kvadratni oblici

Ako A je kvadratna matrica, i x i y- vektori odgovarajuće dimenzije, zatim skalarni proizvod forme x t Ay pozvao bilinearni oblik definisan matricom A. At x = y izraz x t Sjekira pozvao kvadratni formu.

2.3. Pozitivno određene matrice

kvadratna matrica A pozvao pozitivno definitivno, ako je za bilo koji vektor različit od nule x ≠ 0 ,

x t Sjekira > 0.

The negativan (x t Sjekira < 0), nenegativan (x t Sjekira≥ 0) i nepozitivna (x t Sjekira≤ 0) određene matrice.

2.4. Cholesky decomposition

Ako je simetrična matrica A je pozitivno određen, onda postoji jedinstvena trokutasta matrica U sa pozitivnim elementima, za koje

A = U t U.

Na primjer,

Rice. 19 Cholesky dekompozicija

2.5. polarna dekompozicija

Neka A je nedegenerirana kvadratna matrica dimenzija N× N. Zatim postoji jedinstvena polar reprezentacija

A = SR,

gdje S je nenegativna simetrična matrica, i R je ortogonalna matrica. matrice S i R može se eksplicitno definirati:

S 2 = aa t or S = (aa t) ½ i R = S −1 A = (aa t) −½ A.

Na primjer,

Rice. 20 Polarna dekompozicija

Ako je matrica A je degenerisan, onda dekompozicija nije jedinstvena - naime: S i dalje sam, ali R može biti mnogo. Polarna dekompozicija predstavlja matricu A kao kombinacija kompresije/rastezanja S i okretanje R.

2.6. Sopstveni vektori i sopstvene vrednosti

Neka A je kvadratna matrica. Vector v pozvao sopstveni vektor matrice A, ako

Av = λ v,

gdje se zove broj λ eigenvalue matrice A. Dakle, transformacija koju matrica izvodi A preko vektora v, se svodi na jednostavno rastezanje ili kompresiju s faktorom λ. Svojstveni vektor je određen do množenja konstantom α ≠ 0, tj. ako v je svojstveni vektor, onda je α v je takođe svojstveni vektor.

2.7. Svojstvene vrijednosti

Na matrici A, dimenzija ( N× N) ne može biti veći od N sopstvene vrijednosti. Oni zadovoljavaju karakteristična jednačina

det( A − λ I) = 0,

biće algebarska jednačina N-th red. Konkretno, za matricu 2×2 karakteristična jednačina ima oblik

Na primjer,

Rice. 21 Sopstvene vrijednosti

Skup svojstvenih vrijednosti λ 1 ,..., λ N matrice A pozvao spektra A.

Spektar ima različita svojstva. Posebno

det( A) = λ 1×...×λ N, Sp( A) = λ 1 +...+λ N.

Vlastite vrijednosti proizvoljne matrice mogu biti kompleksni brojevi, ali ako je matrica simetrična ( A t = A), tada su njegove vlastite vrijednosti realne.

2.8. Vlastiti vektori

Na matrici A, dimenzija ( N× N) ne može biti veći od N svojstvene vektore, od kojih svaki odgovara svojoj vrijednosti. Odrediti svojstveni vektor v n potrebno je da rešite sistem homogenih jednačina

(A − λ n I)v n = 0 .

Ima netrivijalno rješenje jer det( A-λ n I) = 0.

Na primjer,

Rice. 22 Sopstveni vektori

Svojstveni vektori simetrične matrice su ortogonalni.

Svojstvene vrijednosti (brojevi) i sopstveni vektori.
Primjeri rješenja

Budi svoj

Iz obje jednačine slijedi da .

Stavimo onda: .

Kao rezultat: je drugi sopstveni vektor.

Hajde da rezimiramo važne tačke:

– rezultirajući sistem svakako jeste zajednička odluka(jednadžbe su linearno zavisne);

- "Y" se bira na način da je cijeli broj, a prva "x" koordinata je cjelobrojna, pozitivna i što manja.

– provjeravamo da li određeno rješenje zadovoljava svaku jednačinu sistema.

Odgovori .

Međusobne "kontrolne tačke" bile su sasvim dovoljne, pa je provjera jednakosti, u principu, suvišna.

U različitim izvorima informacija, koordinate vlastitih vektora često se ne pišu u stupcima, već u redovima, na primjer: (i, da budem iskren, i sam sam ih pisao u redovima). Ova opcija je prihvatljiva, ali u svjetlu teme linearne transformacije tehnički praktičniji za upotrebu vektori stupaca.

Možda vam se rješenje učinilo dugim, ali to je samo zato što sam prvi primjer prokomentarisao vrlo detaljno.

Primjer 2

matrice

Treniramo sami! Približan uzorak konačnog dizajna zadatka na kraju lekcije.

Ponekad je potrebno dodatni zadatak, naime:

napišite kanonsku dekompoziciju matrice

Šta je to?

Ako se formiraju sopstveni vektori matrice osnovu, onda se može predstaviti kao:

Gdje je matrica sastavljena od koordinata vlastitih vektora, – dijagonala matrica s odgovarajućim svojstvenim vrijednostima.

Ova matrična dekompozicija se zove kanonski ili dijagonala.

Razmotrimo matricu prvog primjera. Njeni sopstveni vektori linearno nezavisna(nekolinearne) i čine osnovu. Napravimo matricu od njihovih koordinata:

On glavna dijagonala matrice po propisanom redu locirane su vlastite vrijednosti, a preostali elementi su jednaki nuli:
- još jednom naglašavam važnost reda: "dva" odgovara 1. vektoru i stoga se nalazi u 1. koloni, "tri" - 2. vektoru.

Prema uobičajenom algoritmu za pronalaženje inverzna matrica ili Gauss-Jordan metoda nađi . Ne, to nije greška u kucanju! - pred vama je rijedak događaj, poput pomračenja Sunca, kada se revers poklopio s originalnom matricom.

Ostaje napisati kanonsku dekompoziciju matrice:

Sistem se može riješiti sa elementarne transformacije a u sljedećim primjerima ćemo pribjeći ovoj metodi. Ali ovdje "školska" metoda radi mnogo brže. Iz 3. jednačine izražavamo: - zamjenu u drugu jednačinu:

Budući da je prva koordinata nula, dobijamo sistem , iz svake jednačine iz koje slijedi da .

I opet obratite pažnju na obavezno prisustvo linearnog odnosa. Ako se dobije samo trivijalno rješenje , tada je ili svojstvena vrijednost pogrešno pronađena, ili je sistem kompajliran / riješen s greškom.

Kompaktne koordinate daju vrijednost

Vlastiti vektor:

I još jednom provjeravamo da li je pronađeno rješenje zadovoljava svaku jednačinu sistema. U narednim paragrafima i narednim zadacima preporučujem da se ova želja prihvati kao obavezno pravilo.

2) Za svojstvenu vrijednost, slijedeći isti princip, dobijamo sljedeći sistem:

Iz 2. jednačine sistema izražavamo: - zamjenu u treću jednačinu:

Pošto je "zeta" koordinata jednaka nuli, dobijamo sistem , iz čije jednačine sledi linearna zavisnost.

Neka

Provjeravamo da li je rješenje zadovoljava svaku jednačinu sistema.

Dakle, sopstveni vektor: .

3) I, konačno, sistem odgovara vlastitoj vrijednosti:

Druga jednačina izgleda najjednostavnije, pa je iz nje izražavamo i zamjenjujemo u 1. i 3. jednadžbu:

Sve je u redu - otkrivena je linearna ovisnost koju zamjenjujemo u izraz:

Kao rezultat, "X" i "Y" su izraženi kroz "Z": . U praksi nije potrebno postići samo takve odnose, u nekim slučajevima je zgodnije izraziti i kroz ili i kroz . Ili čak "voz" - na primjer, "X" do "Y", i "Y" do "Z"

Stavimo onda:

Provjeravamo da li je pronađeno rješenje zadovoljava svaku jednačinu sistema i napiše treći svojstveni vektor

Odgovori: sopstveni vektori:

Geometrijski, ovi vektori definiraju tri različita prostorna pravca ("Tamo i nazad"), prema kojoj linearna transformacija transformira vektore različite od nule (svojstvene vektore) u vektore kolinearne njima.

Ako je po uvjetu bilo potrebno pronaći kanonsku ekspanziju od , onda je to moguće ovdje, jer različite vlastite vrijednosti odgovaraju različitim linearno nezavisnim svojstvenim vektorima. Pravimo matricu iz njihovih koordinata, dijagonalna matrica od relevantan svojstvene vrijednosti i nađi inverzna matrica .

Ako je prema uslovu potrebno napisati matrica linearne transformacije u bazi sopstvenih vektora, onda dajemo odgovor u obliku . Postoji razlika, i to značajna razlika! Za ovu matricu je matrica "de".

Zadatak s jednostavnijim proračunima za samostalno rješenje:

Primjer 5

Naći svojstvene vektore linearne transformacije date matricom

Prilikom pronalaženja vlastitih brojeva, pokušajte ne dovesti slučaj do polinoma 3. stepena. Osim toga, vaša sistemska rješenja mogu se razlikovati od mojih rješenja – ovdje nema jednoznačnosti; a vektori koje pronađete mogu se razlikovati od vektora uzorka do proporcionalnosti njihovim odgovarajućim koordinatama. Na primjer, i . Estetski je odgovornije predstaviti u obliku , ali je u redu ako se zaustavite na drugoj opciji. Međutim, postoje razumna ograničenja za sve, verzija više ne izgleda baš dobro.

Okvirni konačni uzorak zadatka na kraju lekcije.

Kako riješiti problem u slučaju više vlastitih vrijednosti?

Opšti algoritam ostaje isti, ali ima svoje posebnosti, te je preporučljivo zadržati neke dijelove rješenja u rigoroznijem akademskom stilu:

Primjer 6

Pronađite svojstvene vrijednosti i svojstvene vektore

Odluka

Naravno, pišemo velikim slovom fantastičnu prvu kolonu:

I, nakon faktoringa kvadratnog trinoma:

Kao rezultat, dobivaju se vlastite vrijednosti, od kojih su dvije višekratne.

Nađimo sopstvene vektore:

1) Postupit ćemo sa usamljenim vojnikom prema „pojednostavljenoj“ šemi:

Iz posljednje dvije jednačine jasno je vidljiva jednakost koju, očigledno, treba zamijeniti 1. jednačinom sistema:

Nema bolje kombinacije:
Vlastiti vektor:

2-3) Sada uklanjamo nekoliko stražara. U ovom slučaju može biti ili dva ili jedan svojstveni vektor. Bez obzira na višestrukost korijena, vrijednost zamjenjujemo u determinanti , što nam donosi sljedeće homogeni sistem linearnih jednačina:

Svojstveni vektori su upravo vektori
fundamentalni sistem odlučivanja

Zapravo, tokom čitave lekcije samo smo se bavili pronalaženjem vektora fundamentalnog sistema. Samo za sada ovaj termin nije bio posebno potreban. Uzgred, oni spretni studenti koji, u kamuflaži homogene jednačine, biće primoran da ga sada popuši.

Jedina akcija bila je uklanjanje dodatnih linija. Rezultat je "jedan po tri" matrica sa formalnim "korakom" u sredini.
– osnovna varijabla, – slobodne varijable. Postoje dvije slobodne varijable, dakle postoje i dva vektora fundamentalnog sistema.

Izrazimo osnovnu varijablu u terminima slobodnih varijabli: . Nulti faktor ispred "x" omogućava mu da preuzme apsolutno bilo koje vrijednosti (što je također jasno vidljivo iz sistema jednadžbi).

U kontekstu ovog problema, prikladnije je opće rješenje napisati ne u redu, već u stupcu:

Par odgovara sopstvenom vektoru:
Par odgovara sopstvenom vektoru:

Bilješka : sofisticirani čitaoci mogu da pokupe ove vektore usmeno - samo analizom sistema , ali ovdje je potrebno određeno znanje: postoje tri varijable, rang sistemske matrice- jedinična sredstva fundamentalni sistem odlučivanja sastoji se od 3 – 1 = 2 vektora. Međutim, pronađeni vektori su savršeno vidljivi i bez ovog znanja, čisto na intuitivnom nivou. U ovom slučaju, treći vektor će biti napisan još „ljepše“: . Međutim, upozoravam, u drugom primjeru možda nema jednostavnog odabira, zbog čega je rezervacija namijenjena iskusnim osobama. Osim toga, zašto ne uzeti kao treći vektor, recimo, ? Na kraju krajeva, njegove koordinate također zadovoljavaju svaku jednačinu sistema i vektore su linearno nezavisne. Ova opcija je, u principu, prikladna, ali "kriva", budući da je "drugi" vektor linearna kombinacija vektora osnovnog sistema.

Odgovori: vlastite vrijednosti: , svojstveni vektori:

Sličan primjer za "uradi sam" rješenje:

Primjer 7

Pronađite svojstvene vrijednosti i svojstvene vektore

Približan uzorak završne obrade na kraju lekcije.

Treba napomenuti da se i u 6. i u 7. primjeru dobija trojka linearno nezavisnih svojstvenih vektora, pa se stoga originalna matrica može predstaviti u kanonskom proširenju. Ali takve maline se ne dešavaju u svim slučajevima:

Primjer 8

Odluka: sastaviti i riješiti karakterističnu jednačinu:

Proširujemo determinantu za prvi stupac:

Dalja pojednostavljenja vršimo prema razmatranoj metodi, izbjegavajući polinom 3. stepena:

su sopstvene vrijednosti.

Nađimo sopstvene vektore:

1) Nema poteškoća s root-om:

Nemojte se iznenaditi, osim kompleta, u upotrebi su i varijable - tu nema razlike.

Iz 3. jednačine izražavamo - zamjenjujemo u 1. i 2. jednačinu:

Iz obje jednačine slijedi:

Neka onda:

2-3) Za više vrijednosti dobijamo sistem .

Zapišimo matricu sistema i, koristeći elementarne transformacije, dovedemo je u stepenasti oblik:

Svojstveni vektor kvadratne matrice je onaj koji, kada se pomnoži sa datom matricom, rezultira kolinearnim vektorom. Jednostavnim riječima, kada se matrica pomnoži s vlastitim vektorom, potonji ostaje isti, ali pomnožen nekim brojem.

Definicija

Svojstveni vektor je vektor V koji nije nula, koji, kada se pomnoži kvadratnom matricom M, postaje sam, uvećan za neki broj λ. U algebarskoj notaciji ovo izgleda ovako:

M × V = λ × V,

gdje je λ vlastita vrijednost matrice M.

Razmotrimo numerički primjer. Radi lakšeg pisanja, brojevi u matrici će biti odvojeni tačkom i zarezom. Recimo da imamo matricu:

• M = 0; četiri;
• 6; 10.

Pomnožimo ga vektorom stupca:

• V = -2;

Kada množimo matricu vektorom kolone, dobijamo i vektor kolone. U strogom matematičkom jeziku, formula za množenje matrice 2 × 2 vektorom kolone bi izgledala ovako:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 označava element matrice M koji stoji u prvom redu i prvoj koloni, a M22 je element koji se nalazi u drugom redu i drugoj koloni. Za našu matricu ovi elementi su M11 = 0, M12 = 4, M21 = 6, M22 10. Za vektor stupac ove vrijednosti su V11 = –2, V21 = 1. Prema ovoj formuli dobijamo sljedeće rezultat proizvoda kvadratne matrice vektorom:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Radi praktičnosti, pišemo vektor kolone u red. Dakle, kvadratnu matricu smo pomnožili sa vektorom (-2; 1), što je rezultiralo vektorom (4; -2). Očigledno, ovo je isti vektor pomnožen sa λ = -2. Lambda u ovom slučaju označava sopstvenu vrijednost matrice.

Vlastiti vektor matrice je kolinearni vektor, odnosno objekt koji ne mijenja svoj položaj u prostoru kada se pomnoži sa matricom. Koncept kolinearnosti u vektorskoj algebri sličan je terminu paralelizma u geometriji. U geometrijskoj interpretaciji, kolinearni vektori su paralelno usmjereni segmenti različitih dužina. Još od Euklidovog vremena znamo da jedna linija ima beskonačan broj linija paralelnih sa njom, pa je logično pretpostaviti da svaka matrica ima beskonačan broj svojstvenih vektora.

Iz prethodnog primjera može se vidjeti da oba (-8; 4), i (16; -8), i (32, -16) mogu biti svojstveni vektori. Sve su to kolinearni vektori koji odgovaraju svojstvenoj vrijednosti λ = -2. Kada množimo originalnu matricu ovim vektorima, i dalje ćemo dobiti vektor kao rezultat, koji se razlikuje od originalne 2 puta. Zato je pri rješavanju zadataka za pronalaženje svojstvenog vektora potrebno pronaći samo linearno nezavisne vektorske objekte. Najčešće, za n × n matricu, postoji n-ti broj sopstvenih vektora. Naš kalkulator je dizajniran za analizu kvadratnih matrica drugog reda, tako da će se gotovo uvijek kao rezultat naći dva svojstvena vektora, osim kada se poklapaju.

U gornjem primjeru, unaprijed smo znali svojstveni vektor originalne matrice i vizualno odredili lambda broj. Međutim, u praksi se sve događa obrnuto: na početku su svojstvene vrijednosti pa tek onda svojstveni vektori.

Algoritam rješenja

Pogledajmo ponovo originalnu matricu M i pokušajmo pronaći oba njena svojstvena vektora. Dakle, matrica izgleda ovako:

• M = 0; četiri;
• 6; 10.

Za početak, moramo odrediti svojstvenu vrijednost λ, za koju trebamo izračunati determinantu sljedeće matrice:

• (0 − λ); četiri;
• 6; (10 − λ).

Ova matrica dobijeno oduzimanjem nepoznatog λ od elemenata na glavnoj dijagonali. Determinanta je određena standardnom formulom:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Pošto naš vektor ne smije biti nula, uzimamo rezultirajuću jednačinu kao linearno zavisnu i izjednačavamo našu determinantu detA sa nulom.

(0 − λ) × (10 − λ) − 24 = 0

Otvorimo zagrade i dobijemo karakterističnu jednačinu matrice:

λ 2 − 10λ − 24 = 0

Ovo je standardno kvadratna jednačina, koji se rješava u smislu diskriminanta.

D \u003d b 2 - 4ac = (-10) × 2 - 4 × (-1) × 24 = 100 + 96 \u003d 196

Koren diskriminante je sqrt(D) = 14, tako da je λ1 = -2, λ2 = 12. Sada za svaku lambda vrijednost, moramo pronaći svojstveni vektor. Izrazimo koeficijente sistema za λ = -2.

• M − λ × E = 2; četiri;
• 6; 12.

U ovoj formuli, E je matrica identiteta. Na osnovu dobijene matrice sastavljamo sistem linearnih jednadžbi:

2x + 4y = 6x + 12y

gdje su x i y elementi sopstvenog vektora.

Skupimo sve X na lijevoj i sve Y na desnoj strani. Očigledno - 4x = 8y. Podijelite izraz sa -4 i dobijete x = -2y. Sada možemo odrediti prvi svojstveni vektor matrice uzimanjem bilo koje vrijednosti nepoznatih (sjetite se beskonačnosti linearno zavisnih svojstvenih vektora). Uzmimo y = 1, a zatim x = -2. Dakle, prvi sopstveni vektor izgleda kao V1 = (–2; 1). Vratite se na početak članka. Upravo smo ovim vektorskim objektom pomnožili matricu da bismo demonstrirali koncept svojstvenog vektora.

Sada pronađimo svojstveni vektor za λ = 12.

• M - λ × E = -12; četiri
• 6; -2.

Sastavimo isti sistem linearnih jednačina;

• -12x + 4y = 6x − 2y
• -18x = -6y
• 3x=y.

Uzmimo sada x = 1, dakle y = 3. Dakle, drugi svojstveni vektor izgleda kao V2 = (1; 3). Prilikom množenja originalne matrice ovim vektorom, rezultat će uvijek biti isti vektor pomnožen sa 12. Ovim se završava algoritam rješenja. Sada znate kako ručno definirati svojstveni vektor matrice.

• determinanta;
• trag, odnosno zbir elemenata na glavnoj dijagonali;
• rang, tj. maksimalni broj linearno nezavisnih redova/kolona.

Program radi prema gore navedenom algoritmu, minimizirajući proces rješenja. Važno je istaći da se u programu lambda označava slovom "c". Pogledajmo brojčani primjer.

Primjer programa

Pokušajmo definirati svojstvene vektore za sljedeću matricu:

• M=5; 13;
• 4; 14.

Unesimo ove vrijednosti u ćelije kalkulatora i dobijemo odgovor u sljedećem obliku:

• Rang matrice: 2;
• Matrična determinanta: 18;
• Trag matrice: 19;
• Proračun sopstvenog vektora: c 2 − 19.00c + 18.00 (jednačina karakteristike);
• Izračun sopstvenog vektora: 18 (prva lambda vrijednost);
• Izračun sopstvenog vektora: 1 (druga lambda vrijednost);
• Sistem jednačina vektora 1: -13x1 + 13y1 = 4x1 − 4y1;
• Sistem jednadžbi vektora 2: 4x1 + 13y1 = 4x1 + 13y1;
• Vlastiti vektor 1: (1; 1);
• Vlastiti vektor 2: (-3,25; 1).

Tako smo dobili dva linearno nezavisna svojstvena vektora.

Zaključak

Linearna algebra i analitička geometrija- standardni predmeti za svakog brucoša tehničke specijalnosti. Veliki broj vektori i matrice je zastrašujuća, i lako je pogriješiti u takvim glomaznim proračunima. Naš program će omogućiti studentima da provjere svoje proračune ili automatski riješe problem pronalaženja svojstvenog vektora. U našem katalogu postoje i drugi kalkulatori linearne algebre, koristite ih u svom učenju ili poslu.

Sa matricom A, ako postoji broj l takav da je AX = lX.

U ovom slučaju se poziva broj l eigenvalue operator (matrica A) koji odgovara vektoru X.

Drugim riječima, svojstveni vektor je vektor koji se pod djelovanjem linearnog operatora pretvara u kolinearni vektor, tj. samo pomnoži sa nekim brojem. Nasuprot tome, nepravilne vektore je teže transformisati.

Zapisujemo definiciju svojstvenog vektora kao sistema jednačina:

Pomerimo sve pojmove na lijevu stranu:

Poslednji sistem se može napisati u matričnom obliku na sledeći način:

(A - lE)X \u003d O

Rezultirajući sistem uvijek ima nulto rješenje X = O. Takvi sistemi u kojima su svi slobodni članovi jednaki nuli nazivaju se homogena. Ako je matrica takvog sistema kvadratna, a njena determinanta nije jednaka nuli, onda ćemo prema Cramerovim formulama uvijek dobiti jedinstveno rješenje - nulu. Može se dokazati da sistem ima rješenja različita od nule ako i samo ako je determinanta ove matrice jednaka nuli, tj.

|A - lE| = = 0

Ova jednačina sa nepoznatim l naziva se karakteristična jednačina (karakteristični polinom) matrica A (linearni operator).

Može se dokazati da karakteristični polinom linearnog operatora ne zavisi od izbora baze.

Na primjer, pronađimo svojstvene vrijednosti i svojstvene vektore linearnog operatora date matricom A =.

Da bismo to uradili, sastavljamo karakterističnu jednačinu |A - lE| = \u003d (1 - l) 2 - 36 \u003d 1 - 2l + l 2 - 36 \u003d l 2 - 2l - 35 \u003d 0; D \u003d 4 + 140 \u003d 144; sopstvene vrijednosti l 1 = (2 - 12)/2 = -5; l 2 = (2 + 12) / 2 = 7.

Da bismo pronašli svojstvene vektore, rješavamo dva sistema jednačina

(A + 5E) X = O

(A - 7E) X = O

Za prvi od njih, proširena matrica će poprimiti oblik

,

odakle je x 2 = c, x 1 + (2/3) c = 0; x 1 \u003d - (2/3) s, tj. X (1) \u003d (- (2/3) s; s).

Za drugu od njih, proširena matrica će poprimiti oblik

,

odakle je x 2 = c 1, x 1 - (2/3) c 1 = 0; x 1 = (2/3) s 1, tj. X (2) \u003d ((2/3) s 1; s 1).

Dakle, svojstveni vektori ovog linearnog operatora su svi vektori oblika (-(2/3)c; c) sa svojstvenom vrijednošću (-5) i svi vektori oblika ((2/3)c 1 ; c 1) sa svojstvena vrijednost 7 .

Može se dokazati da je matrica operatora A u bazi koju čine njegovi vlastiti vektori dijagonalna i ima oblik:

,

gdje su l i vlastite vrijednosti ove matrice.

Vrijedi i obrnuto: ako je matrica A u nekoj bazi dijagonalna, tada će svi vektori ove baze biti svojstveni vektori ove matrice.

Također se može dokazati da ako linearni operator ima n parno različitih svojstvenih vrijednosti, tada su odgovarajući svojstveni vektori linearno nezavisni, a matrica ovog operatora u odgovarajućoj bazi ima dijagonalni oblik.

Objasnimo ovo prethodnim primjerom. Uzmimo proizvoljne vrijednosti c i c 1 koje nisu nula, ali takve da su vektori X (1) i X (2) linearno nezavisni, tj. predstavljalo bi osnovu. Na primjer, neka je c \u003d c 1 = 3, zatim X (1) = (-2; 3), X (2) = (2; 3).

Hajde da se uverimo linearnu nezavisnost ovi vektori:

12 ≠ 0. U ovoj novoj bazi, matrica A će imati oblik A * = .

Da bismo to potvrdili, koristimo formulu A * = C -1 AC. Nađimo prvo C -1.

C -1 = ;

Kvadratni oblici

kvadratni oblik f (x 1, x 2, x n) od n varijabli naziva se zbir, čiji je svaki član ili kvadrat jedne od varijabli, ili proizvod dvije različite varijable, uzete sa određenim koeficijentom: f (x 1 , x 2, x n) = (a ij = a ji).

Matrica A, sastavljena od ovih koeficijenata, naziva se matrica kvadratni oblik. Uvek je tako simetrično matrica (tj. matrica simetrična oko glavne dijagonale, a ij = a ji).

U matričnom zapisu, kvadratni oblik ima oblik f(X) = X T AX, gdje je

Zaista

Na primjer, zapišimo kvadratni oblik u matričnom obliku.

Da bismo to učinili, nalazimo matricu kvadratnog oblika. Njegovi dijagonalni elementi jednaki su koeficijentima na kvadratima varijabli, a preostali elementi jednaki su polovini odgovarajućih koeficijenata kvadratnog oblika. dakle

Neka se matrični stupac varijabli X dobije nedegeneriranom linearnom transformacijom matrice-kolone Y, tj. X = CY, gdje je C nedegenerirana matrica reda n. Tada je kvadratni oblik f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y.

Dakle, pod nedegeneriranom linearnom transformacijom C, matrica kvadratnog oblika ima oblik: A * = C T AC.

Na primjer, pronađimo kvadratni oblik f(y 1, y 2) dobijen iz kvadratnog oblika f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 linearnom transformacijom.

Kvadratni oblik se zove kanonski(Ima kanonski pogled) ako su svi njegovi koeficijenti a ij = 0 za i ≠ j, tj.
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =.

Njegova matrica je dijagonalna.

Teorema(dokaz ovdje nije dat). Bilo koji kvadratni oblik može se svesti na kanonski oblik korištenjem nedegenerirane linearne transformacije.

Na primjer, svodimo na kanonski oblik kvadratni oblik
f (x 1, x 2, x 3) \u003d 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3.

Da biste to učinili, prvo odaberite cijeli kvadrat za varijablu x 1:

f (x 1, x 2, x 3) = 2 (x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 \u003d 2 (x 1 + x 2 ) 2 - 5x 2 2 - x 2 x 3.

Sada biramo puni kvadrat za varijablu x 2:

f (x 1, x 2, x 3) \u003d 2 (x 1 + x 2) 2 - 5 (x 2 2 + 2 * x 2 * (1/10) x 3 + (1/100) x 3 2 ) + (5/100) x 3 2 =
\u003d 2 (x 1 + x 2) 2 - 5 (x 2 - (1/10) x 3) 2 + (1/20) x 3 2.

Tada nedegenerirana linearna transformacija y 1 = x 1 + x 2, y 2 = x 2 + (1/10) x 3 i y 3 = x 3 dovodi ovaj kvadratni oblik u kanonski oblik f (y 1 , y 2, y 3) = 2y 1 2 - 5y 2 2 + (1/20)y 3 2 .

Imajte na umu da je kanonski oblik kvadratnog oblika definiran dvosmisleno (isti kvadratni oblik se može svesti na kanonski oblik na različite načine). Međutim, the Različiti putevi kanonski oblici imaju niz zajedničkih svojstava. Konkretno, broj članova s ​​pozitivnim (negativnim) koeficijentima kvadratnog oblika ne ovisi o tome kako se oblik svodi na ovaj oblik (na primjer, u razmatranom primjeru uvijek će postojati dva negativna i jedan pozitivan koeficijent). Ovo svojstvo se zove zakon inercije kvadratnih oblika.

Provjerimo ovo tako što ćemo isti kvadratni oblik na drugačiji način svesti na kanonski oblik. Započnimo transformaciju s varijablom x 2:

f (x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 \u003d -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 \u003d - 3(x 2 2 +
+ 2 * x 2 ((1/6) x 3 - (2/3) x 1) + ((1/6) x 3 - (2/3) x 1) 2) + 3 ((1/6) x 3 - (2/3) x 1) 2 + 2x 1 2 =
\u003d -3 (x 2 + (1/6) x 3 - (2/3) x 1) 2 + 3 ((1/6) x 3 + (2/3) x 1) 2 + 2x 1 2 \ u003d f (y 1, y 2, y 3) = -3y 1 2 -
+ 3y 2 2 + 2y 3 2, gdje je y 1 \u003d - (2/3) x 1 + x 2 + (1/6) x 3, y 2 = (2/3) x 1 + (1/6 ) x 3 i y 3 = x 1 . Ovdje su negativni koeficijent -3 na y 1 i dva pozitivna koeficijenta 3 i 2 na y 2 i y 3 (a koristeći drugu metodu, dobili smo negativan koeficijent (-5) na y 2 i dva pozitivna koeficijenta: 2 na y 1 i 1/20 za y 3).

Također treba napomenuti da je rang matrice kvadratnog oblika, tzv rang kvadratnog oblika, jednak je broju nenultih koeficijenata kanonskog oblika i ne mijenja se pod linearnim transformacijama.

Kvadratni oblik f(X) se zove pozitivno (negativan) siguran, ako je za sve vrijednosti varijabli koje nisu istovremeno jednake nuli, ono je pozitivno, tj. f(X) > 0 (negativno, tj.
f(X)< 0).

Na primjer, kvadratni oblik f 1 (X) \u003d x 1 2 + x 2 2 je pozitivno određen, jer je zbir kvadrata, a kvadratni oblik f 2 (X) \u003d -x 1 2 + 2x 1 x 2 - x 2 2 je negativno određen, jer predstavlja može se predstaviti kao f 2 (X) \u003d - (x 1 - x 2) 2.

U većini praktičnih situacija je nešto teže utvrditi predznačnu određenost kvadratnog oblika, pa se za to koristi jedna od sljedećih teorema (formuliramo ih bez dokaza).

Teorema. Kvadratni oblik je pozitivno (negativno) određen ako i samo ako su sve vlastite vrijednosti njegove matrice pozitivne (negativne).

Teorema(Sylvesterov kriterijum). Kvadratni oblik je pozitivno određen ako i samo ako su svi glavni minori matrice ovog oblika pozitivni.

Dur (ugao) mol K-ti red matrice A n-tog reda naziva se determinanta matrice, sastavljena od prvih k redova i stupaca matrice A ().

Imajte na umu da se za negativno-definirane kvadratne forme predznaci glavnih minora izmjenjuju, a minor prvog reda mora biti negativan.

Na primjer, ispitujemo kvadratni oblik f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 za predznak-određenost.

= (2 - l)*
*(3 - l) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 \u003d 0; D = 25 - 8 = 17;
. Stoga je kvadratni oblik pozitivno određen.

Metoda 2. Glavni minor prvog reda matrice A D 1 = a 11 = 2 > 0. Glavni minor drugog reda D 2 = = 6 - 4 = 2 > 0. Prema tome, prema Sylvesterovom kriteriju, kvadratni oblik je pozitivno određen.

Ispitujemo još jedan kvadratni oblik za znak-definiranost, f (x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2.

Metoda 1. Konstruirajmo matricu kvadratnog oblika A = . Karakteristična jednačina će imati oblik = (-2 - l)*
*(-3 - l) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; D = 25 - 8 = 17;
. Stoga je kvadratni oblik negativno određen.

Metoda 2. Glavni minor prvog reda matrice A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. Dakle, prema Sylvesterovom kriteriju, kvadratni oblik je negativno određen (znaci glavnih minora se izmjenjuju, počevši od minusa).

I kao još jedan primjer, ispitujemo kvadratni oblik f (x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 za predznak.

Metoda 1. Konstruirajmo matricu kvadratnog oblika A = . Karakteristična jednačina će imati oblik = (2 - l)*
*(-3 - l) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; D = 1 + 40 = 41;
.

Jedan od ovih brojeva je negativan, a drugi pozitivan. Znaci sopstvenih vrednosti su različiti. Dakle, kvadratni oblik ne može biti ni negativan ni pozitivno određen, tj. ovaj kvadratni oblik nije znakom određen (može uzeti vrijednosti bilo kojeg predznaka).

Metoda 2. Glavni minor prvog reda matrice A D 1 = a 11 = 2 > 0. Glavni minor drugog reda D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

Definicija 9.3. Vector X pozvao sopstveni vektor matrice I ako postoji takav broj λ, da vrijedi jednakost: I X= λ X, odnosno rezultat prijave na X linearnu transformaciju datu matricom I, je množenje ovog vektora brojem λ . Sam broj λ pozvao sopstveni broj matrice I.

Zamjena u formule (9.3) x` j = λx j , dobijamo sistem jednadžbi za određivanje koordinata sopstvenog vektora:

. (9.5)

Ovaj linearni homogeni sistem će imati netrivijalno rješenje samo ako mu je glavna determinanta 0 (Kramerovo pravilo). Pisanjem ovog uslova u obliku:

dobijamo jednačinu za određivanje sopstvenih vrednosti λ pozvao karakteristična jednačina. Ukratko, može se predstaviti na sljedeći način:

| A-λE | = 0, (9.6)

pošto je njegova lijeva strana determinanta matrice A-λE. Polinom u odnosu na λ | A-λE| pozvao karakteristični polinom matrice a.

Svojstva karakterističnog polinoma:

1) Karakteristični polinom linearne transformacije ne zavisi od izbora baze. Dokaz. (vidi (9.4)), ali Shodno tome, . Dakle, ne zavisi od izbora osnove. Dakle, i | A-λE| ne mijenja se pri prelasku na novu osnovu.

2) Ako je matrica I linearna transformacija je simetrično(oni. a ij = a ji), tada su svi korijeni karakteristične jednadžbe (9.6) realni brojevi.

Svojstva sopstvenih vrednosti i sopstvenih vektora:

1) Ako odaberemo osnovu od sopstvenih vektora x 1, x 2, x 3 koji odgovaraju sopstvenim vrednostima λ 1 , λ 2 , λ 3 matrice I, tada u ovoj osnovi linearna transformacija A ima dijagonalnu matricu:

(9.7) Dokaz ovog svojstva slijedi iz definicije svojstvenih vektora.

2) Ako je transformacija svojstvene vrijednosti I su različiti, onda su svojstveni vektori koji im odgovaraju linearno nezavisni.

3) Ako je karakterističan polinom matrice I ima tri različita korijena, onda u nekoj osnovi matrica I ima dijagonalni oblik.

Nađimo svojstvene vrijednosti i svojstvene vektore matrice Napravimo karakterističnu jednačinu: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Pronađite koordinate svojstvenih vektora koji odgovaraju svakoj pronađenoj vrijednosti λ. Iz (9.5) slijedi da ako X (1) ={x 1 , x 2 , x 3) je svojstveni vektor koji odgovara λ 1 = -2, onda

je kolaborativni, ali neodređen sistem. Njegovo rješenje se može zapisati kao X (1) ={a,0,-a), gdje je a bilo koji broj. Posebno, ako to zahtijevate | x (1) |=1, X (1) =

Zamjena u sistem (9.5) λ 2 =3, dobijamo sistem za određivanje koordinata drugog sopstvenog vektora - x (2) ={y1,y2,y3}:

, gdje X (2) ={b,-b,b) ili, pod uslovom | x (2) |=1, x (2) =

Za λ 3 = 6 pronađite svojstveni vektor x (3) ={z1, z2, z3}:

, x (3) ={c,2c,c) ili u normaliziranoj verziji

x (3) = To se vidi X (1) X (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = bc- 2bc + bc= 0. Dakle, svojstveni vektori ove matrice su po paru ortogonalni.

Predavanje 10

Kvadratni oblici i njihova povezanost sa simetričnim matricama. Svojstva svojstvenih vektora i svojstvenih vrijednosti simetrične matrice. Redukcija kvadratnog oblika na kanonski oblik.

Definicija 10.1.kvadratni oblik realne varijable x 1, x 2,…, x n naziva se polinom drugog stepena u odnosu na ove varijable, koji ne sadrži slobodni član i članove prvog stepena.

Primjeri kvadratnih oblika:

(n = 2),

(n = 3). (10.1)

Prisjetimo se definicije simetrične matrice date u prošlom predavanju:

Definicija 10.2. Kvadratna matrica se zove simetrično, ako , odnosno ako su elementi matrice simetrični u odnosu na glavnu dijagonalu jednaki.

Svojstva svojstvenih vrijednosti i svojstvenih vektora simetrične matrice:

1) Sve vlastite vrijednosti simetrične matrice su realne.

Dokaz (za n = 2).

Pustite matricu I izgleda kao: . Napravimo karakterističnu jednačinu:

(10.2) Pronađite diskriminanta:

Dakle, jednadžba ima samo realne korijene.

2) Vlastiti vektori simetrične matrice su ortogonalni.

Dokaz (za n= 2).

Koordinate sopstvenih vektora i moraju zadovoljiti jednačine.