Příklad řešení rozptylu v rámci skupiny. Příklad hledání rozptylu

Pro seskupená data zbytkový rozptyl- průměr vnitroskupinových rozptylů:

Kde σ 2 j je vnitroskupinový rozptyl j-té skupiny.

Pro neseskupená data zbytkový rozptyl– míra aproximační přesnosti, tzn. aproximace regresní přímky k původním datům:
kde y(t) – předpověď podle trendové rovnice; y t – počáteční dynamická řada; n – počet bodů; p – počet koeficientů regresní rovnice (počet vysvětlujících proměnných).
V tomto příkladu se nazývá nezaujatý odhad rozptylu.

Příklad č. 1. Rozdělení pracovníků tří podniků jednoho sdružení podle tarifních kategorií charakterizují následující údaje:

Pracovní tarifní kategorie	Počet pracovníků v podniku
	podnik 1	podnik 2	podnik 3
1	50	20	40
2	100	80	60
3	150	150	200
4	350	300	400
5	200	150	250
6	150	100	150

Definovat:
1. rozptyl pro každý podnik (vnitroskupinové rozptyly);
2. průměr rozptylů v rámci skupiny;
3. meziskupinová disperze;
4. celkový rozptyl.

Řešení.
Před zahájením řešení problému je nutné zjistit, která funkce je účinná a která faktoriální. V uvažovaném příkladu je výsledný atribut „Kategorie tarifu“ a atribut faktoru „Číslo (název) podniku“.
Pak máme tři skupiny (podniky), pro které je nutné vypočítat skupinový průměr a vnitroskupinové rozptyly:

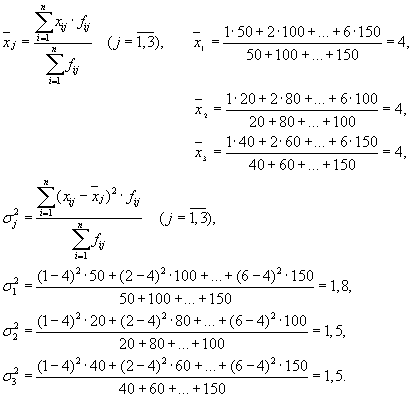
Podnik	průměr skupiny,	Rozdíl v rámci skupiny,
1	4	1,8

Průměr rozptylů v rámci skupiny ( zbytkový rozptyl) se vypočítá pomocí vzorce:

kde můžete počítat:
nebo:

Pak:
Celkový rozptyl se bude rovnat: s2 = 1,6 + 0 = 1,6.
Celkový rozptyl lze také vypočítat pomocí jednoho z následujících dvou vzorců:

Při řešení praktických problémů se člověk často musí vypořádat s rysem, který nabývá pouze dvou alternativních hodnot. V tomto případě nehovoříme o váze konkrétní hodnoty prvku, ale o jeho podílu na celku. Pokud je podíl populačních jednotek majících studovanou charakteristiku označen jako „ r", a ti, kteří nemají - přes" q", pak lze rozptyl vypočítat pomocí vzorce:
s2 = p×q

Příklad č. 2. Na základě výrobních dat šesti pracovníků v týmu určete meziskupinový rozptyl a vyhodnoťte dopad pracovní směny na jejich produktivitu práce, pokud je celkový rozptyl 12,2.

Týmový pracovník č.	Pracovní výkon, ks.
	v první směně	ve druhé směně
1	18	13
2	19	14
3	22	15
4	20	17
5	24	16
6	23	15

Řešení. Počáteční údaje

X	f 1	f 2	f 3	f 4	f 5	f 6	Celkový
1	18	19	22	20	24	23	126
2	13	14	15	17	16	15	90
Celkový	31	33	37	37	40	38

Pak máme 6 skupin, pro které je nutné vypočítat skupinový průměr a vnitroskupinové rozptyly.
1. Najděte průměrné hodnoty každé skupiny.







2. Najděte střední čtverec každé skupiny.







Shrňme výsledky výpočtu do tabulky:

Číslo skupiny	Skupinový průměr	Rozptyl v rámci skupiny
1	1.42	0.24
2	1.42	0.24
3	1.41	0.24
4	1.46	0.25
5	1.4	0.24
6	1.39	0.24

3. Rozptyl v rámci skupiny charakterizuje změnu (variaci) studované (výsledné) charakteristiky v rámci skupiny pod vlivem všech faktorů na ni, kromě faktoru, který je základem seskupení:
Průměr vnitroskupinových rozptylů vypočítáme pomocí vzorce:


4. Meziskupinová odchylka charakterizuje změnu (variaci) studované (výsledné) charakteristiky pod vlivem faktoru (faktorové charakteristiky), který tvoří základ skupiny.
Meziskupinový rozptyl definujeme jako:

Kde


Pak

Celkový rozptyl charakterizuje změnu (variaci) studované (výsledné) charakteristiky pod vlivem všech faktorů (faktorových charakteristik) bez výjimky. Podle podmínek problému se rovná 12.2.
Empirický korelační vztah měří, jaká část celkové variability výsledné charakteristiky je způsobena studovaným faktorem. Toto je poměr rozptylu faktorů k celkovému rozptylu:

Definujeme empirický korelační vztah:

Spojení mezi charakteristikami může být slabé a silné (těsné). Jejich kritéria jsou hodnocena podle Chaddockovy stupnice:
0,1 0,3 0,5 0,7 0,9 V našem příkladu je vztah mezi znakem Y a faktorem X slabý
Koeficient determinace.

Pojďme určit koeficient determinace:

0,67 % variace je tedy způsobeno rozdíly mezi vlastnostmi a 99,37 % je způsobeno jinými faktory.
Závěr: v tomto případě výkon pracovníků nezávisí na práci na konkrétní směně, tzn. vliv směny na jejich produktivitu práce není významný a je dán jinými faktory.

Příklad č. 3. Na základě průměru mzdy a druhé mocniny odchylek od jeho hodnoty pro dvě skupiny pracovníků, najděte celkový rozptyl použitím pravidla sčítání rozptylů:

Řešení:
Průměr rozptylů v rámci skupiny

Meziskupinový rozptyl definujeme jako:


Celkový rozptyl bude: 480 + 13824 = 14304

.

Naopak, pokud je nezáporné a.e. fungovat tak, že , pak existuje absolutně spojitá pravděpodobnostní míra na takové, že je to její hustota.

Nahrazení míry v Lebesgueově integrálu:

,

kde je nějaká Borelova funkce, která je integrovatelná s ohledem na míru pravděpodobnosti.

Disperze, druhy a vlastnosti disperze Pojem disperze

Rozptyl ve statistice se nachází jako směrodatná odchylka jednotlivých hodnot charakteristiky na druhou od aritmetického průměru. V závislosti na počátečních datech se určí pomocí jednoduchých a vážených vzorců rozptylu:

1. Jednoduchá variace(pro neseskupená data) se vypočítá pomocí vzorce:

2. Vážený rozptyl (pro řady variací):

kde n je frekvence (opakovatelnost faktoru X)

Příklad hledání rozptylu

Tato stránka popisuje standardní příklad hledání odchylky, můžete se také podívat na další problémy pro její nalezení

Příklad 1. Určení skupinového, skupinového průměru, meziskupinového a celkového rozptylu

Příklad 2. Nalezení rozptylu a variačního koeficientu v seskupovací tabulce

Příklad 3. Zjištění rozptylu v diskrétní série

Příklad 4. Následující data jsou k dispozici pro skupinu 20 korespondenčních studentů. Je nutné sestrojit intervalovou řadu rozložení charakteristiky, vypočítat průměrnou hodnotu charakteristiky a studovat její rozptyl

Vytvořme intervalové seskupení. Určíme rozsah intervalu pomocí vzorce:

kde X max je maximální hodnota seskupovací charakteristiky; X min – minimální hodnota seskupovací charakteristiky; n – počet intervalů:

Přijímáme n=5. Krok je: h = (192 - 159)/5 = 6,6

Vytvořme intervalové seskupení

Pro další výpočty sestavíme pomocnou tabulku:

X"i – střed intervalu. (například střed intervalu 159 – 165,6 = 162,3)

Průměrnou výšku studentů určíme pomocí vzorce váženého aritmetického průměru:

Pojďme určit rozptyl pomocí vzorce:

Vzorec lze transformovat takto:

Z tohoto vzorce to vyplývá rozptyl se rovná rozdíl mezi průměrem druhých mocnin možností a druhou mocninou a průměrem.

Rozptyl v variační série S ve stejných intervalech metodou momentů lze vypočítat následujícím způsobem pomocí druhé vlastnosti disperze (dělení všech možností hodnotou intervalu). Stanovení rozptylu, počítáno pomocí metody momentů, pomocí následujícího vzorce je méně pracné:

kde i je hodnota intervalu; A je konvenční nula, pro kterou je vhodné použít střed intervalu s nejvyšší frekvencí; m1 je druhá mocnina momentu prvního řádu; m2 - okamžik druhého řádu

Alternativní rozptyl vlastností (pokud se ve statistické populaci charakteristika změní tak, že existují pouze dvě vzájemně se vylučující možnosti, pak se taková variabilita nazývá alternativní) lze vypočítat pomocí vzorce:

Dosazením q = 1- p do tohoto vzorce disperze dostaneme:

Typy rozptylu

Celkový rozptyl měří variace charakteristiky v celé populaci jako celku pod vlivem všech faktorů, které tuto variaci způsobují. Je rovna střední čtverci odchylek jednotlivých hodnot charakteristiky x od celkové střední hodnoty x a lze ji definovat jako jednoduchý rozptyl nebo vážený rozptyl.

Rozptyl v rámci skupiny charakterizuje náhodné variace, tzn. část variace, která je způsobena vlivem nezapočtených faktorů a nezávisí na faktoru-atributu, který tvoří základ skupiny. Taková disperze se rovná střední čtverci odchylek jednotlivých hodnot atributu ve skupině X od aritmetického průměru skupiny a lze ji vypočítat jako jednoduchou disperzi nebo jako váženou disperzi.

Tedy, měření rozptylu v rámci skupiny variace vlastnosti v rámci skupiny a je určena vzorcem:

kde xi je průměr skupiny; ni je počet jednotek ve skupině.

Například rozdíly v rámci skupiny, které je třeba určit v problému studia vlivu kvalifikace pracovníků na úroveň produktivity práce v dílně, vykazují odchylky ve výstupu v každé skupině způsobené všemi možnými faktory ( technický stav vybavení, dostupnost nástrojů a materiálů, věk pracovníků, náročnost na práci atd.), kromě rozdílů v kvalifikační kategorii (v rámci skupiny mají všichni pracovníci stejnou kvalifikaci).

Průměr variací v rámci skupiny odráží náhodnou variaci, tj. tu část variace, která se objevila pod vlivem všech ostatních faktorů, s výjimkou faktoru seskupení. Vypočítá se pomocí vzorce:

Meziskupinová odchylka charakterizuje systematickou variaci výsledné charakteristiky, která je způsobena vlivem faktoru-znaku, který tvoří základ skupiny. Je rovna střední čtverci odchylek skupinových průměrů od celkového průměru. Meziskupinový rozptyl se vypočítá pomocí vzorce:

Tato stránka popisuje standardní příklad hledání odchylky, můžete se také podívat na další problémy pro její nalezení

Příklad 1. Určení skupinového, skupinového průměru, meziskupinového a celkového rozptylu

Příklad 2. Nalezení rozptylu a variačního koeficientu v seskupovací tabulce

Příklad 3. Hledání rozptylu v diskrétní řadě

Příklad 4. Následující data jsou k dispozici pro skupinu 20 korespondenčních studentů. Je nutné sestrojit intervalovou řadu rozložení charakteristiky, vypočítat průměrnou hodnotu charakteristiky a studovat její rozptyl

Vytvořme intervalové seskupení. Určíme rozsah intervalu pomocí vzorce:

kde X max je maximální hodnota seskupovací charakteristiky;
X min – minimální hodnota seskupovací charakteristiky;
n – počet intervalů:

Přijímáme n=5. Krok je: h = (192 - 159)/5 = 6,6

Vytvořme intervalové seskupení

Pro další výpočty sestavíme pomocnou tabulku:

X"i – střed intervalu. (například střed intervalu 159 – 165,6 = 162,3)

Průměrnou výšku studentů určíme pomocí vzorce váženého aritmetického průměru:

Pojďme určit rozptyl pomocí vzorce:

Vzorec lze transformovat takto:

Z tohoto vzorce to vyplývá rozptyl se rovná rozdíl mezi průměrem druhých mocnin možností a druhou mocninou a průměrem.

Rozptyl ve variačních řadách se stejnými intervaly pomocí metody momentů lze vypočítat následujícím způsobem pomocí druhé vlastnosti disperze (dělení všech možností hodnotou intervalu). Stanovení rozptylu, počítáno pomocí metody momentů, pomocí následujícího vzorce je méně pracné:

kde i je hodnota intervalu;
A je konvenční nula, pro kterou je vhodné použít střed intervalu s nejvyšší frekvencí;
m1 je druhá mocnina momentu prvního řádu;
m2 - okamžik druhého řádu

Alternativní rozptyl vlastností (pokud se ve statistické populaci charakteristika změní tak, že existují pouze dvě vzájemně se vylučující možnosti, pak se taková variabilita nazývá alternativní) lze vypočítat pomocí vzorce:

Dosazením q = 1- p do tohoto vzorce disperze dostaneme:

Typy rozptylu

Celkový rozptyl měří variace charakteristiky v celé populaci jako celku pod vlivem všech faktorů, které tuto variaci způsobují. Je rovna střední čtverci odchylek jednotlivých hodnot charakteristiky x od celkové střední hodnoty x a lze ji definovat jako jednoduchý rozptyl nebo vážený rozptyl.

Rozptyl v rámci skupiny charakterizuje náhodnou variaci, tzn. část variace, která je způsobena vlivem nezapočtených faktorů a nezávisí na faktoru-atributu, který tvoří základ skupiny. Taková disperze se rovná střední čtverci odchylek jednotlivých hodnot atributu ve skupině X od aritmetického průměru skupiny a lze ji vypočítat jako jednoduchou disperzi nebo jako váženou disperzi.

Tedy, měření rozptylu v rámci skupiny variace vlastnosti v rámci skupiny a je určena vzorcem:

kde xi je průměr skupiny;
ni je počet jednotek ve skupině.

Například vnitroskupinové odchylky, které je třeba určit v úkolu studovat vliv kvalifikace pracovníků na úroveň produktivity práce v dílně, vykazují odchylky ve výkonu v každé skupině způsobené všemi možnými faktory (technický stav zařízení, dostupnost nářadí a materiály, věk pracovníků, náročnost na práci atd., s výjimkou rozdílů v kvalifikační kategorii (v rámci skupiny mají všichni pracovníci stejnou kvalifikaci).

Pojďme počítat vPANÍVYNIKATrozptyl a směrodatná odchylka vzorky. Pojďme také vypočítat rozptyl náhodná veličina, pokud je známo jeho rozdělení.

Nejprve uvažujme disperze, pak směrodatná odchylka.

Ukázkový rozptyl

Ukázkový rozptyl (vzorový rozptyl,ochutnatrozptyl) charakterizuje rozložení hodnot v poli vzhledem k .

Všechny 3 vzorce jsou matematicky ekvivalentní.

Z prvního vzorce je jasné, že rozptyl vzorku je součet čtverců odchylek každé hodnoty v poli z průměru, děleno velikostí vzorku mínus 1.

odchylky vzorky je použita funkce DISP(), angl. název VAR, tzn. VARiance. Od verze MS EXCEL 2010 je doporučeno používat jeho analogový DISP.V(), anglicky. název VARS, tzn. Ukázka VARiance. Od verze MS EXCEL 2010 je navíc k dispozici funkce DISP.Г(), anglicky. název VARP, tzn. Populační VARiance, která vypočítává disperze Pro populace . Celý rozdíl spočívá ve jmenovateli: místo n-1 jako DISP.V() má DISP.G() ve jmenovateli právě n. Před MS EXCEL 2010 byla k výpočtu rozptylu základního souboru použita funkce VAR().

Ukázkový rozptyl
=QUADROTCL(vzorek)/(POCET(vzorek)-1)
=(SOUČET(Ukázka)-POČET(Ukázka)*PRŮMĚR (Ukázka)^2)/ (POČET (Vzorek)-1)– obvyklý vzorec
=SUM((Vzorek -PRŮMĚR(Ukázka))^2)/ (POČET(Vzor)-1) –

Ukázkový rozptyl se rovná 0, pouze pokud jsou všechny hodnoty navzájem stejné, a tedy rovny průměrná hodnota. Obvykle tím větší hodnota odchylky, tím větší je rozptyl hodnot v poli.

Ukázkový rozptyl je bodový odhad odchylky rozdělení náhodné veličiny, ze které byla vytvořena ochutnat. O stavbě intervaly spolehlivosti při posuzování odchylky si můžete přečíst v článku.

Rozptyl náhodné veličiny

K výpočtu disperze náhodná veličina, musíte ji znát.

Pro odchylky náhodná proměnná X se často označuje Var(X). Disperze rovná se druhé mocnině odchylky od průměru E(X): Var(X)=E[(X-E(X)) 2 ]

disperze vypočítá se podle vzorce:

kde x i je hodnota, kterou může mít náhodná proměnná, a μ je průměrná hodnota (), p(x) je pravděpodobnost, že náhodná proměnná nabude hodnoty x.

Pokud má náhodná proměnná , pak disperze vypočítá se podle vzorce:

Dimenze odchylky odpovídá druhé mocnině měrné jednotky původních hodnot. Pokud například hodnoty ve vzorku představují měření hmotnosti dílu (v kg), pak by rozměr rozptylu byl kg 2 . To může být obtížné interpretovat, takže pro charakterizaci šíření hodnot je to hodnota rovna odmocnina z odchylky – směrodatná odchylka.

Některé vlastnosti odchylky:

Var(X+a)=Var(X), kde X je náhodná proměnná a a je konstanta.

Var(aХ)=a 2 Var(X)

Var(X)=E[(X-E(X)) 2 ]=E=E(X 2)-E(2*X*E(X))+(E(X)) 2 =E(X 2)- 2*E(X)*E(X)+(E(X))2 =E(X2)-(E(X))2

Tato disperzní vlastnost se využívá v článek o lineární regresi.

Var(X+Y)=Var(X) + Var(Y) + 2*Cov(X;Y), kde X a Y jsou náhodné proměnné, Cov(X;Y) je kovariance těchto náhodných proměnných.

Pokud jsou náhodné proměnné nezávislé, pak jsou kovariance se rovná 0, a proto Var(X+Y)=Var(X)+Var(Y). Tato vlastnost disperze se využívá při derivaci.

Ukažme, že pro nezávislé veličiny Var(X-Y)=Var(X+Y). Opravdu, Var(X-Y)= Var(X-Y)= Var(X+(-Y))= Var(X)+Var(-Y)= Var(X)+Var(-Y)= Var( X)+(- 1) 2 Var(Y)= Var(X)+Var(Y)= Var(X+Y). Tato vlastnost disperze se používá ke konstrukci .

Vzorová směrodatná odchylka

Vzorová směrodatná odchylka je mírou toho, jak široce rozptýlené jsou hodnoty ve vzorku vzhledem k jejich .

podle definice směrodatná odchylka rovná se druhé odmocnině z odchylky:

Standardní odchylka nebere v úvahu velikost hodnot v ochutnat, ale pouze stupeň rozptylu hodnot kolem nich průměrný. Abychom to ilustrovali, uveďme příklad.

Vypočítejme směrodatnou odchylku pro 2 vzorky: (1; 5; 9) a (1001; 1005; 1009). V obou případech s=4. Je zřejmé, že poměr směrodatné odchylky k hodnotám pole se mezi vzorky výrazně liší. Pro takové případy se používá Variační koeficient(Variační koeficient, CV) - poměr Standardní odchylka k průměru aritmetický, vyjádřeno v procentech.

V MS EXCEL 2007 a starších verzích pro výpočet Vzorová směrodatná odchylka je použita funkce =STDEVAL(), angl. název STDEV, tzn. Standardní odchylka. Od verze MS EXCEL 2010 se doporučuje používat jeho analog =STANDDEV.B() , angličtina. název STDEV.S, tzn. Ukázka standardní odchylky.

Navíc od verze MS EXCEL 2010 existuje funkce STANDARDEV.G(), angličtina. název STDEV.P, tzn. Standardní odchylka populace, která počítá směrodatná odchylka Pro populace. Celý rozdíl spočívá ve jmenovateli: místo n-1 jako v STANDARDEV.V() má STANDARDEVAL.G() ve jmenovateli právě n.

Standardní odchylka lze také vypočítat přímo pomocí níže uvedených vzorců (viz soubor s příkladem)
=ROOT(QUADROTCL(Ukázka)/(POČET(Ukázka)-1))
=KOŘEN((SOUČET(Ukázka)-POČET(Ukázka)*PRŮMĚR (Ukázka)^2)/(POČET (Vzorek)-1))

Další míry rozptylu

Funkce SQUADROTCL() počítá s součet čtverců odchylek hodnot od jejich průměrný. Tato funkce vrátí stejný výsledek jako vzorec =DISP.G( Ochutnat)*KONTROLA( Ochutnat), kde Ochutnat- odkaz na rozsah obsahující pole vzorových hodnot (). Výpočty ve funkci QUADROCL() se provádějí podle vzorce:

Funkce SROTCL() je také mírou šíření datové sady. Funkce SROTCL() vypočítá průměr absolutních hodnot odchylek hodnot od průměrný. Tato funkce vrátí stejný výsledek jako vzorec =SOUČETNÍ PRODUKT(ABS(Vzorek-PRŮMĚR (Ukázka)))/POČET (Vzorek), Kde Ochutnat- odkaz na rozsah obsahující pole vzorových hodnot.

Výpočty ve funkci SROTCL () se provádějí podle vzorce:

Podle výběrového šetření byli vkladatelé seskupeni podle velikosti jejich vkladu v městské Sberbank:

Definovat:

1) rozsah variace;

2) průměrná velikost vkladu;

3) průměrná lineární odchylka;

4) disperze;

5) směrodatná odchylka;

6) variační koeficient příspěvků.

Řešení:

Tato distribuční řada obsahuje otevřené intervaly. V takové řadě se běžně předpokládá, že hodnota intervalu první skupiny je rovna hodnotě intervalu další skupiny a hodnota intervalu poslední skupiny je rovna hodnotě intervalu předchozí.

Hodnota intervalu druhé skupiny je rovna 200, tedy hodnota první skupiny je také rovna 200. Hodnota intervalu předposlední skupiny je rovna 200, což znamená, že i poslední interval bude mají hodnotu 200.

1) Definujme variační rozsah jako rozdíl mezi největší a nejnižší hodnota znamení:

Rozsah variací ve velikosti vkladu je 1 000 rublů.

2) Průměrná výše příspěvku bude stanovena pomocí vzorce váženého aritmetického průměru.

Pojďme nejprve určit diskrétní množství funkce v každém intervalu. Abychom to udělali, pomocí jednoduchého vzorce aritmetického průměru najdeme středy intervalů.

Průměrná hodnota prvního intervalu bude:

druhý - 500 atd.

Výsledky výpočtu zapišme do tabulky:

Částka vkladu, rub.	Počet vkladatelů, f	Střed intervalu, x	xf
200-400	32	300	9600
400-600	56	500	28000
600-800	120	700	84000
800-1000	104	900	93600
1000-1200	88	1100	96800
Celkový	400	-	312000

Průměrný vklad v městské Sberbank bude 780 rublů:

3) Průměrná lineární odchylka je aritmetický průměr absolutních odchylek jednotlivých hodnot charakteristiky od celkového průměru:

Postup výpočtu průměrné lineární odchylky v řadě intervalového rozdělení je následující:

1. Vypočte se vážený aritmetický průměr, jak je uvedeno v odstavci 2).

2. Stanoví se absolutní odchylky od průměru:

3. Výsledné odchylky se násobí frekvencemi:

4. Najděte součet vážených odchylek bez zohlednění znaménka:

5. Součet vážených odchylek se vydělí součtem četností:

Je vhodné použít tabulku dat výpočtu:

Částka vkladu, rub.	Počet vkladatelů, f	Střed intervalu, x
200-400	32	300	-480	480	15360
400-600	56	500	-280	280	15680
600-800	120	700	-80	80	9600
800-1000	104	900	120	120	12480
1000-1200	88	1100	320	320	28160
Celkový	400	-	-	-	81280

Průměrná lineární odchylka velikosti vkladu klientů Sberbank je 203,2 rublů.

4) Disperze je aritmetický průměr druhých mocnin odchylek každé hodnoty atributu od aritmetického průměru.

Výpočet rozptylu v intervalové řádky distribuce se provádí podle vzorce:

Postup pro výpočet rozptylu je v tomto případě následující:

1. Určete vážený aritmetický průměr, jak je uvedeno v odstavci 2).

2. Najděte odchylky od průměru:

3. Druhá mocnina odchylky každé možnosti od průměru:

4. Vynásobte druhé mocniny odchylek vahami (frekvencemi):

5. Shrňte výsledné produkty:

6. Výsledná částka se vydělí součtem vah (četností):

Uveďme výpočty do tabulky:

Částka vkladu, rub.	Počet vkladatelů, f	Střed intervalu, x
200-400	32	300	-480	230400	7372800
400-600	56	500	-280	78400	4390400
600-800	120	700	-80	6400	768000
800-1000	104	900	120	14400	1497600
1000-1200	88	1100	320	102400	9011200
Celkový	400	-	-	-	23040000