". První část nastiňuje ustanovení, která jsou minimálně nezbytná pro pochopení chemometrie, a druhá část obsahuje fakta, která potřebujete znát pro hlubší pochopení metod vícerozměrné analýzy. Prezentace je ilustrována příklady vytvořenými v excelovém sešitu Matrix.xls který doprovází tento dokument.

Odkazy na příklady jsou umístěny v textu jako objekty aplikace Excel. Tyto příklady jsou abstraktní povahy, nejsou nijak vázány na úkoly. analytická chemie. Skutečné příklady použití maticové algebry v chemometrii je diskutováno v jiných textech věnovaných různým chemometrickým aplikacím.

Většina měření prováděných v analytické chemii není přímá, ale nepřímý. To znamená, že v experimentu se místo hodnoty požadovaného analytu C (koncentrace) získá jiná hodnota X(signál) související s C, ale ne rovný C, tzn. X(C) ≠ C. Zpravidla typ závislosti X(C) není známo, ale naštěstí v analytické chemii je většina měření proporcionální. To znamená, že jako koncentrace C in A krát se signál X zvýší o stejnou hodnotu, tzn. X(A C) = a x(C). Signály jsou navíc také aditivní, takže signál ze vzorku obsahujícího dvě látky o koncentracích C 1 a C 2 bude roven součtu signálů z každé složky, tzn. X(C1 + C2) = X(C1)+ X(C2). Proporcionalita a aditivnost dohromady dávají linearita. Pro ilustraci principu linearity lze uvést mnoho příkladů, postačí však uvést dva nejvýraznější příklady – chromatografii a spektroskopii. Druhým rysem experimentu v analytické chemii je vícekanálový. Moderní analytická zařízení současně měří signály pro mnoho kanálů. Například intenzita prostupu světla se měří pro více vlnových délek najednou, tzn. rozsah. Proto se v experimentu zabýváme různými signály X 1 , X 2 ,...., X n charakterizující soubor koncentrací C 1 ,C 2, ..., C m látek přítomných ve studovaném systému.

Rýže. 1 Spectra

Analytický experiment je tedy charakterizován linearitou a multidimenzionálností. Proto je vhodné považovat experimentální data za vektory a matice a manipulovat s nimi pomocí aparátu maticové algebry. Plodnost tohoto přístupu ilustruje příklad ukázaný v , který ukazuje tři spektra pro 200 vlnových délek od 4000 do 4796 cm–1. První ( X 1) a druhý ( X 2) spektra byla získána pro standardní vzorky, ve kterých jsou známé koncentrace dvou látek A a B: v prvním vzorku [A] = 0,5, [B] = 0,1 a ve druhém vzorku [A] = 0,2, [ B] = 0,6. Co lze říci o novém, neznámém vzorku, jehož spektrum je naznačeno X 3 ?

Zvažte tři experimentální spektra X 1 , X 2 a X 3 jako tři vektory dimenze 200. Pomocí lineární algebry to lze snadno ukázat X 3 = 0.1 X 1 +0.3 X 2, takže třetí vzorek zjevně obsahuje pouze látky A a B v koncentracích [A] = 0,5×0,1 + 0,2×0,3 = 0,11 a [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Základní informace

1.1 Matice

Matice nazývá se například obdélníková tabulka čísel

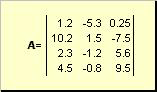
Rýže. 2 Matice

Matice jsou označeny velkými tučnými písmeny ( A), a jejich prvky - s odpovídajícími malými písmeny s indexy, tzn. A ij První index čísluje řádky a druhý číslo sloupce. V chemometrii je obvyklé označovat maximální hodnotu indexu stejným písmenem jako index samotný, ale velkými písmeny. Proto matrice A lze také napsat jako ( A ij , i = 1,..., já; j = 1,..., J). Pro příklad matice já = 4, J= 3 a A 23 = −7.5.

Dvojice čísel já A J se nazývá rozměr matice a označuje se jako já× J. Příkladem matice v chemometrii je soubor spekter získaných pro já vzorky na J vlnové délky.

1.2. Nejjednodušší operace s maticemi

Matice mohou násobit čísly. V tomto případě je každý prvek vynásoben tímto číslem. Například -

Rýže. 3 Násobení matice číslem

Dvě matice stejné dimenze mohou být elementární složit A odčítat. Například,

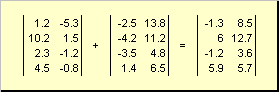
Rýže. 4 Sčítání matice

Násobením číslem a sčítáním se získá matice stejného rozměru.

Nulová matice je matice skládající se z nul. Je určeno Ó. To je zřejmé A+Ó = A, A−A = Ó a 0 A = Ó.

Matrix může přemístit. Při této operaci se matrice překlopí, tzn. řádky a sloupce jsou prohozeny. Transpozice je označena pomlčkou, A“ nebo index A t . Pokud tedy A = {A ij , i = 1,..., já; j = 1,...,J), Že A t = ( A ji , j = 1,...,J; i = 1,..., já). Například

Rýže. 5 Maticová transpozice

Je zřejmé, že ( A t) t = A, (A+B) t = A t+ B t .

1.3. Maticové násobení

Matice mohou násobit, ale pouze pokud mají odpovídající rozměry. Proč tomu tak je, bude zřejmé z definice. Produkt Matrix A, rozměr já× K a matrice B, rozměr K× J, se nazývá matice C, rozměr já× J, jehož prvky jsou čísla

Tedy pro produkt AB je nutné, aby počet sloupců v levé matici A se rovnal počtu řádků v pravé matici B. Příklad produktu Matrix -

Obr.6 Součin matic

Pravidlo násobení matic může být formulováno následovně. Najít prvek matice C stojící na křižovatce i-tý řádek a j-tý sloupec ( C ij) je třeba vynásobit prvek po prvku i-tý řádek první matice A na j-tý sloupec druhé matice B a sečtěte všechny výsledky. Takže v zobrazeném příkladu je prvek ze třetího řádku a druhého sloupce získán jako součet prvků ve třetím řádku A a druhý sloupec B

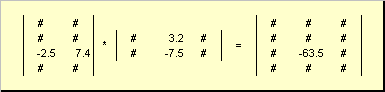
Obr.7 Prvek součinu matic

Součin matric závisí na pořadí, tzn. AB ≠ BA, alespoň z rozměrových důvodů. Říká se, že je nekomutativní. Součin matic je však asociativní. Znamená to, že ABC = (AB)C = A(před naším letopočtem). Navíc je také distributivní, tzn. A(B+C) = AB+AC. To je zřejmé AO = Ó.

1.4. Čtvercové matice

Pokud se počet sloupců matice rovná počtu jejích řádků ( já = J=N), pak se taková matice nazývá čtverec. V této části se budeme zabývat pouze těmito maticemi. Mezi těmito maticemi lze vyčlenit matice se speciálními vlastnostmi.

Osamělý matice (označená já a někdy E) je matice, ve které jsou všechny prvky rovny nule, kromě těch diagonálních, které se rovnají 1, tzn.

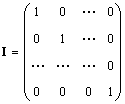
Očividně AI = IA = A.

Matice se nazývá úhlopříčka, pokud všechny jeho prvky, kromě těch diagonálních ( A ii) se rovnají nule. Například

Rýže. 8 Diagonální matice

Matice A nazvaný vrchol trojúhelníkový, jsou-li všechny její prvky ležící pod úhlopříčkou rovny nule, tzn. A ij= 0, při i>j. Například

Rýže. 9 Horní trojúhelníková matice

Spodní trojúhelníková matice je definována podobně.

Matice A volal symetrický, Pokud A t = A. Jinými slovy A ij = A ji. Například

Rýže. 10 Symetrická matice

Matice A volal ortogonální, Pokud

A t A = AA t = já.

Matice se nazývá normální Li

1.5. Stopa a determinant

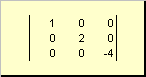
Následujícíčtvercová matice A(označeno Tr( A) nebo Sp( A)) je součet jejích diagonálních prvků,

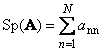
Například,

Rýže. 11 Maticová stopa

To je zřejmé

Sp(a A) = α Sp( A) A

Sp( A+B) = Sp( A)+ Sp( B).

Dá se to ukázat

Sp( A) = Sp( A t), Sp( já) = N,

a také to

Sp( AB) = Sp( BA).

Další důležitou vlastností čtvercové matice je její determinant(označeno det( A)). Definice determinantu v obecný případ poměrně komplikované, takže začneme tou nejjednodušší možností – maticí A rozměr (2×2). Pak

Pro matici (3×3) bude determinant roven

V případě matice ( N× N) determinant se vypočítá jako součet 1 2 3 ... N= N! termíny, z nichž každý je roven

Indexy k 1 , k 2 ,..., k N jsou definovány jako všechny možné uspořádané permutace rčísla v sadě (1, 2, ... , N). Výpočet maticového determinantu je složitý postup, který se v praxi provádí pomocí speciálních programů. Například,

Rýže. 12 Maticový determinant

Zaznamenáváme pouze zřejmé vlastnosti:

det( já) = 1, det( A) = det( A t),

det( AB) = det( A)det( B).

1.6. vektory

Pokud má matice pouze jeden sloupec ( J= 1), pak se takový objekt nazývá vektor. Přesněji sloupcový vektor. Například

Za matice skládající se z jedné řady lze také považovat kupř

Tento objekt je také vektor, ale řádkový vektor. Při analýze dat je důležité pochopit, se kterými vektory máme co do činění - sloupci nebo řádky. Takže spektrum odebrané pro jeden vzorek lze považovat za řádkový vektor. Potom by se soubor spektrálních intenzit při určité vlnové délce pro všechny vzorky měl považovat za sloupcový vektor.

Rozměr vektoru je počet jeho prvků.

Je jasné, že libovolný sloupcový vektor lze transpozicí transformovat na vektor řádkový, tzn.

V těch případech, kdy není specificky specifikována forma vektoru, ale je jednoduše řečeno vektor, pak znamenají sloupcový vektor. Tohoto pravidla se budeme také držet. Vektor je označen malým přímým tučným písmenem. Nulový vektor je vektor, jehož všechny prvky jsou rovny nule. Označuje se 0 .

1.7. Nejjednodušší operace s vektory

Vektory lze sčítat a násobit čísly stejným způsobem jako matice. Například,

Rýže. 13 Operace s vektory

Dva vektory X A y volal kolineární, pokud existuje číslo α takové, že

1.8. Součin vektorů

Dva vektory stejné dimenze N lze násobit. Nechť jsou dva vektory X = (X 1 , X 2 ,...,X N) t a y = (y 1 , y 2 ,...,y N) t. Podle pravidla násobení „řádek po sloupci“ z nich můžeme vytvořit dva produkty: X t y A xy t . První práce

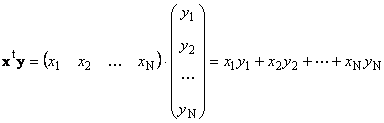
volal skalární nebo vnitřní. Jeho výsledkem je číslo. Používá také notaci ( X,y)= X t y. Například,

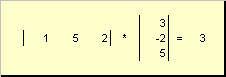
Rýže. 14 Vnitřní (skalární) součin

Druhá práce

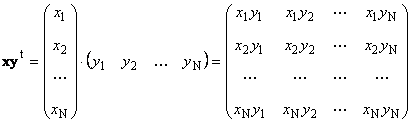
volal externí. Jeho výsledkem je matice rozměrů ( N× N). Například,

Rýže. 15 Vnější produkt

Volají se vektory, jejichž skalární součin je roven nule ortogonální.

1.9. Vektorová norma

Skalární součin vektoru se sebou samým se nazývá skalární čtverec. Tato hodnota

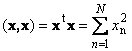
definuje čtverec délka vektor X. K označení délky (také nazývané norma vektor) se používá zápis

Například,

Rýže. 16 Vektorová norma

Vektor jednotkové délky (|| X|| = 1) se nazývá normalizovaný. Nenulový vektor ( X ≠ 0 ) lze normalizovat dělením délkou, tzn. X = ||X|| (X/||X||) = ||X|| E. Tady E = X/||X|| je normalizovaný vektor.

Vektory se nazývají ortonormální, pokud jsou všechny normalizované a párově ortogonální.

1.10. Úhel mezi vektory

Skalární součin definuje a rohφ mezi dvěma vektory X A y

Pokud jsou vektory ortogonální, pak cosφ = 0 a φ = π/2, a pokud jsou kolineární, pak cosφ = 1 a φ = 0.

1.11. Vektorové znázornění matice

Každá matrice A velikost já× J může být reprezentován jako soubor vektorů

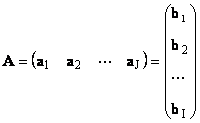
Zde každý vektor A j je j-tý sloupec a řádek vektor b i je i-tý řádek matice A

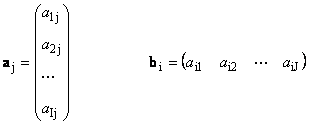
1.12. Lineárně závislé vektory

vektory stejné dimenze ( N) lze sčítat a násobit číslem, stejně jako matice. Výsledkem je vektor stejné dimenze. Nechť existuje několik vektorů stejné dimenze X 1 , X 2 ,...,X K a stejný počet čísel α α 1 , α 2 ,...,α K. Vektor

y= α 1 X 1 + α 2 X 2 +...+α K X K

volal lineární kombinace vektory X k .

Pokud existují taková nenulová čísla α k ≠ 0, k = 1,..., K, Co y = 0 , pak taková množina vektorů X k volal lineárně závislé. Jinak se vektory nazývají lineárně nezávislé. Například vektory X 1 = (2, 2) ta X 2 = (−1, −1) t jsou lineárně závislé, protože X 1 +2X 2 = 0

1.13. Hodnost matice

Zvažte sadu K vektory X 1 , X 2 ,...,X K rozměry N. Hodnost tohoto systému vektorů je maximální počet lineárně nezávislých vektorů. Například v sadě

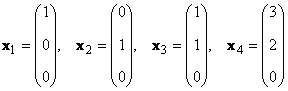
existují například pouze dva lineárně nezávislé vektory X 1 a X 2, takže jeho pořadí je 2.

Je zřejmé, že pokud je v sadě více vektorů, než je jejich rozměr ( K>N), pak jsou nutně lineárně závislé.

Hodnost matice(označeno hodností ( A)) je hodnost systému vektorů, ze kterých se skládá. Ačkoli může být jakákoli matice reprezentována dvěma způsoby (sloupcové vektory nebo řádkové vektory), nemá to vliv na hodnotu pořadí, protože

1.14. inverzní matice

čtvercová matice A se nazývá nedegenerovaný, pokud má jedinečný zvrátit matice A-1 , určeno podmínkami

AA −1 = A −1 A = já.

Inverzní matice neexistuje pro všechny matice. Nezbytnou a postačující podmínkou pro nedegeneraci je

det( A) ≠ 0 nebo pořadí ( A) = N.

Maticová inverze je složitá procedura, pro kterou existují speciální programy. Například,

Rýže. 17 Inverze matice

Dáme vzorce pro nejjednodušší případ - matice 2 × 2

Pokud matrice A A B jsou tedy nedegenerované

(AB) −1 = B −1 A −1 .

1.15. Pseudoinverzní matice

Pokud matice A je degenerovaný a inverzní matice neexistuje, pak v některých případech lze použít pseudoinverzní matice, která je jako taková matice definována A+ to

AA + A = A.

Pseudoinverzní matice není jediná a její podoba závisí na konstrukční metodě. Například pro obdélníkovou matici můžete použít metodu Moore-Penrose.

Pokud je počet sloupců menší než počet řádků, pak

A + =(A t A) −1 A t

Například,

Rýže. 17a Pseudomaticová inverze

Pokud je počet sloupců větší než počet řádků, pak

A + =A t ( AA t) −1

1.16. Násobení vektoru maticí

Vektor X lze vynásobit maticí A vhodný rozměr. V tomto případě se sloupcový vektor násobí vpravo Sekera a vektorový řetězec je vlevo X t A. Pokud je rozměr vektoru J a rozměr matice já× J pak je výsledkem vektor dimenze já. Například,

Rýže. 18 Násobení vektorové matice

Pokud matice A- náměstí ( já× já), pak vektor y = Sekera má stejný rozměr jako X. To je zřejmé

A(α 1 X 1 + α 2 X 2) = a 1 Sekera 1 + α 2 Sekera 2 .

Proto lze matice považovat za lineární transformace vektorů. Zejména X = X, Vůl = 0 .

2. Další informace

2.1. Soustavy lineárních rovnic

Nechat A- velikost matrice já× J, A b- rozměrový vektor J. Zvažte rovnici

Sekera = b

vzhledem k vektoru X, rozměry já. V podstatě se jedná o systém já lineární rovnice S J neznámý X 1 ,...,X J. Řešení existuje tehdy a jen tehdy

hodnost( A) = hodnost ( B) = R,

Kde B je rozšířená matice rozměrů já×( J+1) sestávající z matice A, polstrovaný sloupkem b, B = (A b). Jinak jsou rovnice nekonzistentní.

Li R = já = J, pak je řešení jedinečné

X = A −1 b.

Li R < já, pak existuje mnoho různých řešení, která lze vyjádřit pomocí lineární kombinace J−R vektory. Systém homogenní rovnice Sekera = 0 se čtvercovou maticí A (N× N) má netriviální řešení ( X ≠ 0 ) tehdy a jen tehdy, když det( A) = 0. Pokud R= hodnost( A)<N, pak tam jsou N−R lineárně nezávislá řešení.

2.2. Bilineární a kvadratické formy

Li A je čtvercová matice a X A y- vektory odpovídající dimenze, pak skalární součin tvaru X t Ano volal bilineární tvar definovaný maticí A. Na X = y výraz X t Sekera volal kvadratický formulář.

2.3. Pozitivně určité matice

čtvercová matice A volal pozitivní definitivní, pokud pro jakýkoli nenulový vektor X ≠ 0 ,

X t Sekera > 0.

The negativní (X t Sekera < 0), nezáporné (X t Sekera≥ 0) a nepozitivní (X t Sekera≤ 0) určité matice.

2.4. Choleský rozklad

Pokud je symetrická matice A je pozitivně definitní, pak existuje jedinečná trojúhelníková matice U s pozitivními prvky, pro které

A = U t U.

Například,

Rýže. 19 Choleský rozklad

2.5. polární rozklad

Nechat A je nedegenerovaná čtvercová matice rozměrů N× N. Pak je tu unikát polární výkon

A = SR,

Kde S je nezáporná symetrická matice a R je ortogonální matice. matrice S A R lze explicitně definovat:

S 2 = AA t nebo S = (AA t) ½ a R = S −1 A = (AA t) -½ A.

Například,

Rýže. 20 Polární rozklad

Pokud matice A je degenerovaný, pak rozklad není jedinečný - jmenovitě: S stále sám, ale R může jich být mnoho. Polární rozklad představuje matici A jako kombinace komprese/natažení S a soustružení R.

2.6. Vlastní vektory a vlastní čísla

Nechat A je čtvercová matice. Vektor proti volal vlastní vektor matrice A, Pokud

Av = λ proti,

kde se nazývá číslo λ vlastní hodnota matrice A. Tedy transformace, kterou matice provádí A přes vektor proti, je redukován na jednoduché natažení nebo stlačení s faktorem λ. Vlastní vektor je určen až do násobení konstantou α ≠ 0, tzn. Li proti je vlastní vektor, pak α proti je také vlastním vektorem.

2.7. Vlastní čísla

Na matrice A, rozměr ( N× N) nemůže být větší než N vlastní čísla. uspokojují charakteristická rovnice

det( A − λ já) = 0,

bytost algebraická rovnice N-tý řád. Zejména pro matici 2×2 má charakteristická rovnice tvar

Například,

Rýže. 21 Vlastní čísla

Množina vlastních čísel λ 1 ,..., λ N matrice A volal spektrum A.

Spektrum má různé vlastnosti. Zejména

det( A) = λ 1×...×λ N, Sp( A) = λi +...+λ N.

Vlastními hodnotami libovolné matice mohou být komplexní čísla, ale pokud je matice symetrická ( A t = A), pak jsou jeho vlastní hodnoty skutečné.

2.8. Vlastní vektory

Na matrice A, rozměr ( N× N) nemůže být větší než N vlastní vektory, z nichž každý odpovídá své vlastní hodnotě. K určení vlastního vektoru proti n potřebujete vyřešit soustavu homogenních rovnic

(A − λ n já)proti n = 0 .

Má to netriviální řešení, protože det( A-λ n já) = 0.

Například,

Rýže. 22 Vlastní vektory

Vlastní vektory symetrické matice jsou ortogonální.

Vlastní vektor čtvercové matice je ten, který po vynásobení danou maticí vede ke kolineárnímu vektoru. Jednoduše řečeno, když je matice vynásobena vlastním vektorem, druhý zůstává stejný, ale vynásobený nějakým číslem.

Definice

Vlastní vektor je nenulový vektor V, který se po vynásobení čtvercovou maticí M stane sám sebou zvětšeným o nějaké číslo λ. V algebraickém zápisu to vypadá takto:

M × V = λ × V,

kde λ je vlastní číslo matice M.

Uvažujme číselný příklad. Pro usnadnění psaní budou čísla v matici oddělena středníkem. Řekněme, že máme matici:

• M = 0; 4;
• 6; 10.

Vynásobme to sloupcovým vektorem:

• V = -2;

Při vynásobení matice sloupcovým vektorem dostaneme také sloupcový vektor. V přísném matematickém jazyce by vzorec pro násobení matice 2 × 2 sloupcovým vektorem vypadal takto:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 znamená prvek matice M, stojící v prvním řádku a prvním sloupci, a M22 je prvek umístěný v druhém řádku a druhém sloupci. Pro naši matici jsou tyto prvky M11 = 0, M12 = 4, M21 = 6, M22 10. Pro sloupcový vektor jsou tyto hodnoty V11 = –2, V21 = 1. Podle tohoto vzorce dostaneme následující výsledek součinu čtvercové matice vektorem:

• M x V = 0 x (-2) + (4) x (1) = 4;
• 6 x (-2) + 10 x (1) = -2.

Pro usnadnění zapíšeme sloupcový vektor do řádku. Čtvercovou matici jsme tedy vynásobili vektorem (-2; 1), výsledkem je vektor (4; -2). Je zřejmé, že se jedná o stejný vektor vynásobený λ = -2. Lambda v tomto případě označuje vlastní hodnotu matice.

Vlastní vektor matice je kolineární vektor, to znamená objekt, který nemění svou polohu v prostoru, když je vynásoben maticí. Pojem kolinearity ve vektorové algebře je podobný termínu rovnoběžnosti v geometrii. V geometrické interpretaci jsou kolineární vektory rovnoběžné směrované segmenty různých délek. Od dob Euklida víme, že jedna přímka má nekonečný počet přímek rovnoběžných s ní, takže je logické předpokládat, že každá matice má nekonečný počet vlastních vektorů.

Z předchozího příkladu je vidět, že jak (-8; 4), tak (16; -8) a (32, -16) mohou být vlastní vektory. To vše jsou kolineární vektory odpovídající vlastní hodnotě λ = -2. Při vynásobení původní matice těmito vektory dostaneme ve výsledku stále vektor, který se od originálu liší 2x. Proto je při řešení úloh pro nalezení vlastního vektoru požadováno najít pouze lineárně nezávislé vektorové objekty. Nejčastěji pro matici n × n existuje n-tý počet vlastních vektorů. Naše kalkulačka je navržena pro analýzu čtvercových matic druhého řádu, takže ve výsledku budou téměř vždy nalezeny dva vlastní vektory, kromě případů, kdy se shodují.

Ve výše uvedeném příkladu jsme předem znali vlastní vektor původní matice a vizuálně jsme určili číslo lambda. V praxi se však vše děje naopak: na začátku jsou vlastní čísla a teprve potom vlastní vektory.

Algoritmus řešení

Podívejme se znovu na původní matici M a zkusme najít oba její vlastní vektory. Matice tedy vypadá takto:

• M = 0; 4;
• 6; 10.

Nejprve musíme určit vlastní hodnotu λ, pro kterou musíme vypočítat determinant následující matice:

• (0 - λ); 4;
• 6; (10 - λ).

Tato matrice získáme odečtením neznámé λ od prvků na hlavní diagonále. Determinant je určen standardním vzorcem:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Protože náš vektor nesmí být nulový, vezmeme výslednou rovnici jako lineárně závislou a srovnáme náš determinant detA s nulou.

(0 − λ) × (10 − λ) − 24 = 0

Otevřeme závorky a získáme charakteristickou rovnici matice:

λ 2 − 10λ − 24 = 0

To je standardní kvadratická rovnice, který má být řešen z hlediska diskriminačního.

D \u003d b 2 – 4ac \u003d (-10) × 2 – 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Kořen diskriminantu je sqrt(D) = 14, takže λ1 = -2, λ2 = 12. Nyní pro každou hodnotu lambda potřebujeme najít vlastní vektor. Vyjádřeme koeficienty soustavy pro λ = -2.

• M − λ × E = 2; 4;
• 6; 12.

V tomto vzorci je E matice identity. Na základě získané matice sestavíme soustavu lineárních rovnic:

2x + 4 roky = 6x + 12 let

kde x a y jsou prvky vlastního vektoru.

Sesbírejme všechna X nalevo a všechna Y napravo. Pochopitelně - 4x = 8 let. Vydělte výraz číslem -4 a dostanete x = -2y. Nyní můžeme určit první vlastní vektor matice tím, že vezmeme libovolné hodnoty neznámých (pamatujte na nekonečno lineárně závislých vlastních vektorů). Vezměme y = 1, pak x = -2. První vlastní vektor tedy vypadá jako V1 = (–2; 1). Vraťte se na začátek článku. Byl to tento vektorový objekt, kterým jsme vynásobili matici, abychom demonstrovali koncept vlastního vektoru.

Nyní najdeme vlastní vektor pro λ = 12.

• M - X x E = -12; 4
• 6; -2.

Sestavme stejný systém lineárních rovnic;

• -12x + 4y = 6x − 2y
• -18x = -6 let
• 3x=y.

Nyní vezměme x = 1, tedy y = 3. Druhý vlastní vektor tedy vypadá jako V2 = (1; 3). Při vynásobení původní matice tímto vektorem bude výsledkem vždy stejný vektor vynásobený 12. Tím je algoritmus řešení dokončen. Nyní víte, jak ručně definovat vlastní vektor matice.

• determinant;
• stopa, tedy součet prvků na hlavní diagonále;
• pořadí, tj. maximální počet lineárně nezávislých řádků/sloupců.

Program pracuje podle výše uvedeného algoritmu a minimalizuje proces řešení. Je důležité upozornit, že v programu je lambda označena písmenem „c“. Podívejme se na číselný příklad.

Příklad programu

Pokusme se definovat vlastní vektory pro následující matici:

• M = 5; 13;
• 4; 14.

Zadejme tyto hodnoty do buněk kalkulačky a získáme odpověď v následujícím tvaru:

• Pořadí matice: 2;
• Maticový determinant: 18;
• Maticová stopa: 19;
• Výpočet vlastního vektoru: c 2 − 19,00c + 18,00 (charakteristická rovnice);
• Výpočet vlastního vektoru: 18 (první hodnota lambda);
• Výpočet vlastního vektoru: 1 (druhá hodnota lambda);
• Soustava rovnic vektoru 1: -13x1 + 13y1 = 4x1 − 4y1;
• Systém rovnic vektoru 2: 4x1 + 13y1 = 4x1 + 13y1;
• Vlastní vektor 1: (1; 1);
• Vlastní vektor 2: (-3,25; 1).

Tak jsme získali dva lineárně nezávislé vlastní vektory.

Závěr

Lineární algebra a analytická geometrie- standardní předměty pro každého prváka technického zaměření. Velký počet vektorů a matic je děsivá a v tak těžkopádných výpočtech je snadné udělat chybu. Náš program umožní studentům zkontrolovat své výpočty nebo automaticky vyřešit problém s nalezením vlastního vektoru. V našem katalogu jsou další kalkulačky lineární algebry, využijte je při studiu nebo práci.

Definice 9.3. Vektor X volal vlastní vektor matrice A pokud takové číslo existuje λ, že platí rovnost: A X= λ X, tedy výsledek přihlášky do X lineární transformace daná maticí A, je násobení tohoto vektoru číslem λ . Samotné číslo λ volal vlastní číslo matrice A.

Dosazování do vzorců (9.3) x`j = λxj, získáme soustavu rovnic pro určení souřadnic vlastního vektoru:

. (9.5)

Tento lineární homogenní systém bude mít netriviální řešení pouze v případě, že jeho hlavní determinant je 0 (Cramerovo pravidlo). Zapsáním této podmínky do formuláře:

dostaneme rovnici pro určení vlastních hodnot λ volal charakteristická rovnice. Stručně to lze znázornit takto:

| A-λE | = 0, (9.6)

protože jeho levá strana je determinantem matice A-λE. Polynom s ohledem na λ | A-λE| volal charakteristický polynom matrice A.

Vlastnosti charakteristického polynomu:

1) Charakteristický polynom lineární transformace nezávisí na volbě báze. Důkaz. (viz (9.4)), ale proto,. Nezáleží tedy na volbě základu. Proto a | A-λE| se při přechodu na nový základ nemění.

2) Je-li matice A lineární transformace je symetrický(ti. a ij = a ji), pak všechny kořeny charakteristická rovnice(9.6) jsou reálná čísla.

Vlastnosti vlastních čísel a vlastních vektorů:

1) Zvolíme-li základ z vlastních vektorů x 1, x 2, x 3 odpovídající vlastním číslům λ 1, λ 2, λ 3 matrice A, pak v tomto základě má lineární transformace A diagonální matici:

(9.7) Důkaz této vlastnosti vyplývá z definice vlastních vektorů.

2) Pokud vlastní čísla transformace A jsou různé, pak jim odpovídající vlastní vektory jsou lineárně nezávislé.

3) Je-li charakteristický polynom matice A má tři různé kořeny, pak v nějakém základu matice A má diagonální tvar.

Pojďme najít vlastní čísla a vlastní vektory matice Udělejme charakteristickou rovnici: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Najděte souřadnice vlastních vektorů odpovídajících každé nalezené hodnotě λ. Z (9.5) vyplývá, že pokud X (1) ={x 1, x 2, x 3) je vlastní vektor odpovídající λ 1 = -2, tedy

je kolaborativní, ale neurčitý systém. Jeho řešení lze zapsat jako X (1) ={A,0,-A), kde a je libovolné číslo. Zejména pokud to požadujete | X (1) |=1, X (1) =

Nahrazení do systému (9.5) λ 2 =3, dostaneme systém pro určení souřadnic druhého vlastního vektoru - X (2) ={y1, y2, y3}:

, kde X (2) ={b,-b,b) nebo za předpokladu | X (2) |=1, X (2) =

Pro λ 3 = 6 najděte vlastní vektor X (3) ={z1, z2, z3}:

, X (3) ={C,2c,c) nebo v normalizované verzi

x (3) = Je to vidět X (1) X (2) = ab-ab= 0, X (1) X (3) = ac-ac= 0, X (2) X (3) = před naším letopočtem- 2bc + bc= 0. Vlastní vektory této matice jsou tedy párově ortogonální.

Přednáška 10

Kvadratické formy a jejich spojení se symetrickými maticemi. Vlastnosti vlastních vektorů a vlastních hodnot symetrické matice. Redukce kvadratické formy na kanonickou formu.

Definice 10.1.kvadratická forma reálné proměnné x 1, x 2,…, x n nazývá se polynom druhého stupně vzhledem k těmto proměnným, který neobsahuje volný člen a členy prvního stupně.

Příklady kvadratických forem:

(n = 2),

(n = 3). (10.1)

Připomeňme si definici symetrické matice uvedenou v minulé přednášce:

Definice 10.2.Čtvercová matice se nazývá symetrický, if , tedy pokud jsou prvky matice symetrické vzhledem k hlavní diagonále stejné.

Vlastnosti vlastních čísel a vlastních vektorů symetrické matice:

1) Všechny vlastní hodnoty symetrické matice jsou reálné.

Důkaz (pro n = 2).

Nechte matici A vypadá jako: . Udělejme charakteristickou rovnici:

(10.2) Najděte diskriminant:

Rovnice má proto pouze skutečné kořeny.

2) Vlastní vektory symetrické matice jsou ortogonální.

Důkaz (pro n= 2).

Souřadnice vlastních vektorů a musí splňovat rovnice.

Matice diagonálního typu jsou uspořádány nejjednodušeji. Nabízí se otázka, zda je možné najít základ, ve kterém by matice lineárního operátoru měla diagonální tvar. Takový základ existuje.
Nechť je dán lineární prostor R n a v něm působící lineární operátor A; v tomto případě operátor A vezme R n do sebe, tedy A:R n → R n .

Definice. Nenulový vektor se nazývá vlastní vektor operátoru A, pokud se operátor A převede na vektor kolineární k němu, to jest . Číslo λ se nazývá vlastní číslo nebo vlastní číslo operátoru A odpovídající vlastnímu vektoru .
Zaznamenáváme některé vlastnosti vlastních čísel a vlastních vektorů.
1. Libovolná lineární kombinace vlastních vektorů operátoru A odpovídajícímu stejnému vlastnímu číslu λ je vlastní vektor se stejným vlastním číslem.
2. Vlastní vektory operátor A s párově odlišnými vlastními čísly λ 1 , λ 2 , …, λ m jsou lineárně nezávislé.
3. Jestliže vlastní čísla λ 1 =λ 2 = λ m = λ, pak vlastní číslo λ odpovídá nejvýše m lineárně nezávislých vlastních vektorů.

Pokud tedy existuje n lineárně nezávislých vlastních vektorů odpovídající různým vlastním číslům λ 1 , λ 2 , …, λ n , pak jsou lineárně nezávislé, proto je lze brát jako základ prostoru R n . Nalezněme tvar matice lineárního operátoru A na základě jeho vlastních vektorů, pro které jednáme s operátorem A na vektorech báze: Pak .
Matice lineárního operátoru A má tedy na základě svých vlastních vektorů diagonální tvar a vlastní hodnoty operátoru A jsou na diagonále.
Existuje jiný základ, ve kterém má matice diagonální tvar? Odpověď na tuto otázku dává následující věta.

Teorém. Matice lineárního operátoru A v bázi (i = 1..n) má diagonální tvar právě tehdy, když všechny vektory báze jsou vlastními vektory operátoru A.

Pravidlo pro hledání vlastních čísel a vlastních vektorů

Nechte vektor , kde x 1 , x 2 , …, x n - souřadnice vektoru vzhledem k bázi a je vlastním vektorem lineárního operátoru A odpovídajícím vlastnímu číslu λ, tj. . Tento vztah lze zapsat v maticovém tvaru

. (*)

Rovnici (*) lze považovat za rovnici pro nalezení , a , to znamená, že nás zajímá netriviální řešení, protože vlastní vektor nemůže být nulový. Je známo, že netriviální řešení homogenní systém lineární rovnice existují právě tehdy, když det(A - λE) = 0. Aby λ bylo vlastní hodnotou operátoru A, je nutné a postačující, aby det(A - λE) = 0.
Pokud je rovnice (*) napsána podrobně v souřadnicovém tvaru, dostaneme systém lineárních homogenních rovnic:

(1)
Kde je matice lineárního operátoru.

Soustava (1) má nenulové řešení, pokud je její determinant D roven nule

Dostali jsme rovnici pro hledání vlastních hodnot.
Tato rovnice se nazývá charakteristická rovnice a její levá strana se nazývá charakteristický polynom matice (operátor) A. Nemá-li charakteristický polynom žádné reálné kořeny, pak matice A nemá žádné vlastní vektory a nelze ji redukovat na diagonální tvar.
Nechť λ 1 , λ 2 , …, λ n jsou skutečné kořeny charakteristické rovnice a mohou mezi nimi být násobky. Dosazením těchto hodnot do systému (1) najdeme vlastní vektory.

Příklad 12. Lineární operátor A působí v R 3 podle zákona , kde x 1 , x 2 , .., x n jsou souřadnice vektoru v zákl. , , . Najděte vlastní čísla a vlastní vektory tohoto operátoru.
Řešení. Sestavíme matici tohoto operátoru:
.
Sestavíme systém pro určení souřadnic vlastních vektorů:

Sestavíme charakteristickou rovnici a vyřešíme ji:

.
λ 1,2 = -1, λ 3 = 3.
Dosazením λ = -1 do systému máme:
nebo
Protože , pak jsou dvě závislé proměnné a jedna volná proměnná.
Nechť x 1 je tedy volná neznámá Tuto soustavu vyřešíme libovolným způsobem a najdeme obecné řešení této soustavy: Základní soustava řešení se skládá z jednoho řešení, protože n - r = 3 - 2 = 1.
Množina vlastních vektorů odpovídajících vlastnímu číslu λ = -1 má tvar: , kde x 1 je libovolné číslo jiné než nula. Vyberme jeden vektor z této množiny, například nastavením x 1 = 1: .
Pokud budeme argumentovat podobně, najdeme vlastní vektor odpovídající vlastnímu číslu λ = 3: .
V prostoru R 3 se báze skládá ze tří lineárně nezávislých vektorů, ale my jsme získali pouze dva lineárně nezávislé vlastní vektory, ze kterých nelze bázi v R 3 vytvořit. V důsledku toho nelze matici A lineárního operátoru redukovat na diagonální tvar.

Příklad 13 Daná matrice .
1. Dokažte, že vektor je vlastním vektorem matice A. Najděte vlastní hodnotu odpovídající tomuto vlastnímu vektoru.
2. Najděte základ, ve kterém má matice A diagonální tvar.
Řešení.
1. Jestliže , pak je vlastní vektor

.
Vektor (1, 8, -1) je vlastní vektor. Vlastní číslo λ = -1.
Matice má diagonální tvar v bázi skládající se z vlastních vektorů. Jeden z nich je slavný. Pojďme najít zbytek.
Hledáme vlastní vektory ze systému:

Charakteristická rovnice: ;
(3 + A)[-2(2-A)(2+A)+3] = 0; (3+A)(A2-1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Najděte vlastní vektor odpovídající vlastnímu číslu λ = -3:

Hodnost matice této soustavy je rovna dvěma a rovná se počtu neznámých, proto má tato soustava pouze nulové řešení x 1 = x 3 = 0. x 2 zde může být cokoliv jiného než nula, např. x 2 = 1. Vektor (0 ,1,0) je tedy vlastním vektorem odpovídajícím λ = -3. Pojďme zkontrolovat:
.
Pokud λ = 1, pak dostaneme soustavu
Hodnost matice je dvě. Přeškrtni poslední rovnici.
Nechť x 3 je volná neznámá. Potom x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
Za předpokladu x 3 = 1 máme (-3,-9,1) - vlastní vektor odpovídající vlastnímu číslu λ = 1. Zkontrolujte:

.
Protože jsou vlastní čísla skutečná a různá, vektory jim odpovídající jsou lineárně nezávislé, takže je lze vzít jako základ v R 3 . Tedy v zákl , , matice A má tvar:
.
Ne každou matici lineárního operátoru A:R n → R n lze redukovat na diagonální formu, protože pro některé lineární operátory může být méně než n lineárně nezávislých vlastních vektorů. Pokud je však matice symetrická, pak přesně m lineárně nezávislých vektorů odpovídá kořenu charakteristické rovnice násobnosti m.

Definice. Symetrická matice je čtvercová matice, ve které jsou prvky, které jsou symetrické vzhledem k hlavní diagonále, stejné, tj.
Poznámky. 1. Všechny vlastní hodnoty symetrické matice jsou reálné.
2. Vlastní vektory symetrické matice odpovídající párově různým vlastním číslům jsou ortogonální.
Za jednu z četných aplikací studovaného aparátu považujeme problém určení tvaru křivky druhého řádu.

www.stránka vám umožní najít. Stránka provádí výpočet. Během několika sekund server nabídne správné řešení. Charakteristická rovnice pro matici bude algebraický výraz nalezený pravidlem pro výpočet determinantu matrice matrice, zatímco na hlavní diagonále budou rozdíly v hodnotách prvků úhlopříčky a proměnné. Při počítání charakteristická rovnice pro matici online, každý prvek matrice budou násobeny odpovídajícími dalšími prvky matrice. Najít v režimu online možné pouze pro čtverec matrice. Najít operaci charakteristická rovnice pro matici online redukuje na výpočet algebraického součtu součinu prvků matrice v důsledku nalezení determinantu matrice, pouze za účelem určení charakteristická rovnice pro matici online. Tato operace zaujímá v teorii zvláštní místo matrice, umožňuje najít vlastní čísla a vektory pomocí kořenů. Hledání úkolu charakteristická rovnice pro matici online je množit prvky matrice s následným sečtením těchto produktů podle určitého pravidla. www.stránka najde charakteristická rovnice pro matici daný rozměr v režimu online. výpočet charakteristická rovnice pro matici online pro danou dimenzi je to nalezení polynomu s číselnými nebo symbolickými koeficienty nalezenými pravidlem pro výpočet determinantu matrice- jako součet součinů odpovídajících prvků matrice, pouze za účelem určení charakteristická rovnice pro matici online. Hledání polynomu vzhledem k proměnné pro čtverec matrice, jako definice charakteristická rovnice pro matici, teoreticky běžné matrice. Hodnota kořenů polynomu charakteristická rovnice pro matici online používá se k definování vlastních vektorů a vlastních hodnot pro matrice. Pokud však determinant matrice bude tedy nula maticová charakteristická rovnice bude stále existovat, na rozdíl od opačného matrice. Aby bylo možné počítat charakteristická rovnice pro matici nebo hledejte několik najednou matice charakteristické rovnice, musíte strávit spoustu času a úsilí, zatímco náš server najde charakteristická rovnice pro online matici. V tomto případě odpověď nalezením charakteristická rovnice pro matici online budou správné a s dostatečnou přesností, i když čísla při nálezu charakteristická rovnice pro matici online bude iracionální. Na stránce www.stránka v prvcích jsou povoleny znaky matrice, to je charakteristická rovnice pro online matici lze při výpočtu znázornit v obecné symbolické formě matice charakteristických rovnic online. Získanou odpověď je užitečné zkontrolovat při řešení problému hledání charakteristická rovnice pro matici online pomocí webu www.stránka. Při provádění operace výpočtu polynomu - charakteristická rovnice matice, je nutné být při řešení tohoto problému pozorný a maximálně koncentrovaný. Naše stránky vám zase pomohou zkontrolovat vaše rozhodnutí o tématu matice charakteristických rovnic online. Pokud nemáte čas na dlouhé kontroly vyřešených problémů, tak www.stránka bude jistě vhodným nástrojem pro kontrolu při hledání a výpočtu charakteristická rovnice pro matici online.