Der Modus einer diskreten Zufallsvariablen ist ihr Wert. Median und Modus einer kontinuierlichen Zufallsvariablen

Unter den numerischen Merkmalen von Zufallsvariablen sind zunächst diejenigen zu erwähnen, die die Position der Zufallsvariablen auf der Zahlenachse charakterisieren, d.h. Geben Sie einen durchschnittlichen, ungefähren Wert an, um den herum alle möglichen Werte einer Zufallsvariablen gruppiert sind.

Durchschnittswert Zufallsvariable es gibt eine bestimmte Zahl, die sozusagen ihr „Repräsentant“ ist und sie in groben Näherungsberechnungen ersetzt. Wenn wir sagen: „Die durchschnittliche Lampenbetriebszeit beträgt 100 Stunden“ oder „Der durchschnittliche Auftreffpunkt ist relativ zum Ziel um 2 m nach rechts verschoben“, bezeichnen wir eine bestimmte numerische Eigenschaft einer Zufallsvariablen, die ihren Standort beschreibt auf der Zahlenachse, d.h. „Positionsmerkmale“.

Von den Merkmalen einer Position in der Wahrscheinlichkeitstheorie spielt der mathematische Erwartungswert einer Zufallsvariablen die wichtigste Rolle, die manchmal einfach als Durchschnittswert einer Zufallsvariablen bezeichnet wird.

Betrachten wir eine diskrete Zufallsvariable mit möglichen Werten und Wahrscheinlichkeiten. Wir müssen die Position der Werte einer Zufallsvariablen auf der x-Achse mit einer Zahl charakterisieren und dabei berücksichtigen, dass diese Werte unterschiedliche Wahrscheinlichkeiten haben. Zu diesem Zweck ist es selbstverständlich, den sogenannten „gewichteten Durchschnitt“ der Werte zu verwenden, und jeder Wert sollte bei der Mittelung mit einem „Gewicht“ berücksichtigt werden, das proportional zur Wahrscheinlichkeit dieses Werts ist. Daher berechnen wir den Durchschnitt der Zufallsvariablen, den wir wie folgt bezeichnen:

oder, vorausgesetzt,

. (5.6.1)

Dieser gewichtete Durchschnitt wird als mathematischer Erwartungswert der Zufallsvariablen bezeichnet. Damit haben wir eines der wichtigsten Konzepte der Wahrscheinlichkeitstheorie in Betracht gezogen – das Konzept mathematische Erwartung.

Der mathematische Erwartungswert einer Zufallsvariablen ist die Summe der Produkte aller möglichen Werte einer Zufallsvariablen und der Wahrscheinlichkeiten dieser Werte.

Beachten Sie, dass in der obigen Formulierung die Definition des mathematischen Erwartungswerts streng genommen nur für diskrete Zufallsvariablen gilt; Im Folgenden werden wir dieses Konzept auf den Fall kontinuierlicher Größen verallgemeinern.

Um das Konzept der mathematischen Erwartung klarer zu machen, wenden wir uns der mechanischen Interpretation der Verteilung einer diskreten Zufallsvariablen zu. Es gebe Punkte mit Abszissen auf der Abszissenachse, in denen jeweils die Massen konzentriert sind, und . Dann ist die durch die Formel (5.6.1) definierte mathematische Erwartung offensichtlich nichts anderes als die Abszisse des Schwerpunkts eines gegebenen Systems materieller Punkte.

Der mathematische Erwartungswert einer Zufallsvariablen ist durch eine eigentümliche Abhängigkeit mit dem arithmetischen Mittel der beobachteten Werte der Zufallsvariablen über eine Vielzahl von Experimenten verbunden. Diese Abhängigkeit ist von der gleichen Art wie die Abhängigkeit zwischen Häufigkeit und Wahrscheinlichkeit, nämlich: Bei einer großen Anzahl von Experimenten nähert sich das arithmetische Mittel der beobachteten Werte einer Zufallsvariablen ihrem mathematischen Erwartungswert (konvergiert in der Wahrscheinlichkeit). Aus dem Vorliegen eines Zusammenhangs zwischen Häufigkeit und Wahrscheinlichkeit lässt sich als Konsequenz auf das Vorliegen eines ähnlichen Zusammenhangs zwischen dem arithmetischen Mittel und dem mathematischen Erwartungswert schließen.

Betrachten Sie tatsächlich eine diskrete Zufallsvariable, die durch eine Verteilungsreihe gekennzeichnet ist:

Wo .

Lassen Sie unabhängige Experimente durchführen, bei denen die Menge jeweils einen bestimmten Wert annimmt. Nehmen wir an, dass der Wert einmal vorkam, der Wert einmal vorkam und der Wert einmal vorkam. Offensichtlich,

Berechnen wir das arithmetische Mittel der beobachteten Werte der Größe, das wir im Gegensatz zur mathematischen Erwartung bezeichnen:

Aber es gibt nichts weiter als die Häufigkeit (oder statistische Wahrscheinlichkeit) eines Ereignisses; Diese Frequenz kann bezeichnet werden. Dann

,

diese. das arithmetische Mittel der beobachteten Werte einer Zufallsvariablen ist gleich der Summe der Produkte aller möglichen Werte der Zufallsvariablen und der Häufigkeiten dieser Werte.

Mit zunehmender Anzahl der Experimente nähern sich die Häufigkeiten den entsprechenden Wahrscheinlichkeiten an (konvergieren in der Wahrscheinlichkeit). Folglich wird sich das arithmetische Mittel der beobachteten Werte einer Zufallsvariablen mit zunehmender Anzahl von Experimenten ihrem mathematischen Erwartungswert annähern (in der Wahrscheinlichkeit konvergieren).

Der oben formulierte Zusammenhang zwischen dem arithmetischen Mittel und der mathematischen Erwartung bildet den Inhalt einer der Formen des Gesetzes der großen Zahlen. Wir werden in Kapitel 13 einen strengen Beweis dieses Gesetzes liefern.

Wir wissen bereits, dass alle Formen des Gesetzes der großen Zahlen die Tatsache besagen, dass einige Durchschnittswerte über eine große Anzahl von Experimenten hinweg stabil sind. Hier geht es um die Stabilität des arithmetischen Mittels aus einer Reihe von Beobachtungen gleicher Größe. Bei einer kleinen Anzahl von Experimenten ist das arithmetische Mittel ihrer Ergebnisse zufällig; Bei ausreichender Erhöhung der Anzahl der Experimente wird es „fast nicht zufällig“ und nähert sich stabilisierend einem konstanten Wert – der mathematischen Erwartung.

Die Stabilität von Mittelwerten über eine große Anzahl von Experimenten kann experimentell leicht überprüft werden. Zum Beispiel beim Wiegen eines Körpers in einem Labor präzise Waagen Durch das Wiegen erhalten wir jedes Mal einen neuen Wert. Um Beobachtungsfehler zu reduzieren, wiegen wir den Körper mehrmals und verwenden das arithmetische Mittel der erhaltenen Werte. Es ist leicht zu erkennen, dass mit einer weiteren Erhöhung der Anzahl der Experimente (Wägungen) das arithmetische Mittel immer weniger auf diese Erhöhung reagiert und sich bei einer ausreichend großen Anzahl von Experimenten praktisch nicht mehr ändert.

Formel (5.6.1) für den mathematischen Erwartungswert entspricht dem Fall einer diskreten Zufallsvariablen. Für kontinuierlicher Wert Die mathematische Erwartung wird natürlich nicht als Summe, sondern als Integral ausgedrückt:

, (5.6.2)

Wo ist die Verteilungsdichte der Menge?

Formel (5.6.2) ergibt sich aus Formel (5.6.1), wenn die darin enthaltenen Einzelwerte durch einen sich kontinuierlich ändernden Parameter x, die entsprechenden Wahrscheinlichkeiten – durch das Wahrscheinlichkeitselement und die Endsumme – durch das Integral ersetzt werden. In Zukunft werden wir diese Methode häufig verwenden, um die für diskontinuierliche Größen abgeleiteten Formeln auf den Fall kontinuierlicher Größen zu erweitern.

In der mechanischen Interpretation behält die mathematische Erwartung einer kontinuierlichen Zufallsvariablen dieselbe Bedeutung – die Abszisse des Schwerpunkts für den Fall, dass die Masse entlang der Abszisse kontinuierlich mit Dichte verteilt ist. Diese Interpretation ermöglicht es oft, den mathematischen Erwartungswert zu finden, ohne das Integral (5.6.2) aus einfachen mechanischen Überlegungen zu berechnen.

Oben haben wir eine Notation für den mathematischen Erwartungswert der Größe eingeführt. Wenn eine Größe in Formeln als bestimmte Zahl angegeben wird, ist es in einigen Fällen bequemer, sie mit einem Buchstaben zu bezeichnen. In diesen Fällen bezeichnen wir den mathematischen Erwartungswert eines Wertes durch:

Die Notationen und für den mathematischen Erwartungswert werden in Zukunft parallel verwendet, abhängig von der Zweckmäßigkeit einer bestimmten Aufzeichnung der Formeln. Vereinbaren wir gegebenenfalls auch die Abkürzung der Wörter „mathematische Erwartung“ mit den Buchstaben m.o.

Dabei ist zu beachten, dass das wichtigste Merkmal einer Position – der mathematische Erwartungswert – nicht für alle Zufallsvariablen existiert. Es ist möglich, Beispiele für solche Zufallsvariablen zusammenzustellen, für die der mathematische Erwartungswert nicht besteht, da die entsprechende Summe oder das entsprechende Integral divergiert.

Betrachten Sie zum Beispiel eine diskontinuierliche Zufallsvariable mit einer Verteilungsreihe:

Das lässt sich leicht überprüfen, d.h. die Vertriebsreihe macht Sinn; Allerdings weicht die Summe in diesem Fall ab und daher gibt es keinen mathematischen Erwartungswert für den Wert. Für die Praxis sind solche Fälle jedoch nicht von nennenswertem Interesse. Typischerweise haben die Zufallsvariablen, mit denen wir uns befassen, einen begrenzten Bereich möglicher Werte und natürlich einen mathematischen Erwartungswert.

Oben haben wir die Formeln (5.6.1) und (5.6.2) angegeben, die den mathematischen Erwartungswert für eine diskontinuierliche bzw. kontinuierliche Zufallsvariable ausdrücken.

Wenn die Menge zu den Mengen gehört gemischter Typ, dann wird seine mathematische Erwartung durch eine Formel der Form ausgedrückt:

, (5.6.3)

Dabei erstreckt sich die Summe auf alle Punkte, an denen die Verteilungsfunktion unstetig ist, und das Integral erstreckt sich auf alle Bereiche, in denen die Verteilungsfunktion stetig ist.

Neben dem wichtigsten Merkmal einer Position – dem mathematischen Erwartungswert – werden in der Praxis manchmal auch andere Merkmale der Position verwendet, insbesondere der Modus und der Median einer Zufallsvariablen.

Der Modus einer Zufallsvariablen ist ihr wahrscheinlichster Wert. Der Begriff „wahrscheinlichster Wert“ gilt streng genommen nur für diskontinuierliche Größen; Bei einer kontinuierlichen Größe ist der Modus der Wert, bei dem die Wahrscheinlichkeitsdichte maximal ist. Wir vereinbaren, den Modus mit dem Buchstaben zu bezeichnen. In Abb. 5.6.1 und 5.6.2 zeigen den Modus für diskontinuierliche bzw. kontinuierliche Zufallsvariablen.

Wenn das Verteilungspolygon (Verteilungskurve) mehr als ein Maximum aufweist, wird die Verteilung als „multimodal“ bezeichnet (Abb. 5.6.3 und 5.6.4).

Manchmal gibt es Verteilungen, die in der Mitte ein Minimum statt eines Maximums haben (Abb. 5.6.5 und 5.6.6). Solche Verteilungen werden „antimodal“ genannt. Ein Beispiel für eine antimodale Verteilung ist die in Beispiel 5, Nr. 5.1 erhaltene Verteilung.

IN allgemeiner Fall Modus und mathematische Erwartung einer Zufallsvariablen stimmen nicht überein. Im Einzelfall, wenn die Verteilung symmetrisch und modal ist (d. h. einen Modus hat) und eine mathematische Erwartung besteht, dann stimmt sie mit dem Modus und dem Symmetriezentrum der Verteilung überein.

Häufig wird ein weiteres Positionsmerkmal verwendet – der sogenannte Median einer Zufallsvariablen. Dieses Merkmal wird normalerweise nur für kontinuierliche Zufallsvariablen verwendet, obwohl es formal für eine diskontinuierliche Variable definiert werden kann.

Der Median einer Zufallsvariablen ist ihr Wert für die

diese. Es ist gleichermaßen wahrscheinlich, dass die Zufallsvariable kleiner oder größer ist. Geometrisch gesehen ist der Median die Abszisse des Punktes, an dem die durch die Verteilungskurve begrenzte Fläche halbiert wird (Abb. 5.6.7).

Neben dem mathematischen Erwartungswert und der Streuung verwendet die Wahrscheinlichkeitstheorie eine Reihe numerischer Merkmale, die bestimmte Merkmale der Verteilung widerspiegeln.

Definition. Der Modus Mo(X) einer Zufallsvariablen X ist ihr wahrscheinlichster Wert(für die die Wahrscheinlichkeit r g oder Wahrscheinlichkeitsdichte

Erreicht die Wahrscheinlichkeit bzw. Wahrscheinlichkeitsdichte nicht an einem, sondern an mehreren Punkten ein Maximum, spricht man von einer Verteilung multimodal(Abb. 3.13).

Mode Moos), mit welcher Wahrscheinlichkeit P( oder die Wahrscheinlichkeitsdichte (p(x) erreicht ein globales Maximum) heißt höchstwahrscheinlich Bedeutung Zufallsvariable (in Abb. 3.13 ist dies Mo(X) 2).

Definition. Der Median Ме(Х) einer kontinuierlichen Zufallsvariablen X ist ihr Wert, wofür

diese. die Wahrscheinlichkeit, dass die Zufallsvariable X nimmt einen Wert an, der kleiner als der Median ist Fell) oder größer ist, ist gleich und gleich 1/2. Geometrisch vertikale Gerade X = Fell), der durch einen Punkt mit einer Abszisse gleich verläuft Fell), teilt die Fläche der Figur Jod der Verteilungskurve in zwei gleiche Teile (Abb. 3.14). Offensichtlich an der Stelle X = Fell) die Verteilungsfunktion ist gleich 1/2, d.h. P(Me(X))= 1/2 (Abb. 3.15).

Beachten wir eine wichtige Eigenschaft des Medians einer Zufallsvariablen: der mathematische Erwartungswert des Absolutwerts der Abweichung der Zufallsvariablen X vom konstanten Wert C ist dann minimal, wenn diese Konstante C gleich dem Median Me(X) = m ist, d.h.

(Die Eigenschaft ähnelt der Eigenschaft (3.10") des minimalen Quadrats der Abweichung einer Zufallsvariablen von ihrem mathematischen Erwartungswert.)

O Beispiel 3.15. Finden Sie den Modus, den Median und den mathematischen Erwartungswert einer Zufallsvariablen X s Wahrscheinlichkeitsdichte f(x) = 3x 2 für xx.

Lösung. Die Verteilungskurve ist in Abb. dargestellt. 3.16. Offensichtlich ist die Wahrscheinlichkeitsdichte φ(x) maximal bei X= Mo(X) = 1.

Mittlere Fell) = B wir finden aus Bedingung (3.28):

Wo

Berechnen wir den mathematischen Erwartungswert mithilfe der Formel (3.25):

Gegenseitige Anordnung der Punkte M(X)>Me(X) Und Moos) in aufsteigender Reihenfolge der Abszisse ist in Abb. dargestellt. 3.16. ?

Neben den oben genannten numerischen Merkmalen werden zur Beschreibung einer Zufallsvariablen auch die Konzepte der Quantile und Prozentpunkte verwendet.

Definition. Quantilebene y-Quantil )

Dieser Wert wird x q einer Zufallsvariablen genannt , bei dem seine Verteilungsfunktion einen Wert gleich annimmt d, d.h.

Einige Quantile haben einen besonderen Namen erhalten. Offensichtlich wurde das oben Gesagte eingeführt mittlere Die Zufallsvariable ist ein Quantil der Stufe 0,5, d. h. Me(X) = x 05. Die Quantile dg 0 2 5 und x 075 wurden jeweils benannt untere Und oberes QuartilK

Eng mit dem Konzept des Quantils verbunden ist das Konzept Prozentpunkt. Unter YuOuHo-noy Punkt Quantil ist impliziert x x (( , diese. ist der Wert der Zufallsvariablen X, bei dem

0 Beispiel 3.16. Ermitteln Sie anhand der Daten in Beispiel 3.15 das Quantil x 03 und der 30 %-Punkt der Zufallsvariablen X.

Lösung. Nach Formel (3.23) ist die Verteilungsfunktion

Das Quantil 0 s finden wir aus Gleichung (3.29), d.h. x$ 3 =0,3, daher L "oz -0,67. Finden wir den 30%-Punkt der Zufallsvariablen X, oder Quantil x 0 7, aus Gl. x$ 7 = 0,7, von wo x 0 7 «0,89. ?

Unter den numerischen Merkmalen einer Zufallsvariablen sind Momente – Anfangs- und Zentralmomente – von besonderer Bedeutung.

Definition. Der StartmomentDie k-te Ordnung einer Zufallsvariablen X wird als mathematischer Erwartungswert bezeichnet Abschluss diesen Wert :

Definition. Zentraler MomentDie k-te Ordnung einer Zufallsvariablen X ist die mathematische Erwartung des k-ten Grades der Abweichung einer Zufallsvariablen X von ihrer mathematischen Erwartung:

Formeln zur Berechnung von Momenten für diskrete Zufallsvariablen (Werte nehmen). x 1 mit Wahrscheinlichkeiten p,) und kontinuierlich (mit Wahrscheinlichkeitsdichte cp(x)) sind in der Tabelle angegeben. 3.1.

Tabelle 3.1

Es ist leicht zu bemerken, wann k = 1 erstes Anfangsmoment einer Zufallsvariablen X ist seine mathematische Erwartung, d.h. h x = M[X) = a, bei Zu= 2 Sekunden Zentralmoment - Streuung, d.h. p 2 = T)(X).

Die zentralen Momente p A können durch die Anfangsmomente ausgedrückt werden, aber durch die Formeln:

usw.

Zum Beispiel c 3 = M(X-a)* = M(X*-ZaX 2 +Za 2 X-a->) = M(X*)~ -ZaM(X 2)+Za 2 M(X)~ a3 = y 3 -Зу^ + Зу(у, -у^ = y 3 - Зу^ + 2у^ (bei der Ableitung haben wir das berücksichtigt A = M(X)= V, ist ein nicht zufälliger Wert). ?

Oben wurde darauf hingewiesen, dass die mathematische Erwartung M(X), oder der erste Anfangszeitpunkt, charakterisiert den Durchschnittswert oder die Position, das Zentrum der Verteilung einer Zufallsvariablen X auf der Zahlenachse; Streuung OH), oder das zweite zentrale Moment p 2, - s t s - Verteilungsdispersionsstumpf X relativ M(X). Für mehr ausführliche Beschreibung Verteilungen dienen als Momente höherer Ordnung.

Dritter zentraler Punkt p 3 dient zur Charakterisierung der Asymmetrie (Schiefe) der Verteilung. Es hat die Dimension eines zufälligen Würfels. Um eine dimensionslose Größe zu erhalten, wird sie durch o 3 dividiert, wobei a die Standardabweichung der Zufallsvariablen ist X. Der resultierende Wert A angerufen Asymmetriekoeffizient einer Zufallsvariablen.

Wenn die Verteilung relativ zur mathematischen Erwartung symmetrisch ist, dann ist der Asymmetriekoeffizient A = 0.

In Abb. Abbildung 3.17 zeigt zwei Verteilungskurven: I und II. Kurve I hat eine positive (rechtsseitige) Asymmetrie (L > 0) und Kurve II hat eine negative (linksseitige) Asymmetrie (L).

Vierter zentraler Punkt p 4 dient zur Charakterisierung der Steilheit (Schärfe oder Flachheit) der Verteilung.

Mathematische Erwartung. Mathematische Erwartung diskrete Zufallsvariable X, wobei eine endliche Anzahl von Werten angenommen wird Xich mit Wahrscheinlichkeiten Rich, der Betrag heißt:

Mathematische Erwartung kontinuierliche Zufallsvariable X heißt das Integral des Produkts seiner Werte X auf der WahrF(X):

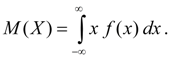(6B)

Uneigentliches Integral (6 B) wird als absolut konvergent angenommen (ansonsten sagt man, dass die mathematische Erwartung M(X) existiert nicht). Die mathematische Erwartung charakterisiert Durchschnittswert Zufallsvariable X. Seine Dimension stimmt mit der Dimension der Zufallsvariablen überein.

Eigenschaften der mathematischen Erwartung:

Streuung. Varianz Zufallsvariable X die Nummer heißt:

Die Varianz ist Streucharakteristik Zufallsvariablenwerte X relativ zu seinem Durchschnittswert M(X). Die Varianzdimension ist gleich der Dimension der Zufallsvariablen im Quadrat. Basierend auf den Definitionen der Varianz (8) und des mathematischen Erwartungswerts (5) für eine diskrete Zufallsvariable und (6) für eine kontinuierliche Zufallsvariable erhalten wir ähnliche Ausdrücke für die Varianz:

(9)

Hier M = M(X).

Dispersionseigenschaften:

Standardabweichung:

(11)

Da die Standardabweichung die gleiche Dimension wie eine Zufallsvariable hat, wird sie häufiger als Maß für die Streuung als für die Varianz verwendet.

Momente der Verteilung. Die Konzepte des mathematischen Erwartungswerts und der Streuung sind Sonderfälle von mehr allgemeines Konzept für numerische Eigenschaften von Zufallsvariablen – Verteilungsmomente. Die Verteilungsmomente einer Zufallsvariablen werden als mathematische Erwartungen einiger einfacher Funktionen einer Zufallsvariablen eingeführt. Also, Moment der Ordnung k relativ zum Punkt X 0 wird als mathematischer Erwartungswert bezeichnet M(X–X 0 )k. Momente über den Ursprung X= 0 aufgerufen werden erste Momente und werden bezeichnet:

(12)

Das Anfangsmoment erster Ordnung ist das Zentrum der Verteilung der betrachteten Zufallsvariablen:

(13)

Momente über das Verteilungszentrum X= M werden aufgerufen zentrale Punkte und werden bezeichnet:

(14)

Aus (7) folgt, dass das Zentralmoment erster Ordnung immer gleich Null ist:

Die zentralen Momente hängen nicht vom Ursprung der Werte der Zufallsvariablen ab, da sie um einen konstanten Wert verschoben werden MIT sein Verteilungsschwerpunkt verschiebt sich um den gleichen Wert MIT, und die Abweichung vom Zentrum ändert sich nicht: X – M = (X – MIT) – (M – MIT).
Jetzt ist es offensichtlich Streuung- Das Zentralmoment zweiter Ordnung:

Asymmetrie. Zentrales Moment dritter Ordnung:

(17)

dient der Auswertung Verteilungsasymmetrien. Wenn die Verteilung symmetrisch zum Punkt ist X= M, dann ist das Zentralmoment dritter Ordnung gleich Null (wie alle Zentralmomente ungerader Ordnung). Wenn also das Zentralmoment dritter Ordnung von Null verschieden ist, kann die Verteilung nicht symmetrisch sein. Das Ausmaß der Asymmetrie wird dimensionslos beurteilt Asymmetriekoeffizient:

(18)

Das Vorzeichen des Asymmetriekoeffizienten (18) zeigt eine rechts- oder linksseitige Asymmetrie an (Abb. 2).

Reis. 2. Arten der Verteilungsasymmetrie.

Überschuss. Zentraler Moment vierte Ordnung:

(19)

dient der Auswertung der sogenannten Überschuss, der den Grad der Steilheit (Spitzigkeit) der Verteilungskurve nahe der Mitte der Verteilung im Verhältnis zur Kurve bestimmt Normalverteilung. Da für eine Normalverteilung der als Kurtosis angenommene Wert ist:

(20)

In Abb. 3 zeigt Beispiele für Verteilungskurven mit verschiedene BedeutungenÜberschuss. Für Normalverteilung E= 0. Kurven, die spitzer als normal sind, haben eine positive Kurtosis, Kurven mit flacheren Spitzen haben eine negative Kurtosis.

Reis. 3. Verteilungskurven mit unterschiedlicher Steilheit (Kurtosis).

Momente höherer Ordnung werden in technischen Anwendungen der mathematischen Statistik normalerweise nicht verwendet.

Mode diskret Eine Zufallsvariable ist ihr wahrscheinlichster Wert. Mode kontinuierlich Eine Zufallsvariable ist ihr Wert, bei dem die Wahrscheinlichkeitsdichte maximal ist (Abb. 2). Wenn die Verteilungskurve ein Maximum hat, wird die Verteilung aufgerufen unimodal. Wenn eine Verteilungskurve mehr als ein Maximum aufweist, wird die Verteilung aufgerufen multimodal. Manchmal gibt es Verteilungen, deren Kurven ein Minimum anstelle eines Maximums aufweisen. Solche Verteilungen heißen antimodal. Im allgemeinen Fall stimmen Modus und mathematische Erwartung einer Zufallsvariablen nicht überein. Im Sonderfall, z modal, d.h. eine modussymmetrische Verteilung aufweist und sofern eine mathematische Erwartung vorliegt, stimmt diese mit dem Modus und dem Symmetriezentrum der Verteilung überein.

Mittlere Zufallsvariable X- das ist seine Bedeutung Meh, für die Gleichheit gilt: d.h. es ist ebenso wahrscheinlich, dass die Zufallsvariable X wird weniger oder mehr sein Meh. Geometrisch mittlere ist die Abszisse des Punktes, an dem die Fläche unter der Verteilungskurve in zwei Hälften geteilt wird (Abb. 2). Bei einer symmetrischen Modalverteilung sind Median, Modus und mathematischer Erwartungswert gleich.

Mode() einer kontinuierlichen Zufallsvariablen ist ihr Wert, der dem Maximalwert ihrer Wahrscheinlichkeitsdichte entspricht.

Mittlere() Eine kontinuierliche Zufallsvariable ist ihr Wert, der durch die Gleichheit bestimmt wird:

B15. Binomialgesetz Verteilungen und ihre numerischen Eigenschaften. Binomialverteilung beschreibt wiederholte unabhängige Experimente. Dieses Gesetz bestimmt den Eintritt eines Ereignisses einmalig unabhängige Tests, wenn sich die Wahrscheinlichkeit des Eintretens eines Ereignisses in jedem dieser Experimente von Experiment zu Experiment nicht ändert. Wahrscheinlichkeit:

,

wobei: die bekannte Wahrscheinlichkeit des Eintretens eines Ereignisses in einem Experiment ist, die sich von Experiment zu Experiment nicht ändert;

– Wahrscheinlichkeit des Nichteintretens eines Ereignisses im Experiment;

– die angegebene Häufigkeit des Auftretens des Ereignisses in den Experimenten;

– Anzahl der Kombinationen von Elementen durch .

B15. Gleichverteilungsgesetz, Diagramme der Verteilungsfunktion und -dichte, numerische Eigenschaften. Es wird eine kontinuierliche Zufallsvariable betrachtet gleichmäßig verteilt, wenn seine Wahrscheinlichkeitsdichte die Form hat:

Erwartung Zufallsvariable mit Gleichverteilung:

Streuung lässt sich wie folgt berechnen:

Standardabweichung wird so aussehen:

.

B17. Exponentielles Verteilungsgesetz, Diagramme der Verteilungsfunktion und -dichte, numerische Eigenschaften. Exponentielle Verteilung Eine kontinuierliche Zufallsvariable ist eine Verteilung, die durch den folgenden Ausdruck für die Wahrscheinlichkeitsdichte beschrieben wird:

,

wo ist ein konstanter positiver Wert.

Die Wahrschat in diesem Fall die Form:

Die mathematische Erwartung einer Zufallsvariablen mit einer Exponentialverteilung wird basierend auf erhalten allgemeine Formel unter Berücksichtigung dessen, wenn:

.

Wenn wir diesen Ausdruck nach Teilen integrieren, finden wir: .

Die Varianz für die Exponentialverteilung kann mit folgendem Ausdruck ermittelt werden:

.

Wenn wir den Ausdruck für die Wahrscheinlichkeitsdichte einsetzen, finden wir:

Wenn wir das Integral nach Teilen berechnen, erhalten wir: .

B16. Normalverteilungsgesetz, Diagramme der Verteilungsfunktion und Dichte. Standardnormalverteilung. Reflektierte Normalverteilungsfunktion. Normal Man nennt eine solche Verteilung einer Zufallsvariablen, deren Wahrscheinlichkeitsdichte durch die Gaußsche Funktion beschrieben wird:

wo ist die Standardabweichung;

– mathematische Erwartung einer Zufallsvariablen.

Der Dichtegraph einer Normalverteilung wird als normale Gaußsche Kurve bezeichnet.

B18. Markovs Ungleichung. Verallgemeinerte Tschebyscheff-Ungleichung. Wenn für eine Zufallsvariable X existiert, dann gilt es für jeden Markov-Ungleichung .

Es folgt aus verallgemeinerte Tschebyscheff-Ungleichung: Die Funktion sei monoton wachsend und nicht negativ auf . Wenn für eine Zufallsvariable X existiert, dann gilt die Ungleichung für jeden .

B19. Das Gesetz der großen Zahlen in Tschebyscheff-Form. Seine Bedeutung. Folgerung des Gesetzes der großen Zahlen in Tschebyscheff-Form. Gesetz der großen Zahlen in Bernoulli-Form. Unter Gesetz der großen Zahlen In der Wahrscheinlichkeitstheorie werden eine Reihe von Theoremen verstanden, die jeweils die Tatsache der asymptotischen Annäherung des Durchschnittswerts einer großen Anzahl experimenteller Daten an den mathematischen Erwartungswert einer Zufallsvariablen belegen. Die Beweise dieser Theoreme basieren auf der Tschebyscheff-Ungleichung. Diese Ungleichung kann durch die Betrachtung einer diskreten Zufallsvariablen mit möglichen Werten erhalten werden.

Satz. Es gebe eine endliche Folge unabhängige Zufallsvariablen mit demselben mathematischen Erwartungswert und denselben Varianzen, begrenzt durch dieselbe Konstante:

Dann ist die Wahrscheinlichkeit des Ereignisses unabhängig von der Zahl

tendiert zur Einheit bei .

Der Satz von Tschebyschew stellt eine Verbindung zwischen der Wahrscheinlichkeitstheorie, die die durchschnittlichen Eigenschaften der gesamten Wertemenge einer Zufallsvariablen berücksichtigt, und der mathematischen Statistik her, die mit einer begrenzten Wertemenge dieser Variablen arbeitet. Es zeigt, dass sich bei einer ausreichend großen Anzahl von Messungen einer bestimmten Zufallsvariablen das arithmetische Mittel der Werte dieser Messungen dem mathematischen Erwartungswert annähert.

B20. Gegenstand und Aufgaben der mathematischen Statistik. Allgemeine und Stichprobenpopulationen. Auswahlmethode. Mathematische Statistik– die Wissenschaft von mathematische Methoden Systematisierung und Nutzung statistischer Daten für wissenschaftliche und praktische Schlussfolgerungen auf der Grundlage der Wahrscheinlichkeitstheorie.

Gegenstand der mathematischen Statistik sind zufällige Ereignisse, Größen und Funktionen, die das betrachtete Zufallsphänomen charakterisieren. Die folgenden Ereignisse sind zufällig: Gewinn eines Lottoscheins, Übereinstimmung des kontrollierten Produkts mit den festgelegten Anforderungen, störungsfreier Betrieb des Fahrzeugs im ersten Betriebsmonat, Erfüllung des täglichen Arbeitsplans durch den Auftragnehmer.

Stichprobenpopulation bezeichnet eine Sammlung zufällig ausgewählter Objekte.

Allgemeine Bevölkerung Benennen Sie die Menge der Objekte, aus denen die Probe besteht.

B21. Auswahlmethoden.

Auswahlmethoden: 1 Auswahl, die keine Aufteilung der Gesamtbevölkerung in Teile erfordert. Dazu gehören a) einfache Zufallsstichproben ohne Wiederholung und b) einfache zufällige wiederholte Stichproben. 2) Selektion, bei der die Bevölkerung in Teile geteilt wird. Dazu gehören a) typische Auswahl, b) mechanische Auswahl und c) serielle Auswahl.

Einfach zufällig Dies wird als Auswahl bezeichnet, bei der Objekte einzeln aus der Population extrahiert werden.

Typisch Dies wird als Auswahl bezeichnet, bei der Objekte nicht aus der gesamten Population, sondern aus jedem ihrer „typischen“ Teile ausgewählt werden.

Mechanisch Dies nennt man Auswahl, bei der die Grundgesamtheit mechanisch in so viele Gruppen aufgeteilt wird, wie es Objekte gibt, die in die Stichprobe aufgenommen werden sollen, und aus jeder Gruppe ein Objekt ausgewählt wird.

Seriell Dies wird als Selektion bezeichnet, bei der Objekte nicht einzeln, sondern in „Serien“ aus der allgemeinen Bevölkerung ausgewählt und einer kontinuierlichen Untersuchung unterzogen werden.

B22. Statistische und Variationsreihen. Empirische Verteilungsfunktion und ihre Eigenschaften. Variationsreihen für diskrete und kontinuierliche Zufallsvariablen. Nehmen wir eine Stichprobe aus der Allgemeinbevölkerung und beobachten Sie den Wert des untersuchten Parameters einmal, einmal usw. Darüber hinaus die Stichprobengröße. Die beobachteten Werte werden aufgerufen Optionen, und die Reihenfolge der in aufsteigender Reihenfolge geschriebenen Optionen ist Variationsreihe . Die Anzahl der Beobachtungen wird aufgerufen Frequenzen, und ihre Beziehung zur Stichprobengröße - relative Häufigkeiten.Variationsreihe kann durch eine Tabelle dargestellt werden wie:

X			…..
N			….

Statistische Stichprobenverteilung Benennen Sie eine Liste von Optionen und ihre entsprechenden relativen Häufigkeiten. Statistische Verteilung kann dargestellt werden als:

X			…..
w			….

Wo sind die relativen Häufigkeiten?

Empirische Verteilungsfunktion Rufen Sie eine Funktion auf, die für jeden Wert x die relative Häufigkeit des Ereignisses X bestimmt

Mode– der Wert in einer Reihe von Beobachtungen, der am häufigsten vorkommt

Mo = X Mo + h Mo * (f Mo - f Mo-1) : ((f Mo - f Mo-1) + (f Mo - f Mo+1)),

Hier ist X Mo die linke Grenze des Modalintervalls, h Mo ist die Länge des Modalintervalls, f Mo-1 ist die Häufigkeit des prämodalen Intervalls, f Mo ist die Häufigkeit des Modalintervalls, f Mo+1 ist die Häufigkeit des postmodalen Intervalls.

Der Modus einer absolut kontinuierlichen Verteilung ist jeder Punkt des lokalen Maximums der Verteilungsdichte. Bei diskreten Verteilungen wird ein Modus als jeder Wert a i betrachtet, dessen Wahrscheinlichkeit p i größer ist als die Wahrscheinlichkeiten benachbarter Werte

Mittlere kontinuierliche Zufallsvariable X Sein Wert wird Me genannt, für den es gleich wahrscheinlich ist, dass die Zufallsvariable kleiner oder größer sein wird Meh, d.h.

M e =(n+1)/2 P(X < Ich) = P(X > Meh)

Gleichmäßig verteiltes NSV

Gleichmäßige Verteilung. Eine kontinuierliche Zufallsvariable heißt gleichmäßig auf dem Segment verteilt (), wenn ihre Verteilungsdichtefunktion (Abb. 1.6, A) hat die Form:

Bezeichnung: – SW ist gleichmäßig verteilt über .

Dementsprechend ist die Verteilungsfunktion auf dem Segment (Abb. 1.6, B):

Reis. 1.6. Funktionen einer gleichmäßig verteilten Zufallsvariablen auf [ A,B]: A– Wahrscheinlichkeitsdichten F(X); B– Ausschüttungen F(X)

Der mathematische Erwartungswert und die Streuung eines gegebenen SV werden durch die Ausdrücke bestimmt:

Aufgrund der Symmetrie der Dichtefunktion stimmt diese mit dem Median überein. Moden haben keine gleichmäßige Verteilung

Beispiel 4. Die Wartezeit auf eine Antwort auf einen Telefonanruf ist eine Zufallsvariable, die einem Gleichverteilungsgesetz im Bereich von 0 bis 2 Minuten folgt. Finden Sie die Integral- und Ddieser Zufallsvariablen.

27. Normales Gesetz der Wahrscheinlichkeitsverteilung

Eine kontinuierliche Zufallsvariable x hat eine Normalverteilung mit den Parametern: m,s > 0, wenn die Wahrdie Form hat:

wobei: m – mathematische Erwartung, s – Standardabweichung.

Die Normalverteilung wird nach dem deutschen Mathematiker Gauß auch Gauß-Verteilung genannt. Die Tatsache, dass eine Zufallsvariable eine Normalverteilung mit den Parametern m hat, wird wie folgt bezeichnet: N (m,s), wobei: m=a=M[X];

Sehr oft wird in Formeln der mathematische Erwartungswert mit bezeichnet A . Wenn eine Zufallsvariable nach dem Gesetz N(0,1) verteilt ist, dann nennt man sie eine normalisierte oder standardisierte Normalvariable. Die Verteilungsfunktion dafür hat die Form:

Der Dichtegraph einer Normalverteilung, der als Normalkurve oder Gaußkurve bezeichnet wird, ist in Abb. 5.4 dargestellt.

Reis. 5.4. Normalverteilungsdichte

Eigenschaften Zufallsvariable mit Normalverteilungsgesetz.

1. Wenn , dann ermitteln Sie die Wahrscheinlichkeit, dass dieser Wert in ein bestimmtes Intervall fällt ( x 1 ; x 2) wird die Formel verwendet:

2. Die Wahrscheinlichkeit, dass die Abweichung einer Zufallsvariablen von ihrer mathematischen Erwartung den Wert (in absoluten Werten) nicht überschreitet, ist gleich.