Binomialverteilung. Diskrete Verteilungen in MS EXCEL
Binomialverteilung- eine der wichtigsten Wahrscheinlichkeitsverteilungen für diskrete Änderungen zufällige Variable. Die Binomialverteilung ist die Wahrscheinlichkeitsverteilung einer Zahl M Fall A V N voneinander unabhängige Beobachtungen. Oft ein Ereignis A wird als „Erfolg“ der Beobachtung bezeichnet und das gegenteilige Ereignis als „Misserfolg“, aber diese Bezeichnung ist sehr willkürlich.
Begriffe der Binomialverteilung:
- insgesamt durchgeführt N Prüfungen, in denen die Veranstaltung A kann auftreten oder auch nicht;
- Fall A in jedem der Versuche kann mit der gleichen Wahrscheinlichkeit auftreten P;
- Die Tests sind voneinander unabhängig.
Die Wahrscheinlichkeit, dass in N Testveranstaltung A Exakt M Zeiten, kann mit der Bernoulli-Formel berechnet werden:
![]()
![]() ,
,
Wo P- die Wahrscheinlichkeit des Eintretens des Ereignisses A;
Q = 1 - P ist die Wahrscheinlichkeit, dass das gegenteilige Ereignis eintritt.
Lass es uns herausfinden warum die Binomialverteilung in der oben beschriebenen Weise mit der Bernoulli-Formel zusammenhängt . Ereignis - die Anzahl der Erfolge bei N Tests sind in eine Reihe von Optionen unterteilt, bei denen jeweils ein Erfolg erzielt wird M Prüfungen und Misserfolge - in N - M Tests. Erwägen Sie eine dieser Optionen: B1 . Nach der Regel der Wahrscheinlichkeitsaddition multiplizieren wir die Wahrscheinlichkeiten entgegengesetzter Ereignisse:
![]() ,
,
und wenn wir bezeichnen Q = 1 - P, Das
![]() .
.
Die gleiche Wahrscheinlichkeit wird jede andere Option haben, bei der M Erfolg und N - M Misserfolge. Die Anzahl solcher Optionen entspricht der Anzahl der möglichen Möglichkeiten N Testen Sie es M Erfolg.
Die Summe der Wahrscheinlichkeiten aller M Ereignisnummer A(Zahlen von 0 bis N) ist gleich eins:
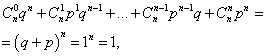
wobei jeder Term ein Term des Newton-Binoms ist. Daher wird die betrachtete Verteilung Binomialverteilung genannt.
In der Praxis ist es oft notwendig, Wahrscheinlichkeiten „höchstens“ zu berechnen M Erfolg in N Tests“ oder „zumindest M Erfolg in N Tests". Hierzu werden die folgenden Formeln verwendet.
Die Integralfunktion also Wahrscheinlichkeit F(M) das in N Beobachtungsereignis A wird nicht mehr kommen M einmal, kann nach folgender Formel berechnet werden:
Wiederum Wahrscheinlichkeit F(≥M) das in N Beobachtungsereignis A Komm wenigstens M einmal, wird nach der Formel berechnet:
Manchmal ist es bequemer, die Wahrscheinlichkeit zu berechnen, dass in N Beobachtungsereignis A wird nicht mehr kommen M mal durch die Wahrscheinlichkeit des entgegengesetzten Ereignisses:
![]() .
.
Welche der Formeln verwendet werden soll, hängt davon ab, welche davon weniger Terme enthält.
Die Eigenschaften der Binomialverteilung werden mit den folgenden Formeln berechnet .
Erwarteter Wert: .
Streuung: .
Standardabweichung: .
Binomialverteilung und Berechnungen in MS Excel
BinomP N ( M) und der Wert der Integralfunktion F(M) kann mit der MS Excel-Funktion BINOM.VERT berechnet werden. Das Fenster für die entsprechende Berechnung wird unten angezeigt (klicken Sie zum Vergrößern auf die linke Maustaste).

MS Excel erfordert die Eingabe folgender Daten:
- Anzahl der Erfolge;
- Anzahl der Tests;
- Erfolgswahrscheinlichkeit;
- Integral – logischer Wert: 0 – wenn Sie die Wahrscheinlichkeit berechnen müssen P N ( M) und 1 - wenn die Wahrscheinlichkeit F(M).
Beispiel 1 Der Manager des Unternehmens fasste Informationen zur Anzahl der in den letzten 100 Tagen verkauften Kameras zusammen. Die Tabelle fasst die Informationen zusammen und berechnet die Wahrscheinlichkeiten, dass eine bestimmte Anzahl Kameras pro Tag verkauft wird.
Der Tag endet mit einem Gewinn, wenn 13 oder mehr Kameras verkauft werden. Die Wahrscheinlichkeit, dass der Tag mit Gewinn ausgearbeitet wird:
![]()
Die Wahrscheinlichkeit, dass der Tag ohne Gewinn gearbeitet wird:
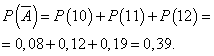
Die Wahrscheinlichkeit, dass der Tag einen Gewinn erwirtschaftet, sei konstant und gleich 0,61, und die Anzahl der pro Tag verkauften Kameras sei nicht vom Tag abhängig. Dann können Sie die Binomialverteilung verwenden, bei der das Ereignis auftritt A- Der Tag wird mit Gewinn ausgearbeitet, - ohne Gewinn.
Die Wahrscheinlichkeit, dass von 6 Tagen alle mit Gewinn abgearbeitet werden:
![]() .
.
Das gleiche Ergebnis erhalten wir mit der MS Excel-Funktion BINOM.VERT (der Wert des Integralwerts ist 0):
P 6 (6 ) = BINOM.VERT(6; 6; 0,61; 0) = 0,052.
Die Wahrscheinlichkeit, dass von 6 Tagen 4 oder mehr Tage mit Gewinn gearbeitet werden:
Wo ![]() ,
,
![]() ,
,
Mit der MS-Excel-Funktion BINOM.VERT berechnen wir die Wahrscheinlichkeit, dass von 6 Tagen nicht mehr als 3 Tage mit Gewinn abgeschlossen werden (der Wert des Integralwerts beträgt 1):
P 6 (≤3 ) = BINOM.VERT(3, 6, 0,61, 1) = 0,435.
Die Wahrscheinlichkeit, dass von 6 Tagen alle mit Verlusten auskommen:
![]() ,
,
Den gleichen Indikator berechnen wir mit der MS Excel-Funktion BINOM.VERT:
P 6 (0 ) = BINOM.VERT(0; 6; 0,61; 0) = 0,0035.
Lösen Sie das Problem selbst und sehen Sie dann die Lösung
Beispiel 2 Eine Urne enthält 2 weiße und 3 schwarze Kugeln. Eine Kugel wird aus der Urne genommen, die Farbe eingestellt und zurückgelegt. Der Versuch wird 5 Mal wiederholt. Die Häufigkeit des Auftretens weißer Kugeln ist eine diskrete Zufallsvariable X, verteilt nach dem Binomialgesetz. Stellen Sie das Verteilungsgesetz einer Zufallsvariablen auf. Definieren Sie die Mode erwarteter Wert und Streuung.
Wir lösen weiterhin gemeinsam Probleme
Beispiel 3 Vom Kurierdienst gingen die Gegenstände an N= 5 Kuriere. Jeder Kurier mit einer Wahrscheinlichkeit P= 0,3 ist unabhängig von den anderen zu spät für das Objekt. Diskrete Zufallsvariable X- die Anzahl der verspäteten Kuriere. Konstruieren Sie eine Verteilungsreihe dieser Zufallsvariablen. Finden Sie den mathematischen Erwartungswert, die Varianz und die Standardabweichung. Ermitteln Sie die Wahrscheinlichkeit, dass mindestens zwei Kuriere zu spät für die Objekte kommen.
Betrachten Sie die Binomialverteilung, berechnen Sie ihren mathematischen Erwartungswert, ihre Varianz und ihren Modus. Mit der MS-EXCEL-Funktion BINOM.DIST() zeichnen wir die Verteilungsfunktion und die Wahrscheinlichkeitsdichtediagramme. Schätzen wir den Verteilungsparameter p, den mathematischen Erwartungswert der Verteilung und die Standardabweichung. Betrachten Sie auch die Bernoulli-Verteilung.
Definition. Lass sie festgehalten werden N Tests, bei denen jeweils nur 2 Ereignisse auftreten können: das Ereignis „Erfolg“ mit einer Wahrscheinlichkeit P oder das Ereignis „Misserfolg“ mit der Wahrscheinlichkeit Q =1-p (das sogenannte Bernoulli-Schema,BernoulliVersuche).
Wahrscheinlichkeit, genau zu bekommen X Erfolg in diesen N Tests ist gleich:
Anzahl der Erfolge in der Stichprobe X ist eine Zufallsvariable, die hat Binomialverteilung(Englisch) BinomialVerteilung) P Und N– sind Parameter dieser Verteilung.
Denken Sie daran, um sich zu bewerben Bernoulli-Schemata und entsprechend Binomialverteilung, folgende Bedingungen müssen erfüllt sein:
- Jeder Versuch muss genau zwei Ergebnisse haben, die bedingt als „Erfolg“ und „Misserfolg“ bezeichnet werden.
- Das Ergebnis jedes Tests sollte nicht von den Ergebnissen früherer Tests abhängen (Testunabhängigkeit).
- Erfolgsrate P sollte für alle Tests konstant sein.
Binomialverteilung in MS EXCEL
In MS Excel, ab Version 2010, z Binomialverteilung Es gibt eine Funktion BINOM.DIST() , englischer Name- BINOM.DIST(), mit dem Sie die Wahrscheinlichkeit berechnen können, dass die Stichprobe genau sein wird X„Erfolge“ (d. h. Wahrscheinlichkeitsdichtefunktion p(x), siehe Formel oben), und integrale Verteilungsfunktion(Wahrscheinlichkeit, die die Probe haben wird X oder weniger „Erfolge“, einschließlich 0).
Vor MS EXCEL 2010 verfügte EXCEL über die Funktion BINOMVERT(), mit der Sie auch Berechnungen durchführen können Verteilungsfunktion Und Wahrscheinlichkeitsdichte p(x). BINOMDIST() wird aus Kompatibilitätsgründen in MS EXCEL 2010 belassen.
Die Beispieldatei enthält Diagramme Wahrscheinlichkeitsverteilungsdichte Und .

Binomialverteilung hat die Bezeichnung B(N; P) .
Notiz: Zum Bauen integrale Verteilungsfunktion perfekt passender Diagrammtyp Zeitplan, Für Verteilungsdichte – Histogramm mit Gruppierung. Weitere Informationen zum Erstellen von Diagrammen finden Sie im Artikel Die wichtigsten Diagrammtypen.
Notiz: Um das Schreiben von Formeln in der Beispieldatei zu erleichtern, wurden Namen für Parameter erstellt Binomialverteilung: n und p.

Die Beispieldatei zeigt verschiedene Wahrscheinlichkeitsberechnungen mit MS-EXCEL-Funktionen:

Wie im Bild oben zu sehen ist, wird davon ausgegangen, dass:
- Die unendliche Population, aus der die Stichprobe besteht, enthält 10 % (oder 0,1) gute Elemente (Parameter P, drittes Funktionsargument =BINOM.DIST() )
- Um die Wahrscheinlichkeit zu berechnen, dass in einer Stichprobe von 10 Elementen (Parameter N, das zweite Argument der Funktion) gibt es genau 5 gültige Elemente (das erste Argument), müssen Sie die Formel schreiben: =BINOM.VERT(5, 10, 0,1, FALSCH)
- Das letzte, vierte Element ist gesetzt = FALSE, d.h. Funktionswert wird zurückgegeben Verteilungsdichte.
Wenn der Wert des vierten Arguments = TRUE ist, gibt die Funktion BINOM.DIST() den Wert zurück integrale Verteilungsfunktion oder einfach Verteilungsfunktion. In diesem Fall können Sie die Wahrscheinlichkeit berechnen, dass die Anzahl der guten Elemente in der Stichprobe in einem bestimmten Bereich liegt, beispielsweise 2 oder weniger (einschließlich 0).
Dazu müssen Sie die Formel schreiben:
= BINOM.VERT(2, 10, 0,1, TRUE)
Notiz: Für einen nicht ganzzahligen Wert von x, . Die folgenden Formeln geben beispielsweise denselben Wert zurück:
=BINOM.VERT( 2
; 10; 0,1; WAHR)
=BINOM.VERT( 2,9
; 10; 0,1; WAHR)
Notiz: In der Beispieldatei Wahrscheinlichkeitsdichte Und Verteilungsfunktion wird auch mithilfe der Definition und der Funktion COMBIN() berechnet.
Verteilungsindikatoren
IN Beispieldatei auf Blatt Beispiel Es gibt Formeln zur Berechnung einiger Verteilungsindikatoren:
- =n*p;
- (quadratische Standardabweichung) = n*p*(1-p);
- = (n+1)*p;
- =(1-2*p)*ROOT(n*p*(1-p)).
Wir leiten die Formel ab mathematische Erwartung Binomialverteilung verwenden Bernoulli-Schema.
Per Definition ist eine Zufallsvariable X in Bernoulli-Schema(Bernoulli-Zufallsvariable) hat Verteilungsfunktion:

Diese Verteilung heißt Bernoulli-Verteilung.
Notiz: Bernoulli-Verteilung- besonderer Fall Binomialverteilung mit Parameter n=1.
Lassen Sie uns 3 Arrays mit 100 Zahlen mit unterschiedlichen Erfolgswahrscheinlichkeiten generieren: 0,1; 0,5 und 0,9. Dazu im Fenster Zufallszahlengenerierung Legen Sie für jede Wahrscheinlichkeit p die folgenden Parameter fest:

Notiz: Wenn Sie die Option festlegen Zufällige Streuung (Zufälliger Samen), dann können Sie einen bestimmten zufälligen Satz generierter Zahlen auswählen. Wenn Sie diese Option beispielsweise auf =25 setzen, können Sie dieselben Sätze von Zufallszahlen auf verschiedenen Computern generieren (sofern natürlich andere Verteilungsparameter gleich sind). Der Optionswert kann ganzzahlige Werte von 1 bis 32.767 annehmen. Optionsname Zufällige Streuung kann verwirren. Es wäre besser, es als zu übersetzen Zahl mit Zufallszahlen festlegen.
Als Ergebnis erhalten wir 3 Spalten mit 100 Zahlen, anhand derer wir beispielsweise die Erfolgswahrscheinlichkeit abschätzen können P nach der Formel: Anzahl der Erfolge/100(cm. Beispieldateiblatt Generieren von Bernoulli).

Notiz: Für Bernoulli-Verteilungen mit p=0,5 können Sie die Formel =RANDBETWEEN(0;1) verwenden, die entspricht.
Zufallszahlengenerierung. Binomialverteilung
Angenommen, die Stichprobe enthält 7 fehlerhafte Artikel. Das bedeutet, dass es „sehr wahrscheinlich“ ist, dass sich der Anteil fehlerhafter Produkte verändert hat. P, was ein Merkmal unseres Produktionsprozesses ist. Obwohl diese Situation „sehr wahrscheinlich“ ist, besteht die Möglichkeit (Alpha-Risiko, Typ-1-Fehler, „Fehlalarm“) P blieb unverändert, und die erhöhte Anzahl fehlerhafter Produkte war auf Stichproben zurückzuführen.
Wie in der Abbildung unten zu sehen ist, ist 7 die Anzahl fehlerhafter Produkte, die für einen Prozess mit p=0,21 bei gleichem Wert akzeptabel ist Alpha. Dies verdeutlicht, dass, wenn der Schwellenwert für fehlerhafte Artikel in einer Stichprobe überschritten wird, P„wahrscheinlich“ erhöht. Der Ausdruck „höchstwahrscheinlich“ bedeutet, dass nur eine Wahrscheinlichkeit von 10 % (100 %–90 %) besteht, dass die Abweichung des Prozentsatzes fehlerhafter Produkte über dem Schwellenwert nur auf zufällige Ursachen zurückzuführen ist.

Daher kann das Überschreiten der Schwellenwertanzahl fehlerhafter Produkte in der Stichprobe als Signal dafür dienen, dass der Prozess gestört ist und begonnen hat, b zu produzieren Ö höherer Prozentsatz fehlerhafter Produkte.
Notiz: Vor MS EXCEL 2010 verfügte Excel über eine Funktion CRITBINOM() , die BINOM.INV() entspricht. CRITBINOM() bleibt aus Kompatibilitätsgründen in MS EXCEL 2010 und höher erhalten.
Beziehung der Binomialverteilung zu anderen Verteilungen
Wenn der Parameter N Binomialverteilung tendiert zur Unendlichkeit und P geht in diesem Fall gegen 0 Binomialverteilung angenähert werden kann.
Es ist möglich, Bedingungen für die Näherung zu formulieren Poisson-Verteilung Funktioniert gut:
- P<0,1 (je weniger P und mehr N, desto genauer ist die Näherung);
- P>0,9 (bedenkt, dass Q=1- P, Berechnungen müssen in diesem Fall mit durchgeführt werden Q(A X muss durch ersetzt werden N- X). Daher umso weniger Q und mehr N, desto genauer die Näherung).
Bei 0,1<=p<=0,9 и n*p>10 Binomialverteilung angenähert werden kann.
Wiederum, Binomialverteilung kann als gute Näherung dienen, wenn die Populationsgröße N beträgt Hypergeometrische Verteilung viel größer als die Stichprobengröße n (d. h. N>>n oder n/N).<<1).
Weitere Informationen zum Zusammenhang der oben genannten Verteilungen finden Sie im Artikel. Dort werden auch Beispiele für die Approximation aufgeführt und die Bedingungen erläutert, wann und mit welcher Genauigkeit eine Approximation möglich ist.
BERATUNG: Über weitere Distributionen von MS EXCEL können Sie im Artikel nachlesen.
Im Gegensatz zu den Normal- und Gleichverteilungen, die das Verhalten einer Variablen in der Stichprobe der untersuchten Probanden beschreiben, wird die Binomialverteilung für andere Zwecke verwendet. Es dient dazu, die Wahrscheinlichkeit zweier sich gegenseitig ausschließender Ereignisse in einer bestimmten Anzahl unabhängiger Versuche vorherzusagen. Ein klassisches Beispiel für eine Binomialverteilung ist der Wurf einer Münze, die auf eine harte Oberfläche fällt. Zwei Ergebnisse (Ereignisse) sind gleich wahrscheinlich: 1) Die Münze fällt „Adler“ (die Wahrscheinlichkeit ist gleich R) oder 2) die Münze fällt „Zahl“ (die Wahrscheinlichkeit ist gleich Q). Wenn kein drittes Ergebnis gegeben ist, dann P = Q= 0,5 und P + Q= 1. Mithilfe der Binomialverteilungsformel können Sie beispielsweise bestimmen, wie hoch die Wahrscheinlichkeit ist, dass bei 50 Versuchen (der Anzahl der Münzwürfe) die letzte Münze beispielsweise 25 Mal mit dem Kopf fällt.
Zur weiteren Begründung führen wir die allgemein akzeptierte Notation ein:
N ist die Gesamtzahl der Beobachtungen;
ich- die Anzahl der Ereignisse (Ergebnisse), die für uns von Interesse sind;
N – ich– Anzahl alternativer Veranstaltungen;
P- empirisch ermittelte (manchmal angenommene) Wahrscheinlichkeit eines für uns interessanten Ereignisses;
Q ist die Wahrscheinlichkeit eines alternativen Ereignisses;
P N ( ich) ist die vorhergesagte Wahrscheinlichkeit des für uns interessanten Ereignisses ich für eine bestimmte Anzahl von Beobachtungen N.
Binomialverteilungsformel:
Bei gleichwahrscheinlichem Ausgang der Ereignisse ( p = q) können Sie die vereinfachte Formel verwenden:
![]() (6.8)
(6.8)
Betrachten wir drei Beispiele, die die Verwendung von Binomialverteilungsformeln in der psychologischen Forschung veranschaulichen.
Beispiel 1
Nehmen Sie an, dass drei Schüler ein Problem mit erhöhter Komplexität lösen. Für jeden von ihnen sind 2 Ergebnisse gleich wahrscheinlich: (+) – Lösung und (-) – Nichtlösung des Problems. Insgesamt sind 8 verschiedene Ergebnisse möglich (2 3 = 8).
Die Wahrscheinlichkeit, dass kein Schüler die Aufgabe bewältigen wird, beträgt 1/8 (Option 8); 1 Schüler wird die Aufgabe lösen: P= 3/8 (Optionen 4, 6, 7); 2 Studenten - P= 3/8 (Optionen 2, 3, 5) und 3 Studenten – P=1/8 (Option 1).
Es gilt die Wahrscheinlichkeit zu ermitteln, dass drei von fünf Studierenden diese Aufgabe erfolgreich bewältigen.
Lösung
Insgesamt mögliche Ergebnisse: 2 5 = 32.
Die Gesamtzahl der Optionen 3(+) und 2(-) beträgt

Daher beträgt die Wahrscheinlichkeit des erwarteten Ergebnisses 10/32 » 0,31.
Beispiel 3
Übung
Bestimmen Sie die Wahrscheinlichkeit, dass 5 Extrovertierte in einer Gruppe von 10 zufällig ausgewählten Probanden gefunden werden.
Lösung
1. Geben Sie die Notation ein: p=q= 0,5; N= 10; ich = 5; P 10 (5) = ?
2. Wir verwenden eine vereinfachte Formel (siehe oben):
Abschluss
Die Wahrscheinlichkeit, dass unter 10 zufällig ausgewählten Probanden 5 Extrovertierte gefunden werden, beträgt 0,246.
Anmerkungen
1. Die Berechnung nach der Formel mit einer ausreichend großen Anzahl von Versuchen ist recht mühsam, daher empfiehlt es sich in diesen Fällen, Binomialverteilungstabellen zu verwenden.
2. In manchen Fällen die Werte P Und Q kann zunächst eingestellt werden, jedoch nicht immer. Sie werden in der Regel auf Basis der Ergebnisse von Vorversuchen (Pilotstudien) berechnet.
3. In einem grafischen Bild (in Koordinaten P n(ich) = F(ich)) Die Binomialverteilung kann verschiedene Formen haben: im Fall p = q die Verteilung ist symmetrisch und ähnelt der Gaußschen Normalverteilung; Die Schiefe der Verteilung ist umso größer, je größer der Unterschied zwischen den Wahrscheinlichkeiten ist P Und Q.
Poisson-Verteilung
Die Poisson-Verteilung ist ein Sonderfall der Binomialverteilung und wird verwendet, wenn die Wahrscheinlichkeit interessanter Ereignisse sehr gering ist. Mit anderen Worten: Diese Verteilung beschreibt die Wahrscheinlichkeit seltener Ereignisse. Die Poisson-Formel kann verwendet werden für P < 0,01 и Q ≥ 0,99.
Die Poisson-Gleichung ist eine Näherungsgleichung und wird durch die folgende Formel beschrieben:
![]() (6.9)
(6.9)
Dabei ist μ das Produkt aus der durchschnittlichen Wahrscheinlichkeit des Ereignisses und der Anzahl der Beobachtungen.
Betrachten Sie als Beispiel den Algorithmus zur Lösung des folgenden Problems.
Die Aufgabe
Mehrere Jahre lang wurde in 21 großen Kliniken in Russland eine Massenuntersuchung von Neugeborenen auf die Erkrankung von Säuglingen mit Down-Krankheit durchgeführt (die Stichprobe betrug durchschnittlich 1000 Neugeborene in jeder Klinik). Folgende Daten wurden empfangen:
Übung
1. Bestimmen Sie die durchschnittliche Wahrscheinlichkeit der Erkrankung (bezogen auf die Anzahl der Neugeborenen).
2. Bestimmen Sie die durchschnittliche Anzahl der Neugeborenen mit einer Krankheit.
3. Bestimmen Sie die Wahrscheinlichkeit, dass unter 100 zufällig ausgewählten Neugeborenen 2 Babys mit Down-Krankheit sein werden.
Lösung
1. Bestimmen Sie die durchschnittliche Wahrscheinlichkeit der Erkrankung. Dabei müssen wir uns von der folgenden Überlegung leiten lassen. Morbus Down wurde nur in 10 von 21 Kliniken registriert. In 11 Kliniken wurden keine Erkrankungen festgestellt, in 6 Kliniken wurde 1 Fall registriert, in 2 Kliniken 2 Fälle, in der 1. Klinik 3 und in der 1. Klinik 4 Fälle. 5 Fälle wurden in keiner Klinik gefunden. Um die durchschnittliche Erkrankungswahrscheinlichkeit zu ermitteln, ist es notwendig, die Gesamtzahl der Fälle (6 1 + 2 2 + 1 3 + 1 4 = 17) durch die Gesamtzahl der Neugeborenen (21000) zu dividieren:
![]()
2. Die Anzahl der Neugeborenen, die für eine Krankheit verantwortlich sind, ist der Kehrwert der durchschnittlichen Wahrscheinlichkeit, d. h. gleich der Gesamtzahl der Neugeborenen dividiert durch die Anzahl der registrierten Fälle:
![]()
3. Ersetzen Sie die Werte P = 0,00081, N= 100 und ich= 2 in die Poisson-Formel:
Antworten
Die Wahrscheinlichkeit, dass unter 100 zufällig ausgewählten Neugeborenen zwei Säuglinge mit Morbus Down gefunden werden, beträgt 0,003 (0,3 %).
Verwandte Aufgaben
Aufgabe 6.1
Übung
Berechnen Sie anhand der Daten aus Aufgabe 5.1 zum Zeitpunkt der sensomotorischen Reaktion die Asymmetrie und Kurtosis der Verteilung von VR.
Aufgabe 6. 2
200 Doktoranden wurden auf ihr Intelligenzniveau getestet ( IQ). Nach der Normalisierung der resultierenden Verteilung IQ entsprechend der Standardabweichung wurden folgende Ergebnisse erhalten:
Übung
Bestimmen Sie mithilfe der Kolmogorov- und Chi-Quadrat-Tests, ob die resultierende Verteilung der Indikatoren entspricht IQ normal.
Aufgabe 6. 3
Bei einem erwachsenen Probanden (einem 25-jährigen Mann) wurde die Zeit einer einfachen sensomotorischen Reaktion (SR) als Reaktion auf einen Schallreiz mit einer konstanten Frequenz von 1 kHz und einer Intensität von 40 dB untersucht. Der Reiz wurde hundertmal im Abstand von 3–5 Sekunden präsentiert. Einzelne VR-Werte für 100 Wiederholungen verteilten sich wie folgt:
Übung
1. Erstellen Sie ein Häufigkeitshistogramm der VR-Verteilung; Bestimmen Sie den Durchschnittswert von VR und den Wert der Standardabweichung.
2. Berechnen Sie den Asymmetriekoeffizienten und die Kurtosis der Blutdruckverteilung. basierend auf empfangenen Werten Als Und Ex Machen Sie eine Schlussfolgerung über die Konformität oder Nichtübereinstimmung dieser Verteilung mit der Normalverteilung.
Aufgabe 6.4
Im Jahr 1998 schlossen 14 Personen (5 Jungen und 9 Mädchen) die Schulen in Nischni Tagil mit Goldmedaillen ab, 26 Personen (8 Jungen und 18 Mädchen) mit Silbermedaillen.
Frage
Kann man sagen, dass Mädchen häufiger Medaillen bekommen als Jungen?
Notiz
Das Verhältnis der Anzahl von Jungen und Mädchen in der Gesamtbevölkerung wird als gleich angesehen.
Aufgabe 6.5
Es wird angenommen, dass die Anzahl der Extrovertierten und Introvertierten in einer homogenen Probandengruppe ungefähr gleich ist.
Übung
Bestimmen Sie die Wahrscheinlichkeit, dass in einer Gruppe von 10 zufällig ausgewählten Probanden 0, 1, 2, ..., 10 Extrovertierte gefunden werden. Konstruieren Sie einen grafischen Ausdruck für die Wahrscheinlichkeitsverteilung, 0, 1, 2, ..., 10 Extrovertierte in einer bestimmten Gruppe zu finden.
Aufgabe 6.6
Übung
Berechnen Sie die Wahrscheinlichkeit P n(i) Binomialverteilungsfunktionen für P= 0,3 und Q= 0,7 für Werte N= 5 und ich= 0, 1, 2, ..., 5. Konstruieren Sie einen grafischen Ausdruck der Abhängigkeit P n(ich) = f(ich) .
Aufgabe 6.7
In den letzten Jahren hat sich bei einem Teil der Bevölkerung der Glaube an astrologische Vorhersagen etabliert. Nach den Ergebnissen vorläufiger Umfragen wurde festgestellt, dass etwa 15 % der Bevölkerung an Astrologie glauben.
Übung
Bestimmen Sie die Wahrscheinlichkeit, dass unter 10 zufällig ausgewählten Befragten 1, 2 oder 3 Personen an astrologische Vorhersagen glauben.
Aufgabe 6.8
Die Aufgabe
In 42 weiterführenden Schulen in der Stadt Jekaterinburg und der Region Swerdlowsk (die Gesamtzahl der Schüler beträgt 12.260) wurde über mehrere Jahre hinweg folgende Zahl von Fällen psychischer Erkrankungen bei Schülern festgestellt:
Übung
Lassen Sie 1000 Schüler stichprobenartig untersuchen. Berechnen Sie, wie hoch die Wahrscheinlichkeit ist, dass unter diesen tausend Schulkindern 1, 2 oder 3 psychisch kranke Kinder identifiziert werden?
ABSCHNITT 7. UNTERSCHIEDLICHE MAßE
Formulierung des Problems
Angenommen, wir haben zwei unabhängige Stichproben von Probanden X Und bei. Unabhängig Proben werden gezählt, wenn dasselbe Subjekt (Subjekt) in nur einer Probe vorkommt. Die Aufgabe besteht darin, diese Stichproben (zwei Variablensätze) hinsichtlich ihrer Unterschiede miteinander zu vergleichen. Unabhängig davon, wie nahe die Werte der Variablen in der ersten und zweiten Stichprobe liegen, werden natürlich einige, wenn auch unbedeutende Unterschiede zwischen ihnen festgestellt. Aus Sicht der mathematischen Statistik interessiert uns die Frage, ob die Unterschiede zwischen diesen Stichproben statistisch signifikant (statistisch signifikant) oder unzuverlässig (zufällig) sind.
Die gebräuchlichsten Kriterien für die Signifikanz von Unterschieden zwischen Stichproben sind parametrische Differenzmaße – Kriterium des Schülers Und Fisher-Kriterium. In einigen Fällen werden nichtparametrische Kriterien verwendet - Rosenbaums Q-Test, Mann-Whitney U-Test und andere. Fisher-Winkeltransformation φ*, mit denen Sie als Prozentsätze (Prozentsätze) ausgedrückte Werte miteinander vergleichen können. Und schließlich können als Sonderfall zum Vergleich von Stichproben Kriterien verwendet werden, die die Form von Stichprobenverteilungen charakterisieren – Kriterium χ 2 Pearson Und Kriterium λ Kolmogorov – Smirnov.
Um dieses Thema besser zu verstehen, gehen wir wie folgt vor. Wir werden das gleiche Problem mit vier Methoden lösen, die vier verschiedene Kriterien verwenden – Rosenbaum, Mann-Whitney, Student und Fisher.
Die Aufgabe
30 Schüler (14 Jungen und 16 Mädchen) wurden während der Prüfungssitzung nach dem Spielberger-Test auf den Grad der reaktiven Angst getestet. Folgende Ergebnisse wurden erzielt (Tabelle 7.1):
Tabelle 7.1
| Fächer | Reaktives Angstniveau | |||||||||||||||
| Jugendliche | ||||||||||||||||
| Mädchen |
Übung
Es sollte festgestellt werden, ob die Unterschiede im Ausmaß der reaktiven Angst bei Jungen und Mädchen statistisch signifikant sind.
Die Aufgabenstellung scheint durchaus typisch für einen Psychologen mit Schwerpunkt Pädagogische Psychologie zu sein: Wer erlebt Prüfungsstress stärker – Jungen oder Mädchen? Wenn die Unterschiede zwischen den Stichproben statistisch signifikant sind, dann gibt es in diesem Aspekt erhebliche geschlechtsspezifische Unterschiede; Wenn die Unterschiede zufällig (nicht statistisch signifikant) sind, sollte diese Annahme verworfen werden.
7. 2. Nichtparametrischer Test Q Rosenbaum
Q-Rozenbaums Kriterium basiert auf dem Vergleich von einander „überlagerten“ Reihen von Werten zweier unabhängiger Variablen. Gleichzeitig wird die Art der Verteilung des Merkmals innerhalb jeder Zeile nicht analysiert – in diesem Fall ist nur die Breite der nicht überlappenden Abschnitte der beiden Rangreihen von Bedeutung. Beim Vergleich zweier Rangreihen von Variablen miteinander sind 3 Möglichkeiten möglich:
1. Ranglistenplätze X Und j keinen Überlappungsbereich haben, d. h. alle Werte der ersten Rangfolge ( X) ist größer als alle Werte der zweitrangigen Reihe( j):
In diesem Fall sind die durch ein beliebiges statistisches Kriterium ermittelten Unterschiede zwischen den Stichproben sicherlich signifikant und die Verwendung des Rosenbaum-Kriteriums ist nicht erforderlich. In der Praxis ist diese Option jedoch äußerst selten.
2. Rangreihen überlappen sich vollständig (in der Regel liegt eine der Reihen innerhalb der anderen), es gibt keine nicht überlappenden Zonen. In diesem Fall ist das Rosenbaum-Kriterium nicht anwendbar.

3. Es gibt einen überlappenden Bereich der Reihen sowie zwei nicht überlappende Bereiche ( N 1 Und N 2) bezüglich anders Rangreihe (wir bezeichnen X- eine Reihe nach groß verschoben, j- in Richtung niedrigerer Werte):

Dieser Fall ist typisch für die Anwendung des Rosenbaum-Kriteriums, bei dessen Anwendung folgende Bedingungen zu beachten sind:
1. Das Volumen jeder Probe muss mindestens 11 betragen.
2. Die Stichprobengrößen sollten sich nicht wesentlich voneinander unterscheiden.
Kriterium Q Rosenbaum entspricht der Anzahl der nicht überlappenden Werte: Q = N 1 +N 2 . Die Schlussfolgerung über die Zuverlässigkeit der Unterschiede zwischen den Stichproben wird gezogen, wenn Q > Q kr . Gleichzeitig sind die Werte Q cr sind in speziellen Tabellen (siehe Anhang, Tabelle VIII).
Kehren wir zu unserer Aufgabe zurück. Lassen Sie uns die Notation einführen: X- eine Auswahl an Mädchen, j- Eine Auswahl von Jungen. Für jede Stichprobe erstellen wir eine Rangfolgereihe:
X: 28 30 34 34 35 36 37 39 40 41 42 42 43 44 45 46
j: 26 28 32 32 33 34 35 38 39 40 41 42 43 44
Wir zählen die Anzahl der Werte in nicht überlappenden Bereichen der Rangfolge. In einer Reihe X die Werte 45 und 46 überschneiden sich nicht, d.h. N 1 = 2;in einer Reihe j nur 1 nicht überlappender Wert 26 d.h. N 2 = 1. Daher gilt: Q = N 1 +N 2 = 1 + 2 = 3.
In der Tabelle. VIII Anhang finden wir das Q kr . = 7 (für ein Signifikanzniveau von 0,95) und Q cr = 9 (für ein Signifikanzniveau von 0,99).
Abschluss
Weil das Q<Q cr, dann sind nach dem Rosenbaum-Kriterium die Unterschiede zwischen den Stichproben statistisch nicht signifikant.
Notiz
Der Rosenbaum-Test kann unabhängig von der Art der Verteilung der Variablen verwendet werden, d. h. in diesem Fall ist es nicht erforderlich, die Tests χ 2 von Pearson und λ von Kolmogorov zu verwenden, um die Art der Verteilungen in beiden Stichproben zu bestimmen.
7. 3. U-Mann-Whitney-Test
Im Gegensatz zum Rosenbaum-Kriterium U Der Mann-Whitney-Test basiert auf der Bestimmung der Überlappungszone zwischen zwei Rangreihen, d. h. je kleiner die Überlappungszone, desto signifikanter sind die Unterschiede zwischen den Stichproben. Hierzu wird ein spezielles Verfahren zur Umwandlung von Intervallskalen in Rangskalen verwendet.
Betrachten wir den Berechnungsalgorithmus für U-Kriterium am Beispiel der vorherigen Aufgabe.
Tabelle 7.2
| x, y | R xy | R xy * | R X | R j |
| 26 28 32 32 33 34 35 38 39 40 41 42 43 44 | 2,5 2,5 5,5 5,5 11,5 11,5 16,5 16,5 18,5 18,5 20,5 20,5 25,5 25,5 27,5 27,5 | 2,5 11,5 16,5 18,5 20,5 25,5 27,5 | 1 2,5 5,5 5,5 7 9 11,5 15 16,5 18,5 20,5 23 25,5 27,5 | |
| Σ | 276,5 | 188,5 |
1. Wir erstellen eine einzelne Rangfolgereihe aus zwei unabhängigen Stichproben. In diesem Fall sind die Werte für beide Stichproben gemischt, Spalte 1 ( X, j). Um die weitere Arbeit (auch in der Computerversion) zu vereinfachen, sollten die Werte für verschiedene Proben in unterschiedlichen Schriftarten (oder unterschiedlichen Farben) markiert werden, wobei zu berücksichtigen ist, dass wir sie künftig in unterschiedlichen Spalten veröffentlichen werden.
2. Transformieren Sie die Intervallskala der Werte in eine Ordinalskala (dazu benennen wir alle Werte mit Rangzahlen von 1 bis 30 um, Spalte 2 ( R xy)).
3. Wir führen Korrekturen für verwandte Ränge ein (die gleichen Werte der Variablen werden durch den gleichen Rang bezeichnet, vorausgesetzt, dass sich die Summe der Ränge nicht ändert, Spalte 3 ( R xy *). Zu diesem Zeitpunkt wird empfohlen, die Summen der Ränge in der 2. und 3. Spalte zu berechnen (wenn alle Korrekturen korrekt sind, sollten diese Summen gleich sein).
4. Wir verteilen die Rangzahlen entsprechend ihrer Zugehörigkeit zu einer bestimmten Stichprobe (Spalten 4 und 5 ( R x und R y)).
5. Wir führen Berechnungen nach der Formel durch:
![]() (7.1)
(7.1)
Wo T x ist die größte der Rangsummen ; N x und N y bzw. die Stichprobengrößen. Bedenken Sie in diesem Fall, dass wenn T X< T y , dann die Notation X Und j sollte umgekehrt werden.
6. Vergleichen Sie den erhaltenen Wert mit dem Tabellenwert (siehe Anhänge, Tabelle IX). Die Schlussfolgerung über die Zuverlässigkeit der Unterschiede zwischen den beiden Proben wird gezogen, wenn U exp.< U cr. .
In unserem Beispiel ![]() U exp. = 83,5 > U cr. = 71.
U exp. = 83,5 > U cr. = 71.
Abschluss
Unterschiede zwischen den beiden Stichproben nach dem Mann-Whitney-Test sind statistisch nicht signifikant.
Anmerkungen
1. Der Mann-Whitney-Test unterliegt praktisch keinen Einschränkungen; Die Mindestgrößen der verglichenen Stichproben betragen 2 und 5 Personen (siehe Tabelle IX im Anhang).
2. Ähnlich wie der Rosenbaum-Test kann der Mann-Whitney-Test für jede Stichprobe verwendet werden, unabhängig von der Art der Verteilung.
Kriterium des Schülers
Im Gegensatz zu den Rosenbaum- und Mann-Whitney-Kriterien ist das Kriterium T Die Studentenmethode ist parametrisch, d. h. basiert auf der Bestimmung der wichtigsten statistischen Indikatoren – der Durchschnittswerte in jeder Stichprobe ( und ) und ihrer Varianzen (s 2 x und s 2 y), berechnet mit Standardformeln (siehe Abschnitt 5).
Die Verwendung des Student-Kriteriums impliziert die folgenden Bedingungen:
1. Die Werteverteilungen für beide Stichproben müssen gesetzeskonform sein Normalverteilung(siehe Abschnitt 6).
2. Das Gesamtvolumen der Proben muss mindestens 30 (für β 1 = 0,95) und mindestens 100 (für β 2 = 0,99) betragen.
3. Die Volumina zweier Proben sollten sich nicht wesentlich voneinander unterscheiden (nicht mehr als das 1,5-2-fache).
Die Idee des Student-Kriteriums ist recht einfach. Nehmen wir an, dass die Werte der Variablen in jeder der Stichproben nach dem Normalgesetz verteilt sind, das heißt, wir haben es mit zwei Normalverteilungen zu tun, die sich in Mittelwerten und Varianz (bzw. und) voneinander unterscheiden , und , siehe Abb. 7.1).

S X S j
Reis. 7.1. Schätzung der Unterschiede zwischen zwei unabhängigen Stichproben: und – Mittelwerte der Stichproben X Und j; s x und s y - Standardabweichungen
Es ist leicht zu verstehen, dass die Unterschiede zwischen zwei Stichproben umso größer sind, je größer die Differenz zwischen den Mittelwerten und je kleiner ihre Varianzen (oder Standardabweichungen) sind.
Bei unabhängigen Stichproben wird der Student-Koeffizient durch die Formel bestimmt:
 (7.2)
(7.2)
Wo N x und N y - bzw. die Anzahl der Proben X Und j.
Nach der Berechnung des Student-Koeffizienten in der Tabelle der Standardwerte (kritischen Werte). T(siehe Anhang, Tabelle X) Finden Sie den Wert, der der Anzahl der Freiheitsgrade entspricht n = n x + N y - 2, und vergleichen Sie es mit dem durch die Formel berechneten Wert. Wenn T exp. £ T cr. , dann wird die Hypothese über die Zuverlässigkeit der Unterschiede zwischen den Stichproben abgelehnt, wenn T exp. > T cr. , dann wird es akzeptiert. Mit anderen Worten: Die Stichproben unterscheiden sich signifikant voneinander, wenn der anhand der Formel berechnete Student-Koeffizient größer ist als der Tabellenwert für das entsprechende Signifikanzniveau.
Bei dem Problem, das wir zuvor betrachtet haben, ergibt die Berechnung von Durchschnittswerten und Varianzen die folgenden Werte: X vgl. = 38,5; σ x 2 = 28,40; bei vgl. = 36,2; σ y 2 = 31,72.
Es zeigt sich, dass der durchschnittliche Angstwert in der Gruppe der Mädchen höher ist als in der Gruppe der Jungen. Allerdings sind diese Unterschiede so gering, dass sie wahrscheinlich nicht statistisch signifikant sind. Die Streuung der Werte ist bei Jungen hingegen etwas höher als bei Mädchen, allerdings sind auch die Unterschiede zwischen den Varianzen gering.

Abschluss
T exp. = 1,14< T cr. = 2,05 (β 1 = 0,95). Die Unterschiede zwischen den beiden verglichenen Stichproben sind statistisch nicht signifikant. Diese Schlussfolgerung stimmt weitgehend mit der Schlussfolgerung überein, die anhand der Rosenbaum- und Mann-Whitney-Kriterien gewonnen wurde.
Eine andere Möglichkeit, die Unterschiede zwischen zwei Stichproben mithilfe des Student-t-Tests zu bestimmen, besteht darin, das Konfidenzintervall der Standardabweichungen zu berechnen. Das Konfidenzintervall ist die mittlere quadratische (Standard-)Abweichung dividiert durch die Quadratwurzel der Stichprobengröße und multipliziert mit dem Standardwert des Student-Koeffizienten für N– 1 Freiheitsgrade (bzw. und ).
Notiz
Wert = mx wird als quadratischer Mittelwertfehler bezeichnet (siehe Abschnitt 5). Daher ist das Konfidenzintervall der Standardfehler multipliziert mit dem Student-Koeffizienten für eine gegebene Stichprobengröße, wobei die Anzahl der Freiheitsgrade ν = ist N- 1, und für gegebenes Niveau Bedeutung.
Zwei voneinander unabhängige Stichproben gelten als signifikant unterschiedlich, wenn sich die Konfidenzintervalle für diese Stichproben nicht überschneiden. In unserem Fall haben wir 38,5 ± 2,84 für die erste Stichprobe und 36,2 ± 3,38 für die zweite.
Daher zufällige Variationen x i liegen im Bereich 35,66 ¸ 41,34 und Variationen y i- im Bereich 32,82 ¸ 39,58. Auf dieser Grundlage kann festgestellt werden, dass die Unterschiede zwischen den Proben bestehen X Und j statistisch unzuverlässig (Variationsbereiche überschneiden sich). Dabei ist zu beachten, dass die Breite der Überlappungszone in diesem Fall keine Rolle spielt (nur die Tatsache der Überlappung der Konfidenzintervalle ist wichtig).
Die Student-Methode für voneinander abhängige Stichproben (z. B. zum Vergleich der Ergebnisse wiederholter Tests an derselben Stichprobe von Probanden) wird recht selten verwendet, da es für diese Zwecke andere, aussagekräftigere statistische Techniken gibt (siehe Abschnitt 10). Zu diesem Zweck können Sie jedoch in erster Näherung die Student-Formel der folgenden Form verwenden:
 (7.3)
(7.3)
Das erhaltene Ergebnis wird mit dem Tabellenwert für verglichen N– 1 Freiheitsgrade, wo N– Anzahl der Wertepaare X Und j. Die Ergebnisse des Vergleichs werden genauso interpretiert wie bei der Berechnung der Differenzen zwischen zwei unabhängigen Stichproben.
Fisher-Kriterium
Fisher-Kriterium ( F) basiert auf dem gleichen Prinzip wie der Student-t-Test, d. h. er beinhaltet die Berechnung von Mittelwerten und Varianzen in den verglichenen Stichproben. Es wird am häufigsten verwendet, wenn Proben unterschiedlicher Größe (unterschiedlicher Größe) miteinander verglichen werden. Der Fisher-Test ist etwas strenger als der Student-Test und daher vorzuziehen, wenn Zweifel an der Zuverlässigkeit von Unterschieden bestehen (z. B. wenn laut Student-Test die Unterschiede bei Null signifikant und bei der ersten Signifikanz nicht signifikant sind). eben).
Fishers Formel sieht so aus:
 (7.4)
(7.4)
wo und  (7.5, 7.6)
(7.5, 7.6)
In unserem Problem d2= 5,29; σz 2 = 29,94.
Ersetzen Sie die Werte in der Formel: ![]()
In der Tabelle. XI Anwendungen finden wir für das Signifikanzniveau β 1 = 0,95 und ν = N x + N y - 2 = 28 der kritische Wert ist 4,20.
Abschluss
F = 1,32 < F cr.= 4,20. Die Unterschiede zwischen den Stichproben sind statistisch nicht signifikant.
Notiz
Bei der Verwendung des Fisher-Tests müssen die gleichen Bedingungen erfüllt sein wie beim Student-Test (siehe Abschnitt 7.4). Dennoch ist ein Unterschied in der Anzahl der Proben um mehr als das Zweifache zulässig.
Als wir also das gleiche Problem mit vier verschiedenen Methoden unter Verwendung von zwei nichtparametrischen und zwei parametrischen Kriterien lösten, kamen wir zu dem eindeutigen Schluss, dass die Unterschiede zwischen der Gruppe der Mädchen und der Gruppe der Jungen hinsichtlich des Ausmaßes der reaktiven Angst unzuverlässig sind (d. h. , liegen innerhalb einer zufälligen Variation). Es kann jedoch Fälle geben, in denen eine eindeutige Schlussfolgerung nicht möglich ist: Einige Kriterien ergeben zuverlässige, andere unzuverlässige Unterschiede. In diesen Fällen haben parametrische Kriterien Vorrang (vorbehaltlich der ausreichenden Stichprobengröße und der Normalverteilung der untersuchten Werte).
7. 6. Kriterium j* – Fishers Winkeltransformation
Das j*Fisher-Kriterium dient dazu, zwei Stichproben anhand der Häufigkeit des Auftretens des für den Forscher interessanten Effekts zu vergleichen. Es bewertet die Signifikanz von Unterschieden zwischen den Prozentsätzen zweier Proben, in denen der interessierende Effekt registriert wird. Ein Vergleich von Prozentsätzen innerhalb derselben Stichprobe ist ebenfalls zulässig.
Wesen Winkeltransformation Fisher soll Prozentsätze in Zentralwinkel umrechnen, die im Bogenmaß gemessen werden. Ein größerer Prozentsatz entspricht einem größeren Winkel J und ein kleinerer Anteil – ein kleinerer Winkel, aber die Beziehung ist hier nichtlinear:
![]()
Wo R– Prozentsatz, ausgedrückt in Bruchteilen einer Einheit.
Mit zunehmender Diskrepanz zwischen den Winkeln j 1 und j 2 und einer Zunahme der Anzahl der Stichproben steigt der Wert des Kriteriums.
Das Fisher-Kriterium wird nach folgender Formel berechnet:
| |
wobei j 1 der Winkel ist, der dem größeren Prozentsatz entspricht; j 2 - der Winkel, der einem kleineren Prozentsatz entspricht; N 1 und N 2 - jeweils das Volumen der ersten und zweiten Probe.
Der durch die Formel berechnete Wert wird mit dem Standardwert (j* st = 1,64 für b 1 = 0,95 und j* st = 2,31 für b 2 = 0,99) verglichen. Unterschiede zwischen den beiden Stichproben gelten als statistisch signifikant, wenn j*> j* st für ein gegebenes Signifikanzniveau.
Beispiel
Uns interessiert, ob sich die beiden Studierendengruppen hinsichtlich des Erfolgs bei der Bewältigung einer eher komplexen Aufgabe unterscheiden. In der ersten Gruppe von 20 Personen kamen 12 Schüler damit zurecht, in der zweiten Gruppe 10 von 25 Personen.
Lösung
1. Geben Sie die Notation ein: N 1 = 20, N 2 = 25.
2. Prozentsätze berechnen R 1 und R 2: R 1 = 12 / 20 = 0,6 (60%), R 2 = 10 / 25 = 0,4 (40%).
3. In der Tabelle. XII Anwendungen finden wir die Werte von φ, die Prozentsätzen entsprechen: j 1 = 1,772, j 2 = 1,369.
| |
Von hier:
Abschluss
Unterschiede zwischen Gruppen sind statistisch nicht signifikant, da j*< j* ст для 1-го и тем более для 2-го уровня значимости.
7.7. Verwendung des Pearson-χ2-Tests und des Kolmogorov-λ-Tests
Natürlich sollte man bei der Berechnung der kumulativen Verteilungsfunktion die erwähnte Beziehung zwischen Binomial- und Betaverteilung verwenden. Diese Methode ist sicherlich besser als die direkte Summierung, wenn n > 10.
In klassischen Lehrbüchern zur Statistik wird zur Ermittlung der Werte der Binomialverteilung häufig die Verwendung von Formeln empfohlen, die auf Grenzwertsätzen basieren (z. B. die Moivre-Laplace-Formel). Es ist darauf hinzuweisen, dass aus rein rechnerischer Sicht Der Wert dieser Theoreme liegt nahe bei Null, insbesondere jetzt, wo auf fast jedem Tisch ein leistungsstarker Computer steht. Der Hauptnachteil der oben genannten Näherungen ist ihre völlig unzureichende Genauigkeit für die für die meisten Anwendungen typischen Werte von n. Ein nicht geringerer Nachteil ist das Fehlen klarer Empfehlungen zur Anwendbarkeit der einen oder anderen Näherung (in Standardtexten werden nur asymptotische Formulierungen angegeben, sie werden nicht von Genauigkeitsschätzungen begleitet und sind daher von geringem Nutzen). Ich würde sagen, dass beide Formeln nur für n gültig sind< 200 и для совсем грубых, ориентировочных расчетов, причем делаемых “вручную” с помощью статистических таблиц. А вот связь между биномиальным распределением и бета-распределением позволяет вычислять биномиальное распределение достаточно экономно.
Ich betrachte hier nicht das Problem, Quantile zu finden: Für diskrete Verteilungen ist es trivial, und bei Problemen, bei denen solche Verteilungen auftreten, ist es in der Regel nicht relevant. Wenn dennoch Quantile benötigt werden, empfehle ich, das Problem so umzuformulieren, dass mit p-Werten (beobachteten Signifikanzen) gearbeitet wird. Hier ein Beispiel: Bei der Implementierung einiger Aufzählungsalgorithmen ist bei jedem Schritt eine Überprüfung erforderlich statistische Hypotheseüber eine binomiale Zufallsvariable. Nach dem klassischen Ansatz ist es bei jedem Schritt erforderlich, die Statistik des Kriteriums zu berechnen und seinen Wert mit der Grenze des kritischen Satzes zu vergleichen. Da der Algorithmus jedoch enumerativ ist, ist es notwendig, die Grenze der kritischen Menge jedes Mal neu zu bestimmen (schließlich ändert sich die Stichprobengröße von Schritt zu Schritt), was den Zeitaufwand unproduktiv erhöht. Moderner Ansatz empfiehlt, die beobachtete Signifikanz zu berechnen und mit ihr zu vergleichen Vertrauensniveau, wodurch die Suche nach Quantilen eingespart wird.
Daher berechnen die folgenden Codes nicht die Umkehrfunktion, sondern die Funktion rev_binomialDF, die die Erfolgswahrscheinlichkeit p in einem einzelnen Versuch anhand der Anzahl n der Versuche, der Anzahl m der darin enthaltenen Erfolge und des Werts y berechnet der Wahrscheinlichkeit, diese m Erfolge zu erzielen. Dabei wird die oben erwähnte Beziehung zwischen Binomial- und Betaverteilung genutzt.
Tatsächlich können Sie mit dieser Funktion die Grenzen von Konfidenzintervallen ermitteln. Angenommen, wir erzielen m Erfolge in n Binomialversuchen. Bekanntlich ist die linke Grenze des zweiseitigen Konfidenzintervalls für den Parameter p mit einem Konfidenzniveau 0, wenn m = 0, und für ist die Lösung der Gleichung  . Ebenso ist die rechte Schranke 1, wenn m = n, und for ist eine Lösung der Gleichung
. Ebenso ist die rechte Schranke 1, wenn m = n, und for ist eine Lösung der Gleichung  . Dies impliziert, dass wir die Gleichung auflösen müssen, um die linke Grenze zu finden
. Dies impliziert, dass wir die Gleichung auflösen müssen, um die linke Grenze zu finden  , und nach dem Richtigen zu suchen – der Gleichung
, und nach dem Richtigen zu suchen – der Gleichung  . Sie werden in den Funktionen binom_leftCI und binom_rightCI gelöst, die jeweils die Ober- und Untergrenzen des zweiseitigen Konfidenzintervalls zurückgeben.
. Sie werden in den Funktionen binom_leftCI und binom_rightCI gelöst, die jeweils die Ober- und Untergrenzen des zweiseitigen Konfidenzintervalls zurückgeben.
Ich möchte darauf hinweisen, dass Sie für ausreichend große n die folgende Näherung verwenden können, wenn keine absolut unglaubliche Genauigkeit erforderlich ist [B.L. van der Waerden, Mathematische Statistik. M: IL, 1960, Kap. 2 Sek. 7]:  , wobei g das Quantil der Normalverteilung ist. Der Wert dieser Näherung besteht darin, dass es sehr einfache Näherungen gibt, mit denen Sie die Quantile der Normalverteilung berechnen können (siehe den Text zur Berechnung der Normalverteilung und den entsprechenden Abschnitt dieser Referenz). In meiner Praxis (hauptsächlich für n > 100) ergab diese Näherung etwa 3-4 Ziffern, was in der Regel völlig ausreicht.
, wobei g das Quantil der Normalverteilung ist. Der Wert dieser Näherung besteht darin, dass es sehr einfache Näherungen gibt, mit denen Sie die Quantile der Normalverteilung berechnen können (siehe den Text zur Berechnung der Normalverteilung und den entsprechenden Abschnitt dieser Referenz). In meiner Praxis (hauptsächlich für n > 100) ergab diese Näherung etwa 3-4 Ziffern, was in der Regel völlig ausreicht.
Für Berechnungen mit den folgenden Codes sind die Dateien betaDF.h, betaDF.cpp (siehe Abschnitt zur Beta-Verteilung) sowie logGamma.h, logGamma.cpp (siehe Anhang A) erforderlich. Sie können sich auch ein Beispiel für die Verwendung von Funktionen ansehen.
binomialDF.h-Datei
| #ifndef __BINOMIAL_H__ #include „betaDF.h“ double binomialDF(doppelte Versuche, doppelte Erfolge, doppeltes p); /* * Es gebe „Versuche“ unabhängiger Beobachtungen * mit jeweils einer Erfolgswahrscheinlichkeit „p“. * Berechnen Sie die Wahrscheinlichkeit B(successes|trials,p), dass die Anzahl * der Erfolge zwischen 0 und „Erfolge“ (einschließlich) liegt. */ double rev_binomialDF(doppelte Versuche, doppelte Erfolge, doppeltes y); /* * Es sei die Wahrscheinlichkeit y von mindestens m Erfolgen * in Versuchen des Bernoulli-Schemas bekannt. Die Funktion ermittelt die Erfolgswahrscheinlichkeit p* in einem einzelnen Versuch. * * Die folgende Beziehung wird in Berechnungen verwendet * * 1 - p = rev_Beta(trials-successes| successes+1, y). */ double binom_leftCI(doppelte Versuche, doppelte Erfolge, doppeltes Level); /* Es gebe „Versuche“ unabhängiger Beobachtungen * mit der Erfolgswahrscheinlichkeit „p“ in jedem * und die Anzahl der Erfolge sei „Erfolge“. * Die linke Grenze des zweiseitigen Konfidenzintervalls * wird mit dem Signifikanzniveauniveau berechnet. */ double binom_rightCI(double n, double successes, double level); /* Es gebe „Versuche“ unabhängiger Beobachtungen * mit der Erfolgswahrscheinlichkeit „p“ in jedem * und die Anzahl der Erfolge sei „Erfolge“. * Die rechte Grenze des zweiseitigen Konfidenzintervalls * wird mit dem Signifikanzniveauniveau berechnet. */ #endif /* Endet #ifndef __BINOMIAL_H__ */ |
binomialDF.cpp-Datei
| /***************************************************** **** **********/ /* Binomialverteilung */ /**************************** **** ***************************/ #include |
Grüße an alle Leser!
Wie Sie wissen, befasst sich die statistische Analyse mit der Erhebung und Verarbeitung realer Daten. Es ist nützlich und oft profitabel, weil. Mit den richtigen Schlussfolgerungen können Sie Fehler und Verluste in der Zukunft vermeiden und manchmal genau diese Zukunft richtig einschätzen. Die gesammelten Daten spiegeln den Zustand einiger beobachteter Phänomene wider. Die Daten sind oft (aber nicht immer) numerisch und können mit verschiedenen mathematischen Manipulationen manipuliert werden, um zusätzliche Informationen zu extrahieren.
Allerdings werden nicht alle Phänomene in einer quantitativen Skala wie 1, 2, 3 ... 100500 ... gemessen. Nicht immer kann ein Phänomen unendlich viele oder viele verschiedene Zustände annehmen. Beispielsweise kann das Geschlecht einer Person entweder M oder F sein. Der Schütze trifft entweder das Ziel oder verfehlt es. Sie können entweder „Dafür“ oder „Dagegen“ usw. stimmen. usw. Mit anderen Worten: Solche Daten spiegeln den Status eines alternativen Attributs wider – entweder „Ja“ (das Ereignis ist eingetreten) oder „Nein“ (das Ereignis ist nicht eingetreten). Das kommende Ereignis (positiver Ausgang) wird auch „Erfolg“ genannt. Solche Phänomene können auch massiv und zufällig sein. Daher können sie gemessen und statistisch valide Schlussfolgerungen gezogen werden.
Experimente mit solchen Daten werden aufgerufen Bernoulli-Schema, zu Ehren des berühmten Schweizer Mathematikers, der das damals begründete in großen Zahlen Bei Versuchen bestimmt das Verhältnis der positiven Ergebnisse zur Gesamtzahl der Versuche tendenziell die Wahrscheinlichkeit, dass dieses Ereignis eintritt.
Alternative Feature-Variable
Um den mathematischen Apparat bei der Analyse nutzen zu können, sollten die Ergebnisse solcher Beobachtungen in numerischer Form niedergeschrieben werden. Dazu wird einem positiven Ergebnis die Zahl 1 zugewiesen, einem negativen die Zahl 0. Mit anderen Worten, wir haben es mit einer Variablen zu tun, die nur zwei Werte annehmen kann: 0 oder 1.
Welcher Nutzen lässt sich daraus ziehen? Tatsächlich nicht weniger als aus gewöhnlichen Daten. Daher ist es einfach, die Anzahl der positiven Ergebnisse zu zählen – es reicht aus, alle Werte zusammenzufassen, d. h. alle 1 (Erfolg). Sie können noch weiter gehen, aber dafür müssen Sie ein paar Notationen einführen.
Zunächst ist zu beachten, dass positive Ergebnisse (die gleich 1 sind) mit einer gewissen Wahrscheinlichkeit eintreten. Wenn man beispielsweise bei einem Münzwurf „Kopf“ erhält, beträgt die Quote ½ oder 0,5. Diese Wahrscheinlichkeit wird traditionell mit bezeichnet Lateinischer Buchstabe P. Daher beträgt die Wahrscheinlichkeit für das Eintreten eines alternativen Ereignisses 1-p, was auch mit bezeichnet wird Q, also q = 1 – p. Diese Bezeichnungen können in Form einer variablen Verteilerplatte visuell systematisiert werden X.
Jetzt haben wir eine Liste möglicher Werte und deren Wahrscheinlichkeiten. Sie können mit der Berechnung so wunderbarer Eigenschaften einer Zufallsvariablen beginnen wie erwarteter Wert Und Streuung. Ich möchte Sie daran erinnern, dass der mathematische Erwartungswert als Summe der Produkte aller möglichen Werte und ihrer entsprechenden Wahrscheinlichkeiten berechnet wird:
![]()
Berechnen wir den erwarteten Wert anhand der Notation in den obigen Tabellen.
Es stellt sich heraus, dass die mathematische Erwartung eines alternativen Vorzeichens gleich der Wahrscheinlichkeit dieses Ereignisses ist - P.
Definieren wir nun die Varianz eines alternativen Merkmals. Ich möchte Sie auch daran erinnern, dass die Varianz das mittlere Quadrat der Abweichungen von der mathematischen Erwartung ist. Allgemeine Formel(für diskrete Daten) hat die Form:
Daher die Varianz des Alternativmerkmals:

Es ist leicht zu erkennen, dass diese Streuung maximal 0,25 (at) beträgt p=0,5).
Standardabweichung – Wurzel der Varianz:
Der Maximalwert überschreitet nicht 0,5.
Wie Sie sehen, haben sowohl der mathematische Erwartungswert als auch die Varianz des Alternativzeichens eine sehr kompakte Form.
Binomialverteilung einer Zufallsvariablen
Betrachten Sie die Situation nun aus einem anderen Blickwinkel. Wen interessiert es tatsächlich, dass der durchschnittliche Kopfverlust bei einem Wurf 0,5 beträgt? Es ist sogar unmöglich, es sich vorzustellen. Interessanter ist es, die Frage zu stellen, wie viele Würfe bei einer gegebenen Anzahl von Würfen Kopf ergeben.
Mit anderen Worten: Der Forscher interessiert sich oft für die Wahrscheinlichkeit des Eintretens einer bestimmten Anzahl erfolgreicher Ereignisse. Dies kann die Anzahl fehlerhafter Produkte in der getesteten Charge (1 – fehlerhaft, 0 – gut) oder die Anzahl der Wiederherstellungen (1 – gesund, 0 – krank) usw. sein. Die Anzahl solcher „Erfolge“ entspricht der Summe aller Werte der Variablen X, d.h. die Anzahl der Einzelergebnisse.
Zufälliger Wert B heißt Binomial und nimmt Werte von 0 bis an N(bei B= 0 - alle Teile sind gut, mit B = N- alle Teile sind defekt). Es wird davon ausgegangen, dass alle Werte X unabhängig voneinander. Betrachten Sie die Hauptmerkmale der Binomialvariablen, das heißt, wir werden ihren mathematischen Erwartungswert, ihre Varianz und ihre Verteilung ermitteln.
Der Erwartungswert einer Binomialvariablen ist sehr einfach zu ermitteln. Denken Sie daran, dass es für jeden Mehrwert eine Summe mathematischer Erwartungen gibt, die für alle gleich ist, daher:
Beispielsweise beträgt die Erwartung für die Anzahl der Köpfe bei 100 Würfen 100 × 0,5 = 50.
Nun leiten wir die Formel für die Varianz der Binomialvariablen ab. ist die Summe der Varianzen. Von hier
Standardabweichung bzw
Für 100 Münzwürfe beträgt die Standardabweichung
Und schließlich betrachten wir die Verteilung Binomialwert, d.h. die Wahrscheinlichkeit, dass die Zufallsvariable B werde nehmen verschiedene Bedeutungen k, Wo 0≤k≤n. Bei einer Münze könnte dieses Problem so klingen: Wie groß ist die Wahrscheinlichkeit, bei 100 Würfen 40 Köpfe zu bekommen?
Um die Berechnungsmethode zu verstehen, stellen wir uns vor, dass die Münze nur viermal geworfen wird. Es kann jedes Mal passieren, dass beide Seiten herausfallen. Wir fragen uns: Wie hoch ist die Wahrscheinlichkeit, bei 4 Würfen 2 Köpfe zu bekommen? Jeder Wurf ist unabhängig voneinander. Das bedeutet, dass die Wahrscheinlichkeit, eine beliebige Kombination zu erhalten, dem Produkt der Wahrscheinlichkeiten eines bestimmten Ergebnisses für jeden einzelnen Wurf entspricht. Seien O Kopf und P Zahl. Dann könnte zum Beispiel eine der für uns passenden Kombinationen wie OOPP aussehen, also:

Die Wahrscheinlichkeit einer solchen Kombination ist gleich dem Produkt aus zwei Wahrscheinlichkeiten, dass es „Kopf“ gibt, und zwei weiteren Wahrscheinlichkeiten, dass es kein „Kopf“ gibt (das umgekehrte Ereignis wird wie folgt berechnet). 1-p), d.h. 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Dies ist die Wahrscheinlichkeit einer der Kombinationen, die zu uns passt. Aber es ging um die Gesamtzahl der Adler und nicht um eine bestimmte Reihenfolge. Dann müssen Sie die Wahrscheinlichkeiten aller Kombinationen addieren, in denen es genau 2 Adler gibt. Es ist klar, dass sie alle gleich sind (das Produkt ändert sich nicht, wenn die Orte der Faktoren geändert werden). Daher müssen Sie ihre Anzahl berechnen und sie dann mit der Wahrscheinlichkeit einer solchen Kombination multiplizieren. Zählen wir alle Kombinationen von 4 Würfen mit 2 Adlern: RROO, RORO, ROOR, ORRO, OROR, OORR. Nur 6 Optionen.

Daher beträgt die gewünschte Wahrscheinlichkeit, nach 4 Würfen 2 Köpfe zu bekommen, 6×0,0625=0,375.
Allerdings ist das Zählen auf diese Weise mühsam. Bereits für 10 Münzen wird es sehr schwierig sein, mit roher Gewalt die Gesamtzahl der Optionen zu erhalten. Daher haben kluge Köpfe vor langer Zeit eine Formel erfunden, mit deren Hilfe sie die Anzahl der verschiedenen Kombinationen von berechnen N Elemente von k, Wo N ist die Gesamtzahl der Elemente, k ist die Anzahl der Elemente, deren Anordnungsmöglichkeiten berechnet werden. Kombinationsformel von N Elemente von k Ist:
![]()
Ähnliches geschieht im Bereich der Kombinatorik. Ich schicke jeden dorthin, der sein Wissen verbessern möchte. Daher übrigens auch der Name der Binomialverteilung (die obige Formel ist der Koeffizient bei der Entwicklung des Newton-Binomials).
Die Formel zur Bestimmung der Wahrscheinlichkeit lässt sich leicht auf eine beliebige Zahl verallgemeinern N Und k. Infolgedessen hat die Binomialverteilungsformel die folgende Form.
Mit anderen Worten: Multiplizieren Sie die Anzahl der passenden Kombinationen mit der Wahrscheinlichkeit einer davon.
Für praktischer Nutzen Es reicht aus, nur die Formel der Binomialverteilung zu kennen. Und Sie wissen es vielleicht noch nicht einmal – im Folgenden erfahren Sie, wie Sie die Wahrscheinlichkeit mit Excel ermitteln. Aber es ist besser zu wissen.
Lassen Sie uns diese Formel verwenden, um die Wahrscheinlichkeit zu berechnen, bei 100 Würfen 40 Köpfe zu erzielen:
Oder nur 1,08 %. Zum Vergleich: Die Wahrscheinlichkeit der mathematischen Erwartung dieses Experiments, also 50 Köpfe, beträgt 7,96 %. Die maximale Wahrscheinlichkeit eines Binomialwerts gehört zu dem Wert, der der mathematischen Erwartung entspricht.
Berechnung der Wahrscheinlichkeiten der Binomialverteilung in Excel
Wenn Sie nur Papier und einen Taschenrechner verwenden, erfolgt die Berechnung nach der Formel Binomialverteilung sind trotz des Fehlens von Integralen ziemlich schwierig. Beispielsweise ein Wert von 100! - hat mehr als 150 Zeichen. Eine manuelle Berechnung ist nicht möglich. Früher und heute werden zur Berechnung solcher Größen Näherungsformeln verwendet. Derzeit empfiehlt sich der Einsatz spezieller Software, beispielsweise MS Excel. Somit kann jeder Benutzer (auch ein ausgebildeter Humanist) leicht die Wahrscheinlichkeit des Wertes einer binomialverteilten Zufallsvariablen berechnen.
Zur Konsolidierung des Materials nutzen wir vorerst Excel als regulären Taschenrechner, d.h. Lassen Sie uns eine schrittweise Berechnung mithilfe der Binomialverteilungsformel durchführen. Berechnen wir zum Beispiel die Wahrscheinlichkeit, 50 Köpfe zu bekommen. Unten sehen Sie ein Bild mit den Berechnungsschritten und dem Endergebnis.

Wie Sie sehen, sind die Zwischenergebnisse so groß, dass sie nicht in eine Zelle passen, obwohl überall einfache Funktionen wie FACTOR (Fakultätsrechnung) und POWER (Potenzierung einer Zahl) verwendet werden als Multiplikations- und Divisionsoperatoren. Darüber hinaus ist diese Berechnung ziemlich umständlich, auf jeden Fall ist sie nicht kompakt, da viele Zellen beteiligt. Und ja, es ist schwer, es herauszufinden.
Generell stellt Excel eine vorgefertigte Funktion zur Berechnung der Wahrscheinlichkeiten der Binomialverteilung zur Verfügung. Die Funktion heißt BINOM.VERT.

Anzahl der Erfolge ist die Anzahl der erfolgreichen Versuche. Wir haben 50 davon.
Anzahl von Versuchen- Anzahl der Würfe: 100 Mal.
Erfolgswahrscheinlichkeit– Die Wahrscheinlichkeit, bei einem Wurf „Kopf“ zu bekommen, beträgt 0,5.
Integral- Es wird entweder 1 oder 0 angezeigt. Bei 0 wird die Wahrscheinlichkeit berechnet P(B=k); wenn 1, dann wird die Binomialverteilungsfunktion berechnet, d.h. Summe aller Wahrscheinlichkeiten aus B=0 Vor B=k inklusive.
Wir drücken OK und erhalten das gleiche Ergebnis wie oben, nur dass alles mit einer Funktion berechnet wurde.

Sehr bequem. Aus Versuchsgründen setzen wir statt des letzten Parameters 0 1. Wir erhalten 0,5398. Das bedeutet, dass bei 100 Münzwürfen die Wahrscheinlichkeit, Kopf zwischen 0 und 50 zu bekommen, bei fast 54 % liegt. Und zunächst schien es, als müssten es 50 % sein. Im Allgemeinen sind Berechnungen einfach und schnell durchzuführen.
Ein echter Analyst muss verstehen, wie sich die Funktion verhält (wie ist ihre Verteilung), also berechnen wir die Wahrscheinlichkeiten für alle Werte von 0 bis 100. Das heißt, fragen wir uns: Wie hoch ist die Wahrscheinlichkeit, dass kein einziger Adler fällt? dass 1 Adler fallen wird, 2, 3, 50, 90 oder 100. Die Berechnung ist im folgenden selbstbewegten Bild dargestellt. Die blaue Linie ist die Binomialverteilung selbst, der rote Punkt ist die Wahrscheinlichkeit für eine bestimmte Anzahl an Erfolgen k.

Man könnte fragen, ob die Binomialverteilung nicht ähnlich ist ... Ja, sehr ähnlich. Sogar De Moivre (1733) sagte, dass sich bei großen Stichproben die Binomialverteilung annähert (ich weiß nicht, wie sie damals hieß), aber niemand hörte ihm zu. Erst Gauß und dann 60-70 Jahre später Laplace entdeckten das Normalverteilungsgesetz wieder und untersuchten es sorgfältig. Die obige Grafik zeigt deutlich, dass die maximale Wahrscheinlichkeit auf der mathematischen Erwartung liegt und bei Abweichung davon stark abnimmt. Genau wie das normale Gesetz.
Die Binomialverteilung ist von großer praktischer Bedeutung, sie kommt häufig vor. Mit Hilfe Excel-Berechnungen schnell und unkompliziert durchgeführt. Nutzen Sie es also gerne.
Hiermit schlage ich vor, mich bis zum nächsten Treffen zu verabschieden. Alles Gute, bleiben Sie gesund!




