". Der erste Teil skizziert die zum Verständnis der Chemometrie minimal notwendigen Bestimmungen und der zweite Teil enthält die Fakten, die Sie für ein tieferes Verständnis der Methoden der multivariaten Analyse wissen müssen. Die Präsentation wird durch Beispiele illustriert, die in einem Excel-Arbeitsbuch erstellt wurden Matrix.xls die diesem Dokument beiliegt.

Links zu Beispielen werden als Excel-Objekte im Text platziert. Diese Beispiele sind abstrakter Natur, sie sind in keiner Weise an Aufgaben gebunden. analytische Chemie. Echte Beispiele Die Verwendung der Matrixalgebra in der Chemometrie wird in anderen Texten diskutiert, die sich mit verschiedenen chemometrischen Anwendungen befassen.

Die meisten Messungen, die in der analytischen Chemie durchgeführt werden, sind aber nicht direkt indirekt. Das bedeutet, dass im Experiment anstelle des Werts des gewünschten Analyten C (Konzentration) ein anderer Wert erhalten wird X(Signal) verwandt, aber nicht gleich C, d.h. X(C) ≠ C. In der Regel die Art der Abhängigkeit X(C) ist nicht bekannt, aber glücklicherweise sind in der analytischen Chemie die meisten Messungen proportional. Dies bedeutet, dass als Konzentration von C in A mal erhöht sich das Signal X um den gleichen Betrag, d.h. X(A c) = ein x(C). Außerdem sind die Signale auch additiv, so dass das Signal von einer Probe, die zwei Substanzen mit den Konzentrationen C 1 und C 2 enthält, gleich der Summe der Signale von jeder Komponente sein wird, d. h. X(C1 + C2) = X(C1)+ X(C2). Proportionalität und Additivität ergeben zusammen Linearität. Viele Beispiele können angeführt werden, um das Prinzip der Linearität zu veranschaulichen, aber es genügt, zwei der auffallendsten Beispiele zu nennen – Chromatographie und Spektroskopie. Das zweite Merkmal, das dem Experiment in der analytischen Chemie innewohnt, ist Mehrkanal. Moderne Analysegeräte messen gleichzeitig Signale für viele Kanäle. Beispielsweise wird die Intensität der Lichttransmission für mehrere Wellenlängen gleichzeitig gemessen, d.h. Bereich. Daher haben wir es im Experiment mit einer Vielzahl von Signalen zu tun X 1 , X 2 ,...., X n Charakterisierung der Menge von Konzentrationen C 1 , C 2 , ..., C m von Stoffen, die in dem untersuchten System vorhanden sind.

Reis. 1 Spektren

Das analytische Experiment ist also durch Linearität und Mehrdimensionalität gekennzeichnet. Daher ist es zweckmäßig, experimentelle Daten als Vektoren und Matrizen zu betrachten und sie mit dem Apparat der Matrizenalgebra zu manipulieren. Die Fruchtbarkeit dieses Ansatzes wird durch das in gezeigte Beispiel veranschaulicht, das drei Spektren zeigt, die für 200 Wellenlängen von 4000 bis 4796 cm–1 aufgenommen wurden. Erste ( X 1) und zweitens ( X 2) Die Spektren wurden für Standardproben erhalten, in denen die Konzentrationen von zwei Stoffen A und B bekannt sind: in der ersten Probe [A] = 0,5, [B] = 0,1 und in der zweiten Probe [A] = 0,2, [ B] = 0,6. Was kann man über eine neue, unbekannte Probe sagen, deren Spektrum angegeben ist X 3 ?

Betrachten Sie drei experimentelle Spektren X 1 , X 2 und X 3 als drei Vektoren der Dimension 200. Mit linearer Algebra kann man das leicht zeigen X 3 = 0.1 X 1 +0.3 X 2 , also enthält die dritte Probe offensichtlich nur die Substanzen A und B in den Konzentrationen [A] = 0,5×0,1 + 0,2×0,3 = 0,11 und [B] = 0,1×0,1 + 0,6×0,3 = 0,19.

1. Grundlegende Informationen

1.1 Matrizen

Matrix wird beispielsweise als rechteckige Zahlentabelle bezeichnet

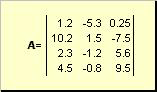
Reis. 2 Matrix

Matrizen werden durch fette Großbuchstaben ( A) und ihre Elemente - mit den entsprechenden Kleinbuchstaben mit Indizes, d.h. A ij . Der erste Index nummeriert die Zeilen und der zweite die Spalten. In der Chemometrie ist es üblich, den Maximalwert des Index mit demselben Buchstaben wie den Index selbst zu bezeichnen, jedoch in Großbuchstaben. Daher die Matrix A kann auch geschrieben werden als ( A ij , ich = 1,..., ICH; J = 1,..., J). Für die Beispielmatrix ICH = 4, J= 3 und A 23 = −7.5.

Zahlenpaar ICH Und J heißt die Dimension der Matrix und wird als bezeichnet ICH× J. Ein Beispiel für eine Matrix in der Chemometrie ist ein Satz von Spektren, die für erhalten wurden ICH Proben an J Wellenlängen.

1.2. Die einfachsten Operationen mit Matrizen

Matrizen können mit Zahlen multiplizieren. In diesem Fall wird jedes Element mit dieser Zahl multipliziert. Zum Beispiel -

Reis. 3 Multiplikation einer Matrix mit einer Zahl

Zwei Matrizen gleicher Dimension können elementweise sein falten Und subtrahieren. Zum Beispiel,

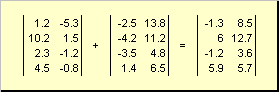
Reis. 4 Matrixaddition

Durch Multiplikation mit einer Zahl und Addition erhält man eine Matrix gleicher Dimension.

Eine Nullmatrix ist eine Matrix, die aus Nullen besteht. Es ist bezeichnet Ö. Es ist klar, dass A+Ö = A, A−A = Ö und 0 A = Ö.

Die Matrix kann transponieren. Während dieser Operation wird die Matrix umgedreht, d.h. Zeilen und Spalten werden vertauscht. Die Transposition wird durch einen Bindestrich angezeigt, A" oder Index A T . Also wenn A = {A ij , ich = 1,..., ICH; J = 1,...,J), Das A t = ( A ji , J = 1,...,J; ich = 1,..., ICH). Zum Beispiel

Reis. 5 Matrixtransposition

Es ist klar, dass ( A t) t = A, (A+B) T = A t+ B T .

1.3. Matrix-Multiplikation

Matrizen können multiplizieren, aber nur, wenn sie die entsprechenden Abmessungen haben. Warum das so ist, wird aus der Definition deutlich. Matrixprodukt A, Abmessungen ICH× K, und Matrizen B, Abmessungen K× J, heißt Matrix C, Abmessungen ICH× J, deren Elemente Zahlen sind

Also für das Produkt AB Es ist notwendig, dass die Anzahl der Spalten in der linken Matrix A war gleich der Anzahl der Zeilen in der rechten Matrix B. Matrix-Produktbeispiel -

Abb.6 Produkt von Matrizen

Die Matrizenmultiplikationsregel kann wie folgt formuliert werden. Um ein Element einer Matrix zu finden C an der Kreuzung stehen ich-te Zeile und J-te Spalte ( C ij) muss elementweise multipliziert werden ich-te Reihe der ersten Matrix A An J-te Spalte der zweiten Matrix B und addiere alle Ergebnisse. Im gezeigten Beispiel ergibt sich also das Element aus der dritten Zeile und der zweiten Spalte als Summe der elementweisen Produkte der dritten Zeile A und zweite Spalte B

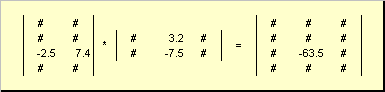
Abb.7 Element des Produkts von Matrizen

Das Produkt von Matrizen hängt von der Reihenfolge ab, d.h. AB ≠ BA, zumindest aus dimensionalen Gründen. Man sagt, es sei nicht kommutativ. Das Produkt von Matrizen ist jedoch assoziativ. Das bedeutet es ABC = (AB)C = A(BC). Außerdem ist es auch distributiv, d.h. A(B+C) = AB+AC. Es ist klar, dass AO = Ö.

1.4. Quadratische Matrizen

Wenn die Anzahl der Spalten einer Matrix gleich der Anzahl ihrer Zeilen ist ( ICH = J=N), dann heißt eine solche Matrix quadratisch. In diesem Abschnitt werden wir nur solche Matrizen betrachten. Unter diesen Matrizen kann man Matrizen mit besonderen Eigenschaften herausgreifen.

Einsam Matrix (bezeichnet ICH und manchmal E) ist eine Matrix, in der alle Elemente gleich Null sind, außer den diagonalen, die gleich 1 sind, d.h.

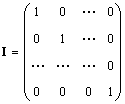
Offensichtlich KI = IA = A.

Die Matrix wird aufgerufen Diagonale, wenn alle seine Elemente außer den diagonalen ( A ii) sind gleich Null. Zum Beispiel

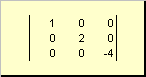
Reis. 8 Diagonalmatrix

Matrix A oben genannt dreieckig, wenn alle unterhalb der Diagonale liegenden Elemente gleich Null sind, d.h. A ij= 0, bei ich>J. Zum Beispiel

Reis. 9 Obere Dreiecksmatrix

Die untere Dreiecksmatrix ist ähnlich definiert.

Matrix A genannt symmetrisch, Wenn A t = A. Mit anderen Worten A ij = A ji. Zum Beispiel

Reis. 10 Symmetrische Matrix

Matrix A genannt senkrecht, Wenn

A T A = AA t = ICH.

Die Matrix wird aufgerufen normal Wenn

1.5. Spur und Determinante

Folgend quadratische Matrix A(bezeichnet mit Tr( A) oder Sp( A)) ist die Summe seiner diagonalen Elemente,

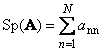
Zum Beispiel,

Reis. 11 Matrixspur

Es ist klar, dass

Sp(α A) = αSp( A) Und

Sp( A+B) = Sp( A)+ Sp( B).

Das lässt sich zeigen

Sp( A) = Sp( A t), Sp( ICH) = N,

und auch das

Sp( AB) = Sp( BA).

Ein weiteres wichtiges Merkmal einer quadratischen Matrix ist ihre bestimmend(bezeichnet durch det( A)). Die Definition der Determinante in Allgemeiner Fall ziemlich kompliziert, also beginnen wir mit der einfachsten Option - der Matrix A Dimension (2×2). Dann

Für eine (3×3)-Matrix ist die Determinante gleich

Bei einer Matrix ( N× N) wird die Determinante als Summe 1 2 3 ... N= N! Begriffe, von denen jeder gleich ist

Indizes k 1 , k 2 ,..., kN sind als alle möglichen geordneten Permutationen definiert R Zahlen in der Menge (1, 2, ... , N). Die Berechnung der Matrixdeterminante ist ein komplexer Vorgang, der in der Praxis mit speziellen Programmen durchgeführt wird. Zum Beispiel,

Reis. 12 Matrixdeterminante

Wir notieren nur die offensichtlichen Eigenschaften:

det( ICH) = 1, det( A) = det( A T),

det( AB) = det( A)det( B).

1.6. Vektoren

Wenn die Matrix nur eine Spalte hat ( J= 1), dann wird ein solches Objekt aufgerufen Vektor. Genauer gesagt ein Spaltenvektor. Zum Beispiel

Denkbar sind beispielsweise auch einzeilige Matrizen

Dieses Objekt ist auch ein Vektor, aber Zeilenvektor. Bei der Analyse von Daten ist es wichtig zu verstehen, mit welchen Vektoren wir es zu tun haben – Spalten oder Zeilen. Das für eine Probe aufgenommene Spektrum kann also als Zeilenvektor betrachtet werden. Dann sollte der Satz von spektralen Intensitäten bei irgendeiner Wellenlänge für alle Proben als Spaltenvektor behandelt werden.

Die Dimension eines Vektors ist die Anzahl seiner Elemente.

Es ist klar, dass jeder Spaltenvektor durch Transposition in einen Zeilenvektor transformiert werden kann, d.h.

In den Fällen, in denen die Form eines Vektors nicht speziell angegeben ist, sondern einfach von einem Vektor gesprochen wird, ist ein Spaltenvektor gemeint. Auch wir werden uns an diese Regel halten. Ein Vektor wird durch einen fetten Kleinbuchstaben gekennzeichnet. Ein Nullvektor ist ein Vektor, dessen Elemente alle gleich Null sind. Es ist bezeichnet 0 .

1.7. Die einfachsten Operationen mit Vektoren

Vektoren können wie Matrizen addiert und mit Zahlen multipliziert werden. Zum Beispiel,

Reis. 13 Operationen mit Vektoren

Zwei Vektoren X Und j genannt kollinear, falls es eine solche Zahl α gibt

1.8. Produkte von Vektoren

Zwei Vektoren derselben Dimension N kann multipliziert werden. Es seien zwei Vektoren X = (X 1 , X 2 ,...,X N) t und j = (j 1 , j 2 ,...,j N) t. Geleitet von der Multiplikationsregel „Zeile für Spalte“ können wir daraus zwei Produkte bilden: X T j Und xy T . Erste Arbeit

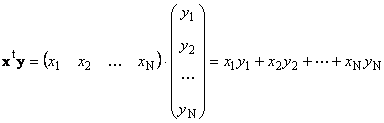
genannt Skalar oder intern. Sein Ergebnis ist eine Zahl. Es verwendet auch die Notation ( X,j)= X T j. Zum Beispiel,

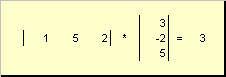
Reis. 14 Inneres (Skalar-)Produkt

Zweites Werk

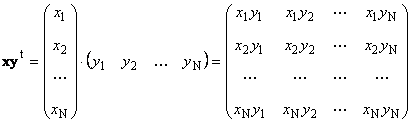
genannt extern. Das Ergebnis ist eine Dimensionsmatrix ( N× N). Zum Beispiel,

Reis. 15 Äußeres Produkt

Man nennt Vektoren, deren Skalarprodukt gleich Null ist senkrecht.

1.9. Vektornorm

Das Skalarprodukt eines Vektors mit sich selbst heißt Skalarquadrat. Dieser Wert

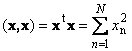
definiert ein Quadrat Länge Vektor X. Zur Bezeichnung der Länge (auch genannt Die Norm Vektor) wird die Notation verwendet

Zum Beispiel,

Reis. 16 Vektornorm

Einheitslängenvektor (|| X|| = 1) heißt normalisiert. Vektor ungleich Null ( X ≠ 0 ) lässt sich normalisieren, indem man sie durch die Länge dividiert, d. h. X = ||X|| (X/||X||) = ||X|| e. Hier e = X/||X|| ist ein normalisierter Vektor.

Vektoren heißen orthonormal, wenn sie alle normalisiert und paarweise orthogonal sind.

1.10. Winkel zwischen Vektoren

Das Skalarprodukt definiert und Eckeφ zwischen zwei Vektoren X Und j

Wenn die Vektoren orthogonal sind, dann ist cosφ = 0 und φ = π/2, und wenn sie kollinear sind, dann ist cosφ = 1 und φ = 0.

1.11. Vektordarstellung einer Matrix

Jede Matrix A Größe ICH× J kann als Menge von Vektoren dargestellt werden

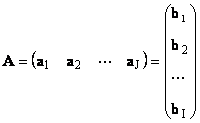
Hier jeder Vektor A J Ist J-ten Spalten- und Zeilenvektor B ich Ist ich-te Zeile der Matrix A

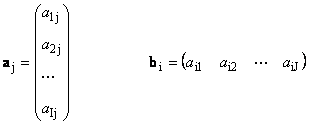
1.12. Linear abhängige Vektoren

Vektoren gleicher Dimension ( N) können wie Matrizen addiert und mit einer Zahl multipliziert werden. Das Ergebnis ist ein Vektor derselben Dimension. Es gebe mehrere Vektoren derselben Dimension X 1 , X 2 ,...,X K und die gleiche Anzahl von Zahlen α α 1 , α 2 ,...,α K. Vektor

j= α1 X 1 + α2 X 2 +...+α K X K

genannt lineare Kombination Vektoren X k .

Wenn es solche Zahlen ungleich Null gibt, ist α k ≠ 0, k = 1,..., K, Was j = 0 , dann eine solche Menge von Vektoren X k genannt linear abhängig. Andernfalls heißen die Vektoren linear unabhängig. Zum Beispiel Vektoren X 1 = (2, 2) t und X 2 = (−1, −1) t sind linear abhängig, da X 1 +2X 2 = 0

1.13. Matrix-Rang

Betrachten Sie eine Reihe von K Vektoren X 1 , X 2 ,...,X K Maße N. Der Rang dieses Vektorsystems ist die maximale Anzahl linear unabhängiger Vektoren. Zum Beispiel im Set

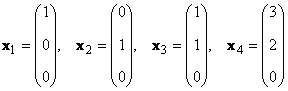
es gibt zum Beispiel nur zwei linear unabhängige Vektoren X 1 und X 2 , also ist sein Rang 2.

Offensichtlich, wenn es mehr Vektoren in der Menge gibt als ihre Dimension ( K>N), dann sind sie zwangsläufig linear abhängig.

Matrix-Rang(bezeichnet durch Rang ( A)) ist der Rang des Vektorsystems, aus dem es besteht. Obwohl jede Matrix auf zwei Arten dargestellt werden kann (Spaltenvektoren oder Zeilenvektoren), hat dies keinen Einfluss auf den Rangwert, da

1.14. inverse Matrix

quadratische Matrix A heißt nicht entartet, wenn es ein Unique hat umkehren Matrix A-1 , bestimmt durch die Bedingungen

AA −1 = A −1 A = ICH.

Die inverse Matrix existiert nicht für alle Matrizen. Eine notwendige und hinreichende Bedingung für Nichtentartung ist

det( A) ≠ 0 oder Rang( A) = N.

Die Matrixinversion ist ein komplexer Vorgang, für den es spezielle Programme gibt. Zum Beispiel,

Reis. 17 Matrixumkehrung

Wir geben Formeln für den einfachsten Fall an - Matrizen 2 × 2

Wenn Matrizen A Und B sind also nicht entartet

(AB) −1 = B −1 A −1 .

1.15. Pseudo-inverse Matrix

Wenn die Matrix A entartet ist und die inverse Matrix nicht existiert, dann kann man in manchen Fällen verwenden pseudo-invers Matrix, die als eine solche Matrix definiert ist A+ das

AA + A = A.

Die pseudoinverse Matrix ist nicht die einzige und ihre Form hängt von der Konstruktionsmethode ab. Für eine rechteckige Matrix können Sie beispielsweise die Moore-Penrose-Methode verwenden.

Wenn die Anzahl der Spalten kleiner als die Anzahl der Zeilen ist, dann

A + =(A T A) −1 A T

Zum Beispiel,

Reis. 17a Pseudo-Matrix-Inversion

Wenn die Anzahl der Spalten größer als die Anzahl der Zeilen ist, dann

A + =A T ( AA T) −1

1.16. Multiplikation eines Vektors mit einer Matrix

Vektor X kann mit einer Matrix multipliziert werden A passendes Maß. In diesem Fall wird der Spaltenvektor rechts multipliziert Axt, und die Vektorzeichenfolge befindet sich auf der linken Seite X T A. Wenn die Dimension des Vektors J, und die Dimension der Matrix ICH× J dann ist das Ergebnis ein Dimensionsvektor ICH. Zum Beispiel,

Reis. 18 Vektor-Matrix-Multiplikation

Wenn die Matrix A- Quadrat ( ICH× ICH), dann der Vektor j = Axt hat die gleichen Maße wie X. Es ist klar, dass

A(α1 X 1 + α2 X 2) = α1 Axt 1 + α2 Axt 2 .

Daher können Matrizen als lineare Transformationen von Vektoren betrachtet werden. Insbesondere X = X, Ochse = 0 .

2. Zusätzliche Informationen

2.1. Systeme linearer Gleichungen

Lassen A- Matrixgröße ICH× J, A B- Dimensionsvektor J. Betrachten Sie die Gleichung

Axt = B

bezüglich des Vektors X, Maße ICH. Im Wesentlichen ist dies ein System von ICH lineare Gleichungen Mit J Unbekannt X 1 ,...,X J. Eine Lösung existiert genau dann, wenn

Rang( A) = Rang ( B) = R,

Wo B ist die erweiterte Dimensionsmatrix ICH×( J+1) bestehend aus der Matrix A, mit einer Spalte aufgefüllt B, B = (A B). Andernfalls sind die Gleichungen inkonsistent.

Wenn R = ICH = J, dann ist die Lösung eindeutig

X = A −1 B.

Wenn R < ICH, dann gibt es viele verschiedene Lösungen, die durch eine Linearkombination ausgedrückt werden können J−R Vektoren. System homogene Gleichungen Axt = 0 mit quadratischer Matrix A (N× N) hat eine nichttriviale Lösung ( X ≠ 0 ) genau dann wenn det( A) = 0. Wenn R= Rang ( A)<N, dann gibt es N−R linear unabhängige Lösungen.

2.2. Bilineare und quadratische Formen

Wenn A ist eine quadratische Matrix, und X Und j- Vektoren der entsprechenden Dimension, dann das Skalarprodukt der Form X T Ja genannt bilinear die durch die Matrix definierte Form A. Bei X = j Ausdruck X T Axt genannt quadratisch form.

2.3. Positiv definite Matrizen

quadratische Matrix A genannt positiv bestimmt, falls für irgendeinen Nicht-Null-Vektor X ≠ 0 ,

X T Axt > 0.

Der Negativ (X T Axt < 0), nicht negativ (X T Axt≥ 0) und nicht positiv (X T Axt≤ 0) bestimmte Matrizen.

2.4. Cholesky-Zerlegung

Wenn die symmetrische Matrix A positiv definit ist, dann gibt es eine eindeutige Dreiecksmatrix U mit positiven Elementen, für die

A = U T U.

Zum Beispiel,

Reis. 19 Cholesky-Zerlegung

2.5. polare Zerlegung

Lassen A ist eine nicht entartete quadratische Dimensionsmatrix N× N. Dann gibt es ein Unikat Polar- Leistung

A = SR,

Wo S eine nicht negative symmetrische Matrix ist, und R ist eine orthogonale Matrix. Matrizen S Und R kann explizit definiert werden:

S 2 = AA t oder S = (AA t) ½ und R = S −1 A = (AA t) −½ A.

Zum Beispiel,

Reis. 20 Polarzerlegung

Wenn die Matrix A entartet ist, dann ist die Zerlegung nicht eindeutig - nämlich: S immer noch allein, aber R es können viele sein. Die polare Zerlegung repräsentiert eine Matrix A als Kompressions/Stretch-Kombination S und drehen R.

2.6. Eigenvektoren und Eigenwerte

Lassen A ist eine quadratische Matrix. Vektor v genannt eigenen Vektor Matrizen A, Wenn

Ein V = λ v,

wo die Zahl λ aufgerufen wird Eigenwert Matrizen A. Also die Transformation, die die Matrix durchführt Aüber Vektor v, wird mit einem Faktor λ auf eine einfache Streckung oder Stauchung reduziert. Der Eigenvektor ist bis auf die Multiplikation mit der Konstanten α ≠ 0 bestimmt, d.h. Wenn v ein Eigenvektor ist, dann α v ist auch ein Eigenvektor.

2.7. Eigenwerte

An der Matrix A, Abmessungen ( N× N) kann nicht größer sein als N Eigenwerte. Sie befriedigen charakteristische Gleichung

det( A − λ ICH) = 0,

Sein algebraische Gleichung N-te Ordnung. Insbesondere hat die charakteristische Gleichung für eine 2×2-Matrix die Form

Zum Beispiel,

Reis. 21 Eigenwerte

Satz von Eigenwerten λ 1 ,..., λ N Matrizen A genannt Spektrum A.

Das Spektrum hat verschiedene Eigenschaften. Insbesondere

det( A) = λ 1×...×λ N, Sp( A) = λ 1 + ... + λ N.

Die Eigenwerte einer beliebigen Matrix können komplexe Zahlen sein, aber wenn die Matrix symmetrisch ist ( A t = A), dann sind seine Eigenwerte reell.

2.8. Eigenvektoren

An der Matrix A, Abmessungen ( N× N) kann nicht größer sein als N Eigenvektoren, von denen jeder seinem eigenen Wert entspricht. Um den Eigenvektor zu bestimmen v N Sie müssen ein System homogener Gleichungen lösen

(A − λ N ICH)v N = 0 .

Es hat eine nicht-triviale Lösung, weil det( A-λ N ICH) = 0.

Zum Beispiel,

Reis. 22 Eigenvektoren

Die Eigenvektoren einer symmetrischen Matrix sind orthogonal.

Ein Eigenvektor einer quadratischen Matrix ist einer, der, wenn er mit einer gegebenen Matrix multipliziert wird, einen kollinearen Vektor ergibt. In einfachen Worten, wenn eine Matrix mit einem Eigenvektor multipliziert wird, bleibt letzterer gleich, wird aber mit einer Zahl multipliziert.

Definition

Ein Eigenvektor ist ein Nicht-Null-Vektor V, der, wenn er mit einer quadratischen Matrix M multipliziert wird, er selbst wird, erhöht um eine Zahl λ. In algebraischer Notation sieht das so aus:

M × V = λ × V,

wobei λ ein Eigenwert der Matrix M ist.

Betrachten wir ein Zahlenbeispiel. Zur Vereinfachung des Schreibens werden die Zahlen in der Matrix durch ein Semikolon getrennt. Nehmen wir an, wir haben eine Matrix:

• M = 0; 4;
• 6; 10.

Lassen Sie uns es mit einem Spaltenvektor multiplizieren:

• V = -2;

Wenn wir eine Matrix mit einem Spaltenvektor multiplizieren, erhalten wir auch einen Spaltenvektor. In streng mathematischer Sprache würde die Formel zum Multiplizieren einer 2 × 2-Matrix mit einem Spaltenvektor wie folgt aussehen:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

M11 bedeutet das Element der Matrix M, das in der ersten Reihe und ersten Spalte steht, und M22 ist das Element, das sich in der zweiten Reihe und zweiten Spalte befindet. Für unsere Matrix sind diese Elemente M11 = 0, M12 = 4, M21 = 6, M22 10. Für einen Spaltenvektor sind diese Werte V11 = –2, V21 = 1. Gemäß dieser Formel erhalten wir Folgendes Ergebnis des Produkts einer quadratischen Matrix mit einem Vektor:

• M × V = 0 × (–2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

Der Einfachheit halber schreiben wir den Spaltenvektor in eine Zeile. Wir haben also die quadratische Matrix mit dem Vektor (-2; 1) multipliziert, was den Vektor (4; -2) ergibt. Offensichtlich ist dies derselbe Vektor multipliziert mit λ = -2. Lambda bezeichnet dabei einen Eigenwert der Matrix.

Der Eigenvektor einer Matrix ist ein kollinearer Vektor, dh ein Objekt, das seine Position im Raum nicht ändert, wenn es mit einer Matrix multipliziert wird. Das Konzept der Kollinearität in der Vektoralgebra ähnelt dem Begriff der Parallelität in der Geometrie. In der geometrischen Interpretation sind kollineare Vektoren parallel gerichtete Segmente unterschiedlicher Länge. Seit der Zeit von Euklid wissen wir, dass eine einzelne Linie unendlich viele parallele Linien hat, daher ist es logisch anzunehmen, dass jede Matrix eine unendliche Anzahl von Eigenvektoren hat.

Aus dem vorherigen Beispiel ist ersichtlich, dass sowohl (-8; 4) als auch (16; -8) und (32, -16) Eigenvektoren sein können. All dies sind kollineare Vektoren, die dem Eigenwert λ = -2 entsprechen. Wenn wir die ursprüngliche Matrix mit diesen Vektoren multiplizieren, erhalten wir als Ergebnis immer noch einen Vektor, der sich um das 2-fache vom Original unterscheidet. Deshalb ist es beim Lösen von Problemen zum Auffinden eines Eigenvektors erforderlich, nur linear unabhängige Vektorobjekte zu finden. Meistens gibt es für eine n × n-Matrix eine n-te Anzahl von Eigenvektoren. Unser Rechner ist für die Analyse von quadratischen Matrizen zweiter Ordnung ausgelegt, daher werden als Ergebnis fast immer zwei Eigenvektoren gefunden, außer wenn sie zusammenfallen.

Im obigen Beispiel kannten wir den Eigenvektor der ursprünglichen Matrix im Voraus und bestimmten visuell die Lambda-Zahl. In der Praxis läuft aber alles andersherum ab: Am Anfang stehen Eigenwerte und erst dann Eigenvektoren.

Lösungsalgorithmus

Schauen wir uns noch einmal die ursprüngliche Matrix M an und versuchen, ihre beiden Eigenvektoren zu finden. Die Matrix sieht also so aus:

• M = 0; 4;
• 6; 10.

Zunächst müssen wir den Eigenwert λ bestimmen, für den wir die Determinante der folgenden Matrix berechnen müssen:

• (0 − λ); 4;
• 6; (10 − λ).

Diese Matrix erhalten durch Subtrahieren des unbekannten λ von den Elementen auf der Hauptdiagonalen. Die Determinante wird durch die Standardformel bestimmt:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Da unser Vektor nicht Null sein darf, nehmen wir die resultierende Gleichung als linear abhängig und setzen unsere Determinante detA gleich Null.

(0 − λ) × (10 − λ) − 24 = 0

Lassen Sie uns die Klammern öffnen und die charakteristische Gleichung der Matrix erhalten:

λ 2 − 10λ − 24 = 0

Dies ist Standard quadratische Gleichung, die nach der Diskriminante zu lösen ist.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 \u003d 100 + 96 \u003d 196

Die Wurzel der Diskriminante ist sqrt(D) = 14, also λ1 = -2, λ2 = 12. Nun müssen wir für jeden Lambda-Wert einen Eigenvektor finden. Drücken wir die Koeffizienten des Systems für λ = -2 aus.

• M − λ × E = 2; 4;
• 6; 12.

In dieser Formel ist E die Identitätsmatrix. Basierend auf der erhaltenen Matrix erstellen wir ein System linearer Gleichungen:

2x + 4y = 6x + 12y

wobei x und y Elemente des Eigenvektors sind.

Lassen Sie uns alle X's auf der linken Seite und alle Y's auf der rechten Seite sammeln. Offensichtlich - 4x = 8y. Teilen Sie den Ausdruck durch - 4 und erhalten Sie x = -2y. Jetzt können wir den ersten Eigenvektor der Matrix bestimmen, indem wir beliebige Werte der Unbekannten nehmen (denken Sie an die Unendlichkeit linear abhängiger Eigenvektoren). Nehmen wir y = 1, dann x = -2. Daher sieht der erste Eigenvektor wie folgt aus: V1 = (–2; 1). Zurück zum Anfang des Artikels. Mit diesem Vektorobjekt haben wir die Matrix multipliziert, um das Konzept eines Eigenvektors zu demonstrieren.

Lassen Sie uns nun den Eigenvektor für λ = 12 finden.

• M – λ × E = –12; 4
• 6; -2.

Lassen Sie uns dasselbe System linearer Gleichungen aufstellen;

• -12x + 4y = 6x − 2y
• -18x = -6y
• 3x=y.

Nehmen wir nun x = 1, also y = 3. Somit sieht der zweite Eigenvektor wie folgt aus: V2 = (1; 3). Beim Multiplizieren der ursprünglichen Matrix mit diesem Vektor ist das Ergebnis immer derselbe Vektor multipliziert mit 12. Damit ist der Lösungsalgorithmus abgeschlossen. Jetzt wissen Sie, wie Sie einen Eigenvektor einer Matrix manuell definieren.

• bestimmend;
• verfolgen, dh die Summe der Elemente auf der Hauptdiagonalen;
• Rang, d. h. die maximale Anzahl linear unabhängiger Zeilen/Spalten.

Das Programm arbeitet nach dem obigen Algorithmus, wodurch der Lösungsprozess minimiert wird. Es ist wichtig darauf hinzuweisen, dass das Lambda im Programm mit dem Buchstaben "c" bezeichnet wird. Schauen wir uns ein Zahlenbeispiel an.

Programmbeispiel

Versuchen wir, Eigenvektoren für die folgende Matrix zu definieren:

• M=5; 13;
• 4; 14.

Lassen Sie uns diese Werte in die Zellen des Taschenrechners eingeben und die Antwort in der folgenden Form erhalten:

• Matrixrang: 2;
• Matrixdeterminante: 18;
• Matrixspur: 19;
• Eigenvektorberechnung: c 2 − 19,00 c + 18,00 (charakteristische Gleichung);
• Eigenvektorberechnung: 18 (erster Lambdawert);
• Eigenvektorberechnung: 1 (zweiter Lambdawert);
• Gleichungssystem von Vektor 1: -13x1 + 13y1 = 4x1 − 4y1;
• Vektor-2-Gleichungssystem: 4x1 + 13y1 = 4x1 + 13y1;
• Eigenvektor 1: (1; 1);
• Eigenvektor 2: (-3,25; 1).

Somit haben wir zwei linear unabhängige Eigenvektoren erhalten.

Abschluss

Lineare Algebra u analytische Geometrie- Standardfächer für jeden Studienanfänger einer technischen Fachrichtung. Große Menge Vektoren und Matrizen ist erschreckend, und es ist leicht, bei solch umständlichen Berechnungen einen Fehler zu machen. Unser Programm ermöglicht es den Schülern, ihre Berechnungen zu überprüfen oder automatisch das Problem zu lösen, einen Eigenvektor zu finden. Es gibt andere lineare Algebra-Rechner in unserem Katalog, verwenden Sie sie in Ihrem Studium oder Ihrer Arbeit.

Definition 9.3. Vektor X genannt eigenen Vektor Matrizen A wenn es eine solche Nummer gibt λ, dass die Gleichheit gilt: A X= λ X, das heißt, das Ergebnis der Anwendung auf X lineare Transformation durch die Matrix gegeben A, ist die Multiplikation dieses Vektors mit der Zahl λ . Die Nummer selbst λ genannt eigene Nummer Matrizen A.

Einsetzen in Formeln (9.3) x` j = λx j , wir erhalten ein Gleichungssystem zur Bestimmung der Koordinaten des Eigenvektors:

. (9.5)

Dieses lineare homogene System hat nur dann eine nichttriviale Lösung, wenn seine Hauptdeterminante 0 ist (Cramer-Regel). Indem Sie diese Bedingung in der Form schreiben:

wir erhalten eine Gleichung zur Bestimmung der Eigenwerte λ genannt charakteristische Gleichung. Kurz zusammengefasst lässt es sich wie folgt darstellen:

| A-λE | = 0, (9.6)

da seine linke Seite die Determinante der Matrix ist A-λE. Polynom bzgl λ | A-λE| genannt charakteristisches Polynom Matrizen a.

Eigenschaften des charakteristischen Polynoms:

1) Das charakteristische Polynom einer linearen Transformation hängt nicht von der Wahl der Basis ab. Nachweisen. (siehe (9.4)), aber somit, . Es kommt also nicht auf die Wahl der Basis an. Daher und | A-λE| ändert sich beim Übergang auf eine neue Basis nicht.

2) Wenn die Matrix A lineare Transformation ist symmetrisch(diese. ein ij = ein ji), dann alle Wurzeln charakteristische Gleichung(9.6) sind reelle Zahlen.

Eigenschaften von Eigenwerten und Eigenvektoren:

1) Wenn wir eine Basis aus Eigenvektoren wählen x 1, x 2, x 3 entsprechend den Eigenwerten λ 1 , λ 2 , λ 3 Matrizen A, dann hat in dieser Basis die lineare Transformation A eine Diagonalmatrix:

(9.7) Der Beweis dieser Eigenschaft folgt aus der Definition von Eigenvektoren.

2) Wenn die Transformationseigenwerte A unterschiedlich sind, dann sind die ihnen entsprechenden Eigenvektoren linear unabhängig.

3) Wenn das charakteristische Polynom der Matrix A hat drei verschiedene Wurzeln, dann in gewisser Weise die Matrix A hat eine diagonale Form.

Finden wir die Eigenwerte und Eigenvektoren der Matrix. Machen wir die charakteristische Gleichung: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Finden Sie die Koordinaten der Eigenvektoren, die jedem gefundenen Wert entsprechen λ. Aus (9.5) folgt, wenn X (1) ={x1, x2, x3) ist der zugehörige Eigenvektor λ 1 = -2, dann

ist ein kooperatives, aber unbestimmtes System. Seine Lösung kann geschrieben werden als X (1) ={A,0,-A), wobei a eine beliebige Zahl ist. Insbesondere, wenn Sie das verlangen | X (1) |=1, X (1) =

Einsetzen in das System (9.5) λ 2 = 3 erhalten wir ein System zur Bestimmung der Koordinaten des zweiten Eigenvektors - X (2) ={y1,y2,y3}:

, Wo X (2) ={b,-b,b) oder, sofern | X (2) |=1, X (2) =

Für λ 3 = 6 Finden Sie den Eigenvektor X (3) ={z1, z2, z3}:

, X (3) ={C,2c,c) oder in der normalisierten Version

x (3) = Man kann sehen, dass X (1) X (2) = ab-ab= 0, X (1) X (3) = ac-ac= 0, X (2) X (3) = v. Chr- 2bc + bc= 0. Somit sind die Eigenvektoren dieser Matrix paarweise orthogonal.

Vortrag 10

Quadratische Formen und ihr Zusammenhang mit symmetrischen Matrizen. Eigenschaften von Eigenvektoren und Eigenwerten einer symmetrischen Matrix. Reduktion einer quadratischen Form auf eine kanonische Form.

Definition 10.1.quadratische Form echte Variablen x 1, x 2, …, x n ein Polynom zweiten Grades bezüglich dieser Variablen heißt, das keinen freien Term und Terme ersten Grades enthält.

Beispiele für quadratische Formen:

(N = 2),

(N = 3). (10.1)

Erinnern Sie sich an die Definition einer symmetrischen Matrix aus der letzten Vorlesung:

Definition 10.2. Die quadratische Matrix heißt symmetrisch, wenn , also wenn die zur Hauptdiagonale symmetrischen Matrixelemente gleich sind.

Eigenschaften von Eigenwerten und Eigenvektoren einer symmetrischen Matrix:

1) Alle Eigenwerte einer symmetrischen Matrix sind reell.

Beweis (z N = 2).

Lassen Sie die Matrix A sieht aus wie: . Stellen wir die charakteristische Gleichung auf:

(10.2) Finde die Diskriminante:

Daher hat die Gleichung nur reelle Wurzeln.

2) Die Eigenvektoren einer symmetrischen Matrix sind orthogonal.

Beweis (z N= 2).

Die Koordinaten der Eigenvektoren und müssen die Gleichungen erfüllen.

Matrizen vom Diagonaltyp sind am einfachsten angeordnet. Es stellt sich die Frage, ob es möglich ist, eine Basis zu finden, in der die Matrix eines linearen Operators eine Diagonalform hätte. Eine solche Grundlage ist vorhanden.
Gegeben sei ein linearer Raum R n und ein darin wirkender linearer Operator A; in diesem Fall nimmt der Operator A R n in sich auf, also A:R n → R n .

Definition. Ein Nicht-Null-Vektor heißt Eigenvektor des Operators A, wenn der Operator A in einen zu ihm kollinearen Vektor übersetzt wird, d. h. Die Zahl λ heißt Eigenwert oder Eigenwert des Operators A, der dem Eigenvektor entspricht.
Wir bemerken einige Eigenschaften von Eigenwerten und Eigenvektoren.
1. Beliebige Linearkombination von Eigenvektoren des Operators A, der demselben Eigenwert λ entspricht, ist ein Eigenvektor mit demselben Eigenwert.
2. Eigenvektoren Operator A mit paarweise verschiedenen Eigenwerten λ 1 , λ 2 , …, λ m sind linear unabhängig.
3. Sind die Eigenwerte λ 1 = λ 2 = λ m = λ, dann entspricht der Eigenwert λ höchstens m linear unabhängigen Eigenvektoren.

Also, wenn es n linear unabhängige Eigenvektoren gibt entsprechend unterschiedlichen Eigenwerten λ 1 , λ 2 , …, λ n , dann sind sie linear unabhängig, daher können sie dem Raum R n zugrunde gelegt werden. Finden wir die Form der Matrix des linearen Operators A in der Basis seiner Eigenvektoren, für die wir mit dem Operator A auf den Basisvektoren operieren: Dann .
Somit hat die Matrix des linearen Operators A auf der Basis ihrer Eigenvektoren eine diagonale Form und die Eigenwerte des Operators A liegen auf der Diagonale.
Gibt es eine andere Basis, in der die Matrix eine Diagonalform hat? Die Antwort auf diese Frage liefert der folgende Satz.

Satz. Die Matrix eines linearen Operators A in der Basis (i = 1..n) hat genau dann Diagonalform, wenn alle Vektoren der Basis Eigenvektoren des Operators A sind.

Regel zum Finden von Eigenwerten und Eigenvektoren

Lassen Sie den Vektor , wobei x 1 , x 2 , …, x n - Koordinaten des Vektors relativ zur Basis und ist der Eigenvektor des linearen Operators A entsprechend dem Eigenwert λ , d.h. Diese Beziehung kann in Matrixform geschrieben werden

. (*)

Gleichung (*) kann als Gleichung zum Auffinden von , und betrachtet werden, das heißt, wir interessieren uns für nicht triviale Lösungen, da der Eigenvektor nicht null sein kann. Es ist bekannt, dass nicht-triviale Lösungen homogenes System lineare Gleichungen existieren genau dann, wenn det(A - λE) = 0. Damit λ ein Eigenwert des Operators A ist, ist es also notwendig und ausreichend, dass det(A - λE) = 0 ist.
Wenn die Gleichung (*) im Detail in Koordinatenform geschrieben wird, erhalten wir ein System linearer homogener Gleichungen:

(1)
Wo ist die Matrix des linearen Operators.

System (1) hat eine von Null verschiedene Lösung, wenn seine Determinante D gleich Null ist

Wir haben eine Gleichung zum Finden von Eigenwerten.
Diese Gleichung heißt charakteristische Gleichung und ihre linke Seite heißt charakteristisches Polynom der Matrix (Operator) A. Wenn das charakteristische Polynom keine reellen Wurzeln hat, dann hat die Matrix A keine Eigenvektoren und kann nicht auf eine Diagonalform reduziert werden.
Seien λ 1 , λ 2 , …, λ n die reellen Wurzeln der charakteristischen Gleichung, und es können Vielfache davon vorkommen. Setzen wir diese Werte wiederum in System (1) ein, finden wir die Eigenvektoren.

Beispiel 12. Der lineare Operator A wirkt im R 3 nach dem Gesetz , wobei x 1 , x 2 , ..., x n die Koordinaten des Vektors in der Basis sind , , . Finden Sie die Eigenwerte und Eigenvektoren dieses Operators.
Lösung. Wir bauen die Matrix dieses Operators:
.
Wir stellen ein System zur Bestimmung der Koordinaten von Eigenvektoren zusammen:

Wir stellen die charakteristische Gleichung auf und lösen sie:

.
λ 1,2 = -1, λ 3 = 3.
Setzen wir λ = -1 in das System ein, haben wir:
oder
Als , dann gibt es zwei abhängige Variablen und eine freie Variable.
Sei also x 1 eine freie Unbekannte Wir lösen dieses System auf beliebige Weise und finden die allgemeine Lösung dieses Systems: Das fundamentale Lösungssystem besteht aus einer Lösung, da n - r = 3 - 2 = 1.
Der dem Eigenwert λ = -1 entsprechende Satz von Eigenvektoren hat die Form: , wobei x 1 eine beliebige Zahl ungleich Null ist. Wählen wir einen Vektor aus dieser Menge, indem wir beispielsweise x 1 = 1 setzen: .
Ähnlich argumentierend finden wir den Eigenvektor, der dem Eigenwert λ = 3 entspricht: .
Im Raum R 3 besteht die Basis aus drei linear unabhängigen Vektoren, aber wir haben nur zwei linear unabhängige Eigenvektoren erhalten, aus denen die Basis im R 3 nicht gebildet werden kann. Folglich kann die Matrix A eines linearen Operators nicht auf eine diagonale Form reduziert werden.

Beispiel 13 Gegeben eine Matrix .
1. Beweisen Sie, dass der Vektor ein Eigenvektor der Matrix A ist. Finden Sie den Eigenwert, der diesem Eigenvektor entspricht.
2. Finden Sie eine Basis, in der die Matrix A eine Diagonalform hat.
Lösung.
1. Wenn , dann ist ein Eigenvektor

.
Vektor (1, 8, -1) ist ein Eigenvektor. Eigenwert λ = -1.
Die Matrix hat eine diagonale Form in der Basis, die aus Eigenvektoren besteht. Einer von ihnen ist berühmt. Finden wir den Rest.
Wir suchen nach Eigenvektoren aus dem System:

Charakteristische Gleichung: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ2 - 1) = 0
λ 1 = –3, λ 2 = 1, λ 3 = –1.
Finden Sie den Eigenvektor, der dem Eigenwert λ = -3 entspricht:

Der Rang der Matrix dieses Systems ist gleich zwei und ist gleich der Anzahl der Unbekannten, daher hat dieses System nur eine Nulllösung x 1 = x 3 = 0. x 2 kann hier beispielsweise alles andere als Null sein, x 2 = 1. Somit ist der Vektor (0 ,1,0) ein Eigenvektor entsprechend λ = –3. Lass uns das Prüfen:
.
Wenn λ = 1, dann erhalten wir das System
Der Rang der Matrix ist zwei. Streiche die letzte Gleichung durch.
Sei x 3 die freie Unbekannte. Dann x 1 \u003d -3x 3, 4x 2 \u003d 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
Unter der Annahme x 3 = 1 haben wir (-3,-9,1) - einen Eigenvektor, der dem Eigenwert λ = 1 entspricht. Prüfen Sie:

.
Da die Eigenwerte reell und unterschiedlich sind, sind die ihnen entsprechenden Vektoren linear unabhängig, sodass sie in R 3 zugrunde gelegt werden können. Also in der Basis , , Matrix A hat die Form:
.
Nicht jede Matrix eines linearen Operators A:R n → R n kann auf eine Diagonalform reduziert werden, da es für einige lineare Operatoren weniger als n linear unabhängige Eigenvektoren geben kann. Ist die Matrix jedoch symmetrisch, so entsprechen genau m linear unabhängige Vektoren der Wurzel der charakteristischen Gleichung der Multiplizität m.

Definition. Eine symmetrische Matrix ist eine quadratische Matrix, in der die Elemente, die in Bezug auf die Hauptdiagonale symmetrisch sind, gleich sind, dh in der .
Bemerkungen. 1. Alle Eigenwerte einer symmetrischen Matrix sind reell.
2. Eigenvektoren einer symmetrischen Matrix, die paarweise unterschiedlichen Eigenwerten entsprechen, sind orthogonal.
Als eine der zahlreichen Anwendungen des untersuchten Apparats betrachten wir das Problem der Bestimmung der Form einer Kurve zweiter Ordnung.

www.site ermöglicht es Ihnen, zu finden. Die Website führt die Berechnung durch. In wenigen Sekunden gibt der Server die richtige Lösung. Die charakteristische Gleichung für die Matrix wird ein algebraischer Ausdruck sein, der von der Regel zur Berechnung der Determinante gefunden wird Matrizen Matrizen, während es auf der Hauptdiagonale Unterschiede in den Werten der Diagonalelemente und der Variablen gibt. Beim Rechnen charakteristische gleichung für matrix online, jedes Element Matrizen wird mit den entsprechenden anderen Elementen multipliziert Matrizen. Finden Sie im Modus online nur für Quadrat möglich Matrizen. Betrieb finden charakteristische gleichung für matrix online reduziert sich auf die Berechnung der algebraischen Summe des Produkts der Elemente Matrizen als Ergebnis der Ermittlung der Determinante Matrizen, nur zum Zwecke der Feststellung charakteristische gleichung für matrix online. Diese Operation nimmt in der Theorie einen besonderen Platz ein Matrizen, ermöglicht es Ihnen, Eigenwerte und Vektoren mithilfe von Wurzeln zu finden. Aufgabe finden charakteristische gleichung für matrix online ist, Elemente zu multiplizieren Matrizen mit der anschließenden Summierung dieser Produkte nach einer bestimmten Regel. www.site findet charakteristische Gleichung für Matrix gegebene Dimension im Modus online. Berechnung charakteristische gleichung für matrix online für eine gegebene Dimension ist dies das Finden eines Polynoms mit numerischen oder symbolischen Koeffizienten, die durch die Regel zur Berechnung der Determinante gefunden werden Matrizen- als Summe der Produkte der entsprechenden Elemente Matrizen, nur zum Zwecke der Feststellung charakteristische gleichung für matrix online. Finden eines Polynoms bezüglich einer Variablen für ein Quadrat Matrizen, als Definition charakteristische Gleichung für die Matrix, theoretisch üblich Matrizen. Der Wert der Wurzeln des Polynoms charakteristische gleichung für matrix online verwendet, um Eigenvektoren und Eigenwerte für zu definieren Matrizen. Wenn jedoch die Determinante Matrizen wird dann null sein Matrix charakteristische Gleichung wird immer noch bestehen, im Gegensatz zum Gegenteil Matrizen. Um zu rechnen charakteristische Gleichung für Matrix oder mehrere auf einmal suchen Matrizen charakteristische Gleichungen, müssen Sie viel Zeit und Mühe aufwenden, während unser Server findet charakteristische Gleichung für Online-Matrix. In diesem Fall die Antwort durch Finden charakteristische gleichung für matrix online wird korrekt und mit ausreichender Genauigkeit sein, auch wenn die Zahlen beim Auffinden charakteristische gleichung für matrix online wird irrational sein. Auf der Seite www.site Zeicheneingaben sind in Elementen erlaubt Matrizen, also charakteristische Gleichung für Online-Matrix kann beim Rechnen in allgemeiner symbolischer Form dargestellt werden Kennliniengleichungsmatrix online. Es ist nützlich, die erhaltene Antwort zu überprüfen, wenn das Problem des Findens gelöst wird charakteristische gleichung für matrix online Nutzung der Website www.site. Bei der Berechnung eines Polynoms - charakteristische Gleichung der Matrix, ist es notwendig, bei der Lösung dieses Problems aufmerksam und äußerst konzentriert zu sein. Im Gegenzug hilft Ihnen unsere Website, Ihre Entscheidung zu diesem Thema zu überprüfen Kennliniengleichungsmatrix online. Wenn Sie keine Zeit für lange Überprüfungen gelöster Probleme haben, dann www.site sicher ein praktisches Hilfsmittel zur Kontrolle beim Finden und Rechnen charakteristische gleichung für matrix online.