Let CB X form a general population and let β be the unknown parameter CB X. If the statistical estimate in * is consistent, then the larger the sample size, the more accurately we obtain the value of β. However, in practice, we do not have very large samples, so we cannot guarantee greater accuracy.

Let b* be a statistical estimate for c. Value |in* - in| is called estimation accuracy. It is clear that the accuracy is CB, since β* is a random variable. Let us specify a small positive number 8 and require that the accuracy of the estimate |в* - в| was less than 8, i.e. | in* - in |< 8.

Reliability g or confidence probability of an estimate in in * is the probability g with which the inequality |in * - in|< 8, т. е.

Typically, reliability g is specified in advance, and g is taken to be a number close to 1 (0.9; 0.95; 0.99; ...).

Since the inequality |in * - in|< S равносильно двойному неравенству в* - S < в < в* + 8, то получаем:

The interval (in * - 8, in * + 5) is called a confidence interval, i.e. confidence interval covers the unknown parameter in with probability y. Note that the ends of the confidence interval are random and vary from sample to sample, so it is more accurate to say that the interval (in * - 8, in * + 8) covers the unknown parameter in, rather than in belongs to this interval.

Let population is given by a random variable X, distributed according to a normal law, and the standard deviation a is known. Unknown is expected value a = M(X). It is required to find the confidence interval for a for a given reliability y.

Sample mean

is statistical assessment for xg = a.

Theorem. Random value xB has normal distribution, if X has a normal distribution, and M (XB) = a,

A (XB) = a, where a = y/B (X), a = M (X). l/i

The confidence interval for a has the form:

We find 8.

Using the ratio

where Ф(r) is the Laplace function, we have:

P ( | XB - a |<8} = 2Ф

table of values ​​of the Laplace function we find the value of t.

Having designated

T, we get F(t) = g Since g is given, then by

From the equality we find that the estimate is accurate.

This means that the confidence interval for a has the form:

Given a sample from the population X

ng	To"	X2	Xm
n.	n1	n2	nm

n = U1 + ... + nm, then the confidence interval will be:

Example 6.35. Find the confidence interval for estimating the mathematical expectation a of the normal distribution with a reliability of 0.95, knowing the sample mean Xb = 10.43, sample size n = 100 and standard deviation s = 5.

Let's use the formula

And others. All of them are estimates of their theoretical analogues, which could be obtained if not a sample, but a general population were available. But alas, the general population is very expensive and often inaccessible.

The concept of interval estimation

Any sample estimate has some spread, because is a random variable depending on the values ​​in a particular sample. Therefore, for more reliable statistical conclusions, one should know not only the point estimate, but also the interval, which with a high probability γ (gamma) covers the evaluated indicator θ (theta).

Formally, these are two such values ​​(statistics) T 1 (X) And T 2 (X), What T 1< T 2 , for which at a given probability level γ the condition is met:

In short, it is likely γ or more the true indicator is between the points T 1 (X) And T 2 (X), which are called the lower and upper bounds confidence interval.

One of the conditions for constructing confidence intervals is its maximum narrowness, i.e. it should be as short as possible. The desire is quite natural, because... the researcher tries to more accurately localize the location of the desired parameter.

It follows that the confidence interval must cover the maximum probabilities of the distribution. and the assessment itself should be in the center.

That is, the probability of deviation (of the true indicator from the estimate) upward is equal to the probability of deviation downward. It should also be noted that for asymmetric distributions, the interval on the right is not equal to the interval on the left.

The figure above clearly shows that the greater the confidence probability, the wider the interval - a direct relationship.

This was a short introduction to the theory of interval estimation of unknown parameters. Let's move on to finding confidence limits for the mathematical expectation.

Confidence interval for mathematical expectation

If the original data are distributed over , then the average will be a normal value. This follows from the rule that a linear combination of normal values ​​also has a normal distribution. Therefore, to calculate probabilities we could use the mathematical apparatus of the normal distribution law.

However, this will require knowing two parameters - expectation and variance, which are usually unknown. You can, of course, use estimates instead of parameters (arithmetic mean and ), but then the distribution of the average will not be entirely normal, it will be slightly flattened downward. This fact was cleverly noted by citizen William Gosset from Ireland, publishing his discovery in the March 1908 issue of the journal Biometrica. For purposes of secrecy, Gosset signed himself Student. This is how the Student t-distribution appeared.

However, the normal distribution of data, used by K. Gauss in analyzing errors in astronomical observations, is extremely rare in earthly life and is quite difficult to establish (about 2 thousand observations are needed for high accuracy). Therefore, it is best to discard the assumption of normality and use methods that do not depend on the distribution of the original data.

The question arises: what is the distribution of the arithmetic mean if it is calculated from the data of an unknown distribution? The answer is given by the well-known in probability theory Central limit theorem(CPT). In mathematics, there are several variants of it (the formulations have been refined over the years), but all of them, roughly speaking, boil down to the statement that the sum of a large number of independent random variables obeys the normal distribution law.

When calculating the arithmetic mean, the sum of random variables is used. From here it turns out that the arithmetic mean has a normal distribution, in which the expectation is the expectation of the original data, and the variance is .

Smart people know how to prove CLT, but we will verify this with the help of an experiment conducted in Excel. Let's simulate a sample of 50 uniformly distributed random variables (using the Excel function RANDBETWEEN). Then we will make 1000 such samples and calculate the arithmetic mean for each. Let's look at their distribution.

It can be seen that the distribution of the average is close to the normal law. If the sample size and number are made even larger, the similarity will be even better.

Now that we have seen with our own eyes the validity of the CLT, we can, using , calculate confidence intervals for the arithmetic mean, which cover the true mean or mathematical expectation with a given probability.

To establish the upper and lower limits, you need to know the parameters of the normal distribution. As a rule, there are none, so estimates are used: arithmetic mean And sample variance. I repeat, this method gives a good approximation only with large samples. When samples are small, it is often recommended to use the Student distribution. Don't believe it! The Student distribution for the mean occurs only when the original data is normally distributed, that is, almost never. Therefore, it is better to immediately set a minimum bar for the amount of required data and use asymptotically correct methods. They say 30 observations are enough. Take 50 - you won't go wrong.

T 1.2– lower and upper limits of the confidence interval

– sample arithmetic mean

s 0– standard deviation of the sample (unbiased)

n – sample size

γ – confidence probability (usually equal to 0.9, 0.95 or 0.99)

c γ =Φ -1 ((1+γ)/2)– the inverse value of the standard normal distribution function. Simply put, this is the number of standard errors from the arithmetic mean to the lower or upper bound (these three probabilities correspond to values ​​of 1.64, 1.96 and 2.58).

The essence of the formula is that the arithmetic mean is taken and then a certain amount is set aside from it ( with γ) standard errors ( s 0 /√n). Everything is known, take it and consider it.

Before the widespread use of personal computers, they used to obtain the values ​​of the normal distribution function and its inverse. They are still used today, but it is more effective to use ready-made Excel formulas. All elements from the formula above ( , and ) can be easily calculated in Excel. But there is a ready-made formula for calculating the confidence interval - TRUST.NORM. Its syntax is as follows.

CONFIDENCE.NORM(alpha;standard_off;size)

alpha– significance level or confidence level, which in the notation adopted above is equal to 1- γ, i.e. the probability that the mathematicalthe expectation will be outside the confidence interval. With a confidence level of 0.95, alpha is 0.05, etc.

standard_off– standard deviation of sample data. There is no need to calculate the standard error; Excel itself will divide by the root of n.

size– sample size (n).

The result of the CONFIDENCE NORM function is the second term from the formula for calculating the confidence interval, i.e. half-interval Accordingly, the lower and upper points are the average ± the obtained value.

Thus, it is possible to construct a universal algorithm for calculating confidence intervals for the arithmetic mean, which does not depend on the distribution of the original data. The price for universality is its asymptotic nature, i.e. the need to use relatively large samples. However, in the age of modern technology, collecting the required amount of data is usually not difficult.

Testing statistical hypotheses using confidence intervals

(module 111)

One of the main problems solved in statistics is. Its essence is briefly as follows. An assumption is made, for example, that the expectation of the general population is equal to some value. Then the distribution of sample means that can be observed for a given expectation is constructed. Next, they look at where in this conditional distribution the real average is located. If it goes beyond acceptable limits, then the appearance of such an average is very unlikely, and if the experiment is repeated once, it is almost impossible, which contradicts the hypothesis put forward, which is successfully rejected. If the average does not go beyond the critical level, then the hypothesis is not rejected (but also not proven!).

So, with the help of confidence intervals, in our case for expectation, you can also test some hypotheses. It's very easy to do. Let's say the arithmetic mean for a certain sample is equal to 100. The hypothesis is tested that the expected value is, say, 90. That is, if we pose the question primitively, it sounds like this: can it be that with the true value of the mean equal to 90, the observed the average turned out to be 100?

To answer this question, you will additionally need information about standard deviation and sample size. Let's assume the standard deviation is 30 and the number of observations is 64 (to easily extract the root). Then the standard error of the mean is 30/8 or 3.75. To calculate a 95% confidence interval, you will need to add two standard errors to each side of the mean (more precisely, 1.96). The confidence interval will be approximately 100±7.5 or from 92.5 to 107.5.

Further reasoning is as follows. If the value being tested falls within the confidence interval, then it does not contradict the hypothesis, because falls within the limits of random fluctuations (with a probability of 95%). If the point being checked falls outside the confidence interval, then the probability of such an event is very small, in any case below the acceptable level. This means that the hypothesis is rejected as contradicting the observed data. In our case, the hypothesis about the expected value is outside the confidence interval (the tested value of 90 is not included in the interval 100±7.5), so it should be rejected. Answering the primitive question above, it should be said: no, it cannot, in any case, this happens extremely rarely. Often, they indicate the specific probability of erroneously rejecting the hypothesis (p-level), and not the specified level on which the confidence interval was constructed, but more on that another time.

As you can see, constructing a confidence interval for the average (or mathematical expectation) is not difficult. The main thing is to grasp the essence, and then things will move on. In practice, most cases use a 95% confidence interval, which is approximately two standard errors wide on either side of the mean.

That's all for now. All the best!

CONFIDENCE INTERVAL FOR MATHEMATICAL EXPECTATION

1. Let it be known that sl. the quantity x obeys the normal law with unknown mean μ and known σ 2: X~N(μ,σ 2), σ 2 is given, μ is unknown. β is given. Based on the sample x 1, x 2, … , x n, it is necessary to construct I β (θ) (now θ=μ), satisfying (13)

The sample mean (also called sample mean) obeys the normal law with the same center μ, but smaller variance X~N (μ, D), where variance D =σ 2 =σ 2 /n.

We will need the number K β, defined for ξ~N(0,1) by the condition

In words: between the points -K β and K β of the abscissa axis lies the area under the density curve of the standard normal law, equal to β

For example, K 0.90 = 1.645 quantile of the 0.95 level of value ξ

K 0.95 = 1.96. ; K 0.997 =3.

In particular, setting aside 1.96 standard deviations to the right and the same to the left from the center of any normal law, we capture the area under the density curve equal to 0.95, due to which K 0 95 is a quantile of the level 0.95 + 1/2 * 0.005 = 0.975 for this law.

The required confidence interval for the general mean μ is I A (μ) = (x-σ, x+σ),

where δ = (15)

Let's give a rationale:

According to what has been said, words. the value falls into the interval J=μ±σ with probability β (Fig. 9). In this case, the quantity deviates from the center μ by less than δ, and the random interval ± δ (with a random center and the same width as J) will cover the point μ. That is Є J<=> μ Є Iβ, and therefore Р(μЄІ β) = Р(Є J)=β.

So, the interval I β, constant over the sample, contains the mean μ with probability β.

Clearly, the larger n, the smaller σ and the interval is narrower, and the larger we take the guarantee β, the wider the confidence interval.

Example 21.

Based on a sample with n=16 for a normal value with a known variance σ 2 =64, x=200 was found. Construct a confidence interval for the general mean (in other words, for the mathematical expectation) μ, taking β=0.95.

Solution. I β (μ)= ± δ, where δ = K β σ/ -> K β σ/ =1.96*8/ = 4

I 0.95 (μ)=200 4=(196;204).

Concluding that with a guarantee of β=0.95 the true average belongs to the interval (196,204), we understand that an error is possible.

Out of 100 confidence intervals I 0.95 (μ), on average 5 do not contain μ.

Example 22.

In the conditions of the previous example 21, what should n be taken to narrow the confidence interval by half? To have 2δ=4, we must take

In practice, one-sided confidence intervals are often used. Thus, if high values ​​of μ are useful or not harmful, but low values ​​are unpleasant, as in the case of strength or reliability, then it is reasonable to construct a one-sided interval. To do this, you should raise its upper limit as much as possible. If we construct, as in Example 21, a two-sided confidence interval for a given β, and then expand it as much as possible at the expense of one of the boundaries, we obtain a one-sided interval with a greater guarantee β" = β + (1-β) / 2 = (1+ β)/2, for example, if β = 0.90, then β = 0.90 + 0.10/2 = 0.95.

For example, we will assume that we are talking about the strength of the product and raise the upper limit of the interval to . Then for μ in example 21 we obtain a one-sided confidence interval (196,°°) with a lower limit of 196 and a confidence probability β"=0.95+0.05/2=0.975.

A practical disadvantage of formula (15) is that it is derived under the assumption that the variance = σ 2 (hence = σ 2 /n) is known; and this rarely happens in life. The exception is the case when the sample size is large, say, n is measured in hundreds or thousands, and then for σ 2 one can practically take its estimate s 2 or .

Example 23.

Let's assume that in a large city, as a result of a sample survey of the living conditions of residents, the following table of data was obtained (example from work).

Table 8

Source data for example

It is natural to assume that the value X is the total (usable) area (in m2) per person and obeys the normal law. The mean μ and variance σ 2 are unknown. For μ, a 95% confidence interval needs to be constructed. In order to find sample means and variance using grouped data, we will compile the following table of calculations (Table 9).

Table 9

Calculating X and 5 from grouped data

N groups 3	Total area per person, m2	Number of residents in group r j	Midpoint of the interval x j	r j x j	rjxj 2
	Up to 5.0		2.5	20.0	50.0
	5.0-10.0		7.5	712.5	5343.75
	10.0-15.0		12.5	2550.0	31875.0
	15.0-20.0		17.5	4725.0	82687.5
	20.0-25.0		22.5	4725.0	106312.5
	25.0-30.0		27.5	3575.0	98312.5
	more than 30.0		32.5 *	2697.5	87668.75
			-	19005.0	412250.0

In this auxiliary table, the first and second initial statistical moments are calculated using formula (2) a 1 And A 2

Although the variance σ 2 is unknown here, due to the large sample size, we can practically apply formula (15), putting σ = = 7.16 in it.

Then δ=k 0.95 σ/ =1.96*7.16/ =0.46.

The confidence interval for the general average at β=0.95 is equal to I 0.95 (μ) = ± δ = 19 ± 0.46 = (18.54; 19.46).

Consequently, the average value of area per person in a given city with a guarantee of 0.95 lies in the interval (18.54; 19.46).

2. Confidence interval for the mathematical expectation μ in the case of an unknown variance σ 2 of the normal value.

(16)

This interval for a given guarantee β is constructed according to the formula, where ν = n-1,

.

The coefficient t β,ν has the same meaning for the t distribution with ν degrees of freedom as β for the distribution N(0,1), namely:

In other words, sl. The value tν falls into the interval (-t β,ν ; +t β,ν) with probability β. The values ​​of t β,ν are given in Table 10 for β=0.95 and β=0.99.

Table 10.

Values ​​t β,ν

Returning to example 23, we see that in it the confidence interval was constructed according to formula (16) with the coefficient t β,υ =k 0..95 =1.96, since n=1000. - this is an interval calculated from data that, with a known probability, contains the mathematical expectation of the general population. A natural estimate for the mathematical expectation is the arithmetic mean of its observed values. Therefore, throughout the lesson we will use the terms “average” and “average value”. In problems of calculating a confidence interval, an answer most often required is something like “The confidence interval of the average number [value in a particular problem] is from [smaller value] to [larger value].” Using a confidence interval, you can evaluate not only average values, but also the proportion of a particular characteristic of the general population. Average values, dispersion, standard deviation and error, through which we will arrive at new definitions and formulas, are discussed in the lesson Characteristics of the sample and population .

Point and interval estimates of the mean

If the average value of the population is estimated by a number (point), then a specific average, which is calculated from a sample of observations, is taken as an estimate of the unknown average value of the population. In this case, the value of the sample mean - a random variable - does not coincide with the mean value of the general population. Therefore, when indicating the sample mean, you must simultaneously indicate the sampling error. The measure of sampling error is the standard error, which is expressed in the same units as the mean. Therefore, the following notation is often used: .

If the estimate of the average needs to be associated with a certain probability, then the parameter of interest in the population must be assessed not by one number, but by an interval. A confidence interval is an interval in which, with a certain probability P the value of the estimated population indicator is found. Confidence interval in which it is probable P = 1 - α the random variable is found, calculated as follows:

,

α = 1 - P, which can be found in the appendix to almost any book on statistics.

In practice, the population mean and variance are not known, so the population variance is replaced by the sample variance, and the population mean by the sample mean. Thus, the confidence interval in most cases is calculated as follows:

.

The confidence interval formula can be used to estimate the population mean if

• the standard deviation of the population is known;
• or the standard deviation of the population is unknown, but the sample size is greater than 30.

The sample mean is an unbiased estimate of the population mean. In turn, the sample variance is not an unbiased estimate of the population variance. To obtain an unbiased estimate of the population variance in the sample variance formula, sample size n should be replaced by n-1.

Example 1. Information was collected from 100 randomly selected cafes in a certain city that the average number of employees in them is 10.5 with a standard deviation of 4.6. Determine the 95% confidence interval for the number of cafe employees.

where is the critical value of the standard normal distribution for the significance level α = 0,05 .

Thus, the 95% confidence interval for the average number of cafe employees ranged from 9.6 to 11.4.

Example 2. For a random sample from the population of 64 observations, the following total values ​​were calculated:

sum of values ​​in observations,

sum of squared deviations of values ​​from the average .

Calculate the 95% confidence interval for the mathematical expectation.

Let's calculate the standard deviation:

,

Let's calculate the average value:

.

We substitute the values ​​into the expression for the confidence interval:

where is the critical value of the standard normal distribution for the significance level α = 0,05 .

We get:

Thus, the 95% confidence interval for the mathematical expectation of this sample ranged from 7.484 to 11.266.

Example 3. For a random population sample of 100 observations, the calculated mean is 15.2 and standard deviation is 3.2. Calculate the 95% confidence interval for the expected value, then the 99% confidence interval. If the sample power and its variation remain unchanged and the confidence coefficient increases, will the confidence interval narrow or widen?

We substitute these values ​​into the expression for the confidence interval:

where is the critical value of the standard normal distribution for the significance level α = 0,05 .

We get:

.

Thus, the 95% confidence interval for the mean of this sample ranged from 14.57 to 15.82.

We again substitute these values ​​into the expression for the confidence interval:

where is the critical value of the standard normal distribution for the significance level α = 0,01 .

We get:

.

Thus, the 99% confidence interval for the mean of this sample ranged from 14.37 to 16.02.

As we see, as the confidence coefficient increases, the critical value of the standard normal distribution also increases, and, consequently, the starting and ending points of the interval are located further from the mean, and thus the confidence interval for the mathematical expectation increases.

Point and interval estimates of specific gravity

The share of some sample attribute can be interpreted as a point estimate of the share p of the same characteristic in the general population. If this value needs to be associated with probability, then the confidence interval of the specific gravity should be calculated p characteristic in the population with probability P = 1 - α :

.

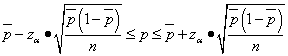Example 4. In some city there are two candidates A And B are running for mayor. 200 city residents were randomly surveyed, of which 46% responded that they would vote for the candidate A, 26% - for the candidate B and 28% do not know who they will vote for. Determine the 95% confidence interval for the proportion of city residents supporting the candidate A.

To begin with, let us recall the following definition:

Let's consider the following situation. Let the population variants have a normal distribution with mathematical expectation $a$ and standard deviation $\sigma$. The sample mean in this case will be considered as a random variable. When the quantity $X$ is normally distributed, the sample mean will also be normally distributed with the parameters

Let us find a confidence interval that covers the value $a$ with a reliability of $\gamma $.

To do this, we need the equality

From it we get

From here we can easily find $t$ from the table of function values ​​$Ф\left(t\right)$ and, as a consequence, find $\delta $.

Let us recall the table of values ​​of the function $Ф\left(t\right)$:

Figure 1. Table of function values ​​$Ф\left(t\right).$

Confidence integral for estimating the mathematical expectation for an unknown $(\mathbf \sigma )$

In this case, we will use the corrected variance value $S^2$. Replacing $\sigma $ with $S$ in the above formula, we get:

Example problems for finding a confidence interval

Example 1

Let the quantity $X$ have a normal distribution with variance $\sigma =4$. Let the sample size be $n=64$ and the reliability be $\gamma =0.95$. Find the confidence interval for estimating the mathematical expectation of this distribution.

We need to find the interval ($\overline(x)-\delta ,\overline(x)+\delta)$.

As we saw above

\[\delta =\frac(\sigma t)(\sqrt(n))=\frac(4t)(\sqrt(64))=\frac(\t)(2)\]

The parameter $t$ can be found from the formula

\[Ф\left(t\right)=\frac(\gamma )(2)=\frac(0.95)(2)=0.475\]

From Table 1 we find that $t=1.96$.