A házak területe a Fisher-kritérium. Fisher függvény az Excelben és példák a munkájára

Ebben a példában nézzük meg, hogyan becsüljük meg a kapott regressziós egyenlet megbízhatóságát. Ugyanezt a tesztet használjuk annak a hipotézisnek a tesztelésére, hogy a regressziós együtthatók egyaránt nullák, a=0, b=0. Vagyis a számítások lényege a kérdés megválaszolása: felhasználható-e további elemzésekre, előrejelzésekre?

Használja ezt a t-próbát a két minta eltérései közötti hasonlóság vagy különbség meghatározására.

Az elemzés célja tehát egy olyan becslés megszerzése, aminek segítségével megállapítható lenne, hogy az α bizonyos szintjén a kapott regressziós egyenlet statisztikailag megbízható. Ezért az R 2 determinációs együtthatót használjuk.
A regressziós modell szignifikanciájának ellenőrzése Fisher F-próbával történik, melynek számított értékét a vizsgált indikátor kezdeti megfigyelési sorozata szórásának és a reziduális sorozat varianciájának torzítatlan becslésének arányaként kapjuk meg. ezt a modellt.
Ha a k 1 =(m) és k 2 =(n-m-1) szabadságfokkal számított érték adott szignifikancia szinten nagyobb, mint a táblázatos érték, akkor a modell szignifikánsnak minősül.

ahol m a modellben szereplő tényezők száma.
Fokozat statisztikai jelentőség gőzszoba lineáris regresszió a következő algoritmus szerint készül:
1. Feltételezzük azt a nullhipotézist, hogy az egyenlet egésze statisztikailag jelentéktelen: H 0: R 2 =0 α szignifikancia szinten.
2. Ezután határozza meg az F-kritérium tényleges értékét:


ahol m=1 páronkénti regresszió esetén.
3. A táblázat értékét Fisher-eloszlási táblázatokból határozzuk meg egy adott szignifikanciaszintre, figyelembe véve, hogy a teljes négyzetösszeghez (nagyobb szóráshoz) a szabadságfok száma 1, a szabadságfokok száma pedig a maradék összegéhez. négyzetek (alacsonyabb variancia) a lineáris regresszióban n-2 (vagy via Excel funkció FDISP(valószínűség,1,n-2)).
Az F táblázat a kritérium maximális lehetséges értéke véletlenszerű tényezők hatására adott szabadsági fokra és α szignifikancia szintre. α szignifikancia szint - a helyes hipotézis elutasításának valószínűsége, feltéve, hogy igaz. Általában α értéke 0,05 vagy 0,01.
4. Ha az F-kritérium tényleges értéke kisebb, mint a táblázati érték, akkor azt mondják, hogy nincs ok a nullhipotézis elutasítására.
Ellenkező esetben a nullhipotézist elvetjük, és az egyenlet egészének statisztikai szignifikanciájáról szóló alternatív hipotézist (1-α) valószínűséggel elfogadjuk.
A k 1 =1 és k 2 =48 szabadságfokkal rendelkező kritérium táblázati értéke, F táblázat = 4

következtetéseket: Mivel az F > F táblázat tényleges értéke, a determinációs együttható statisztikailag szignifikáns ( a regressziós egyenlet talált becslése statisztikailag megbízható) .

Varianciaanalízis

.

A regressziós egyenlet minőségi mutatói

Példa. Összesen 25 kereskedelmi vállalkozás alapján vizsgálják a jelek közötti kapcsolatot: X - A áruk ára, ezer rubel; Y - profit kereskedelmi vállalkozás, millió rubel A regressziós modell értékelésekor a következő köztes eredményeket kaptuk: ∑(y i -y x) 2 = 46000; ∑(y i -y sr) 2 = 138000. Milyen korrelációs mutató határozható meg ezekből az adatokból? Számítsa ki ennek a mutatónak az értékét az eredmény alapján és felhasználásával Fisher F-teszt következtetést levonni a regressziós modell minőségéről.
Megoldás. Ezen adatok alapján empirikus összefüggés állapítható meg: , ahol ∑(y cf -y x) 2 = ∑(y i -y cf) 2 - ∑(y i -y x) 2 = 138000 - 46000 = 92 000.
η 2 = 92000/138000 = 0,67, η = 0,816 (0,7< η < 0.9 - связь между X и Y высокая).

Fisher F-teszt n = 25, m = 1.
R 2 = 1 - 46000 / 138000 \u003d 0,67, F = 0,67 / (1-0,67)x (25 - 1 - 1) \u003d 46. F táblázat (1; 23) \u003d \u003d
Mivel F > Ftabl tényleges értéke, a regressziós egyenlet talált becslése statisztikailag megbízható.

Kérdés: Milyen statisztikát használunk egy regressziós modell szignifikanciájának tesztelésére?
Válasz: A teljes modell egészének jelentőségéhez F-statisztikát (Fisher-kritérium) használunk.

A FISHER függvény az X argumentumok Fisher-transzformációját adja vissza. Ez a transzformáció olyan függvényt épít fel, amelynek normális, nem pedig aszimmetrikus eloszlása ​​van. A FISHER függvény a hipotézis tesztelésére szolgál a korrelációs együttható segítségével.

A FISHER függvény leírása Excelben

Amikor ezzel a függvénnyel dolgozik, be kell állítania a változó értékét. Azonnal meg kell jegyezni, hogy vannak olyan helyzetek, amikor ez a funkció nem hoz eredményt. Ez akkor lehetséges, ha a változó:

• nem szám. Ilyen helyzetben a FISHER függvény az #ÉRTÉK hibaértéket adja vissza;
• vagy kisebb, mint -1, vagy nagyobb, mint 1. Ebben az esetben a FISHER függvény a #NUM! hibaértéket adja vissza.

A FISHER függvény matematikai leírására használt egyenlet a következő:

Z"=1/2*ln(1+x)/(1-x)

Tekintsük ennek a függvénynek az alkalmazását 3 konkrét példán.



A nyereség és a költségek kapcsolatának értékelése FISHER függvény segítségével

1. példa Kereskedelmi szervezetek tevékenységére vonatkozó adatok felhasználásával fel kell mérni az Y nyereség (millió rubel) és a termékek fejlesztéséhez felhasznált X költségek (millió rubel) közötti összefüggést (az 1. táblázatban látható).

1. táblázat – Kiindulási adatok:

№	x	Y
1	210 000 000,00 RUB	95 000 000,00 USD
2	1 068 000 000,00 RUB	76 000 000,00 RUB
3	1 005 000 000,00 RUB	78 000 000,00 RUB
4	610 000 000,00 RUB	89 000 000,00 RUB
5	768 000 000,00 RUB	77 000 000,00 RUB
6	799 000 000,00 RUB	85 000 000,00 RUB

Az ilyen problémák megoldásának sémája a következő:

1. Számított lineáris együtthatóösszefüggések r xy ;
2. A lineáris korrelációs együttható jelentőségét Student-féle t-próba alapján ellenőrizzük. Ezzel egyidejűleg felterjesztjük és teszteljük azt a hipotézist, hogy a korrelációs együttható nullával egyenlő. Ennek a hipotézisnek a tesztelésekor a t-statisztikát használjuk. Ha a hipotézis beigazolódik, a t-statisztika Student-féle eloszlású. Ha a számított érték t p > t cr, akkor a hipotézist elvetjük, ami a lineáris korrelációs együttható szignifikanciáját, következésképpen az X és Y közötti kapcsolat statisztikai szignifikanciáját jelzi;
3. Meghatározzuk a statisztikailag szignifikáns lineáris korrelációs együttható intervallumbecslését.
4. A lineáris korrelációs együttható intervallumbecslését a alapján határozzuk meg inverz z-transzformáció Halász;
5. Kiszámítjuk a lineáris korrelációs együttható standard hibáját.

A probléma megoldásának eredményeit az Excel csomagban használt függvényekkel az 1. ábra mutatja.

1. ábra - Példa számításokra.

sz. p / p	Az indikátor neve	Számítási képlet
1	Korrelációs együttható	=CORREL(B2:B7;C2:C7)
2	A t-kritérium becsült értéke tp	=ABS(C8)/ROOT(1-POWER(C8,2))*GYÖKÉR(6-2)
3	A t-próba trh táblázati értéke	=STUDISP(0,05;4)
4	A szabvány táblázati értéke normális eloszlás zy	=NORMINV((0,95+1)/2)
5	Fischer transzformációs érték z'	=HALÁSZ(C8)
6	Bal intervallum becslése z-re	=C12-C11*GYÖKÉR(1/(6-3))
7	Jobb intervallumbecslés z-re	=C12+C11*GYÖKÉR(1/(6-3))
8	Bal oldali intervallumbecslés az rxy-hez	=FISCHEROBR(C13)
9	Az rx megfelelő intervallumbecslése	=FISCHEROBR(C14)
10	Az rxy szórása	=GYÖKÉR((1-C8^2)/4)

Így 0,95 valószínűséggel a lineáris korrelációs együttható (–0,386) és (–0,990) közötti tartományba esik. standard hiba 0,205.

Az FDISP függvény regressziójának statisztikai szignifikanciájának ellenőrzése

2. példa Ellenőrizze az egyenlet statisztikai szignifikanciáját többszörös regresszió Fisher-féle F-próba segítségével vonjon le következtetéseket.

Az egyenlet egészének szignifikanciájának tesztelésére feltesszük a H 0 hipotézist a determinációs együttható statisztikai jelentéktelenségéről és ezzel ellentétes H 1 hipotézist a determinációs együttható statisztikai szignifikanciájáról:

H 1: R 2 ≠ 0.

Teszteljük a hipotéziseket Fisher-féle F-próbával. A mutatókat a 2. táblázat tartalmazza.

2. táblázat – Kiindulási adatok

Ehhez az alábbi függvényt használjuk az Excel csomagban:

FDISP(α;p;n-p-1)

• α az adott eloszláshoz tartozó valószínűség;
• p és n a szabadsági fokok számlálója, illetve nevezője.

Tudva, hogy α = 0,05, p = 2 és n = 53, a következő értéket kapjuk F crit-re (lásd 2. ábra).

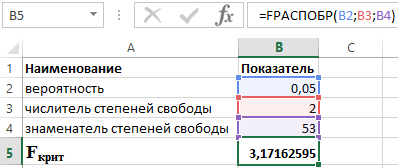
2. ábra - Példa számításokra.

Így azt mondhatjuk, hogy F calc > F crit. Ennek eredményeként a determinációs együttható statisztikai szignifikanciájára vonatkozó H 1 hipotézist elfogadjuk.

A korrelációs mutató értékének kiszámítása Excelben

3. példa: 23 vállalkozás adatainak felhasználása a következőkről: X - az A termék ára, ezer rubel; Y - egy kereskedelmi vállalkozás nyeresége, millió rubel, a függőségüket vizsgálják. A regressziós modell értékelése a következőket adta: ∑(yi-yx) 2 = 50000; ∑(yi-yср) 2 = 130000. Milyen korrelációs mutató határozható meg ezekből az adatokból? Számítsa ki a korrelációs index értékét, és a Fisher-teszt segítségével vonjon le következtetést a regressziós modell minőségére vonatkozóan!

Határozzuk meg az F crit kifejezést:

F számolt = R 2 / 23 * (1-R 2)

ahol R a determinációs együttható 0,67.

Így a számított érték F calc = 46.

Az F-kritérium meghatározásához a Fisher-eloszlást használjuk (lásd a 3. ábrát).

3. ábra - Példa számításokra.

Így a regressziós egyenlet kapott becslése megbízható.

Fisher-kritérium

A Fisher-kritérium a két általános sokaság varianciáinak egyenlőségére vonatkozó hipotézis tesztelésére szolgál, normál törvény szerint eloszolva. Ez egy parametrikus kritérium.

A Fisher-féle F-próbát varianciahányadosnak nevezzük, mivel két összehasonlított torzítatlan varianciabecslés arányaként jön létre.

Legyen két minta a megfigyelések eredményeként. Ezek alapján az eltérések ill amelynek És szabadsági fokokat. Feltételezzük, hogy az első mintát az általános sokaságból vettük szórással , a második pedig az általános populációból egy eltéréssel . A nullhipotézist a két variancia egyenlőségéről terjesztik elő, azaz. H0:
vagy . Ennek a hipotézisnek az elvetéséhez igazolni kell a különbség szignifikanciáját egy adott szignifikanciaszinten.
.

A kritérium értékét a következő képlettel számítjuk ki:

Nyilvánvaló, hogy ha az eltérések egyenlőek, akkor a kritérium értéke eggyel lesz egyenlő. Más esetekben nagyobb (kevesebb) lesz egynél.

A kritériumnak Fisher-eloszlása ​​van
. A Fisher-teszt egy kétirányú teszt, és a nullhipotézis
alternatíva javára elutasították
Ha . Itt hol
az első és a második minta térfogata.

A STATISTICA rendszer egyirányú Fisher tesztet valósít meg, azaz. mint mindig, a maximális szórással. Ebben az esetben a nullhipotézist elvetjük az alternatíva javára, ha .

Példa

Tűzzük ki a feladatot, hogy összehasonlítsuk két tanulócsoport képzésének eredményességét. Az előrehaladás szintje a tanulási folyamat irányításának szintjét, a szóródás pedig a tanulásmenedzsment minőségét, a tanulási folyamat szervezettségi fokát jellemzi. Mindkét mutató független és általános eset közösen kell mérlegelni. Az egyes tanulócsoportok előmeneteli szintjét (matematikai elvárásait) a számtani átlag jellemzi és , a minőséget pedig a becslések megfelelő mintavarianciái jellemzik: és . A jelenlegi teljesítmény szintjének értékelése során kiderült, hogy mindkét hallgató esetében ugyanaz: == 4,0. Minta eltérések:
És
. Az ezeknek a becsléseknek megfelelő szabadsági fokok száma:
És
. Ennélfogva a képzés hatékonyságában mutatkozó különbségek megállapításához felhasználhatjuk a tanulmányi teljesítmény stabilitását, pl. teszteljük a hipotézist.

Kiszámít
(a számlálónak nagy szórással kell rendelkeznie), . A táblázatok szerint ( STATISZTIKA – Valószínűségterjesztésszámológép) azt találjuk, ami kisebb a számítottnál, ezért a nullhipotézist el kell utasítani az alternatíva javára. Ez a következtetés nem biztos, hogy kielégíti a kutatót, hiszen az arány valódi értéke érdekli
(a számlálóban mindig nagy a szórás). Egyoldalú feltétel ellenőrzésekor , ami kisebb a fent számolt értéknél. Tehát a nullhipotézist el kell utasítani az alternatíva javára.

Fisher-teszt a STATISTICA programban Windows környezetben

Példaként egy hipotézis tesztelésére (Fisher-kritérium) használunk (hozzunk létre) egy fájlt két változóval (fisher.sta):

Rizs. 1. Táblázat két független változóval

A hipotézis teszteléséhez az alapstatisztikában szükséges ( AlapvetőStatisztikaéstáblázatok) válassza a Student-féle tesztet a független változókhoz. ( t-próba, független, változók szerint).

Rizs. 2. Paraméteres hipotézisek tesztelése

A változók kiválasztása és a gomb megnyomása után Összegzés a szórások értékeit és a Fisher-tesztet számítják ki. Ezenkívül meghatározzák a szignifikancia szintjét p, ahol a különbség jelentéktelen.

Rizs. 3. A hipotézis tesztelésének eredményei (F-próba)

Használata Valószínűségszámológép a paraméterek értékének beállításával pedig a számított érték jelölésével ábrázolhatjuk a Fisher-eloszlást.

Rizs. 4. A hipotézis elfogadásának (elutasításának) területe (F-kritérium)

Források.

Hipotézisek tesztelése két variancia kapcsolatáról

URL: /tryphonov3/terms3/testdi.htm

6. előadás :8080/resources/math/mop/lections/lection_6.htm

F – Fisher-kritérium

URL: /home/portal/applications/Multivariatadvisor/F-Fisheer/F-Fisheer.htm

Valószínűségi és statisztikai kutatás elmélete és gyakorlata.

URL: /active/referats/read/doc-3663-1.html

F – Fisher-kritérium

Fisher-kritérium lehetővé teszi két független minta mintavarianciáinak összehasonlítását. Az F emp kiszámításához meg kell találni két minta szórásának arányát, és úgy, hogy a nagyobb szórás a számlálóban, a kisebb pedig a nevezőben legyen. A Fisher-kritérium kiszámításának képlete a következő:

ahol az első és a második minta szórása.

Mivel a kritérium feltétele szerint a számláló értékének nagyobbnak vagy egyenlőnek kell lennie a nevező értékével, a Fem értéke mindig nagyobb vagy egyenlő, mint egy.

A szabadsági fokok számát is egyszerűen meghatározzuk:

k 1 =n l - 1 az első mintára (vagyis a nagyobb szórással rendelkező mintára) és k 2 = n 2 - 1 a második mintához.

Az 1. függelékben a Fisher-kritérium kritikus értékeit a k 1 (a táblázat felső sora) és a k 2 (a táblázat bal oszlopa) értékek határozzák meg.

Ha t emp >t crit, akkor a nullhipotézist elfogadjuk, ellenkező esetben az alternatívát.

3. példa A tesztelést két harmadik osztályban végezték el mentális fejlődés tíz diák TURMSh tesztje szerint. A kapott átlagértékek nem különböztek szignifikánsan, azonban a pszichológust érdekli a kérdés - vannak-e különbségek a mentális fejlődési mutatók homogenitásának mértékében az osztályok között.

Megoldás. A Fisher-kritériumhoz össze kell hasonlítani a teszteredmények szórását mindkét osztályban. A teszt eredményeit a táblázat tartalmazza:

3. táblázat

tanulók száma	Első osztályú	Másodosztály

Az X és Y változók szórásainak kiszámítása után a következőket kapjuk:

s x 2 =572,83; s y 2 =174,04

Ekkor az F Fisher-kritérium szerinti számításhoz a (8) képlet szerint a következőket kapjuk:

Az 1. függelék táblázata szerint az F kritériumhoz, ahol a szabadságfok mindkét esetben egyenlő k=10 - 1 = 9, F crit = 3,18 (<3.29), следовательно, в терминах статистических гипотез можно утвер­ждать, что Н 0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н 1 . Иcследователь может утверждать, что по степени однородности такого показа­теля, как умственное развитие, имеется различие между выбор­ками из двух классов.

6.2 Nem paraméteres tesztek

Az expozíció előtti és utáni eredményeket szemmel (százalékosan) összehasonlítva a kutató arra a következtetésre jut, hogy ha eltérések figyelhetők meg, akkor különbség van az összehasonlított mintákban. Egy ilyen megközelítés kategorikusan elfogadhatatlan, mivel lehetetlen meghatározni a százalékos eltérések megbízhatósági szintjét. Az önmagukban vett százalékok nem teszik lehetővé statisztikailag megbízható következtetések levonását. Bármely hatás hatékonyságának bizonyításához meg kell határozni egy statisztikailag szignifikáns tendenciát az indikátorok eltolódásában (eltolódásában). Az ilyen problémák megoldásához a kutató számos különbségi kritériumot használhat. Az alábbiakban nem paraméteres teszteket veszünk figyelembe: az előjelpróbát és a khi-négyzet tesztet.

)

A φ* kritérium kiszámítása

1. Határozza meg az attribútum azon értékeit, amelyek alapján az alanyokat „hatással” és „nincs hatással” valókra osztjuk. Ha a tulajdonság számszerűsített, használja a λ kritériumot az optimális hasadási pont megtalálásához.

2. Rajzoljon egy négycellás (szinonimája: négymezős) táblázatot két oszlopból és két sorból! Az első oszlop a „hatás van”; a második oszlop a „nincs hatás”; első sor felülről - 1 csoport (minta); a második sor - 2 csoport (minta).

4. Számolja meg az első mintában szereplő alanyok számát, akiknek nincs hatása, és írja be ezt a számot a táblázat jobb felső cellájába. Számítsa ki a felső két cella összegét! Meg kell egyeznie az első csoport tantárgyainak számával.

6. Számolja meg a második minta azon alanyainak számát, akiknek nincs hatása, és írja be ezt a számot a táblázat jobb alsó cellájába. Számítsa ki a két alsó cella összegét! Meg kell egyeznie a második csoport (minta) alanyainak számával.

7. Határozza meg azoknak az alanyoknak a százalékos arányát, akiknek "hatásuk van" úgy, hogy számukat az ebben a csoportban (mintában) lévő alanyok számához viszonyítja. A kapott százalékos értékeket a táblázat bal felső és bal alsó cellájába írjuk be zárójelben, hogy ne keverjük össze az abszolút értékekkel.

8. Ellenőrizze, hogy az egyező százalékok egyike egyenlő-e nullával. Ha ez a helyzet, próbáljon meg változtatni ezen úgy, hogy a csoportok felosztási pontját az egyik vagy a másik oldalra mozgatja. Ha ez lehetetlen vagy nemkívánatos, dobja el a φ* kritériumot, és használja a χ2 kritériumot.

9. Határozza meg a táblázat szerint. XII. 1. melléklet a φ szögek értékeit minden egyes összehasonlított százalékra.

ahol: φ1 - a nagyobb százaléknak megfelelő szög;

φ2 - kisebb százaléknak megfelelő szög;

N1 - megfigyelések száma az 1. mintában;

N2 - megfigyelések száma a 2. mintában.

11. Hasonlítsa össze a kapott φ* értéket a kritikus értékekkel: φ* ≤1,64 (р<0,05) и φ* ≤2,31 (р<0,01).

Ha φ*emp ≤φ*cr. H0 elutasítva.

Ha szükséges, határozza meg a kapott φ*emp pontos szignifikanciaszintjét a táblázat szerint. XIII 1. függelék.

Ezt a módszert számos kézikönyv leírja (Plokhinsky N.A., 1970; Gubler E.V., 1978; Ivanter E.V., Korosov A.V., 1992 stb.). Ez a leírás a módszer E.V. által kidolgozott és bemutatott verzióján alapul. Gubler.

A kritérium célja φ*

A Fisher-teszt célja két minta összehasonlítása a kutatót érdeklő hatás (indikátor) előfordulási gyakorisága szerint. Minél nagyobb, annál megbízhatóbbak a különbségek.

A kritérium leírása

A kritérium két minta azon százalékai közötti különbségek megbízhatóságát értékeli, amelyekben a számunkra érdekes hatás (indikátor) regisztrálva van. Képletesen szólva a 2 lepényből kivágott 2 legjobb darabot összehasonlítjuk egymással, és eldöntjük, melyik a nagyobb igazán.

A Fisher-szögtranszformáció lényege a százalékok középszögekké alakítása, amelyeket radiánban mérünk. Nagyobb százalék nagyobb φ szögnek, kisebb százalék kisebb szögnek felel meg, de az összefüggések itt nem lineárisak:

ahol P az egység törtrészében kifejezett százalék (lásd 5.1. ábra).

A φ szögek közötti eltérés növekedésével 1 és φ 2 és a minták számának növekedésével a kritérium értéke nő. Minél nagyobb a φ* érték, annál valószínűbb, hogy a különbségek jelentősek.

Hipotézisek

H 0 : Személyek aránya, amelyek a vizsgált hatást mutatják meg, az 1. mintában legfeljebb a 2. mintában.

H 1 : A vizsgált hatást mutató emberek aránya nagyobb az 1. mintában, mint a 2. mintában.

Egy kritérium grafikus ábrázolása φ*

A szögtranszformációs módszer valamivel elvontabb, mint a többi kritérium.

A képlet, amelyhez E. V. Gubler ragaszkodik a φ értékeinek kiszámításakor, feltételezi, hogy a 100% a φ=3,142 szög, azaz a π=3,14159 kerekített érték... Ez lehetővé teszi, hogy az összehasonlított mintákat a következő formában ábrázoljuk. két félkör, amelyek mindegyike a mintájuk számának 100%-át szimbolizálja. A „hatással” rendelkező alanyok százalékos aránya a φ központi szögek által alkotott szektorokként jelenik meg. ábrán Az 5.2. ábra az 1. példát szemléltető két félkört mutat be. Az első mintában az alanyok 60%-a oldotta meg a feladatot. Ez a százalék a φ=1,772 szögnek felel meg. A második mintában az alanyok 40%-a oldotta meg a problémát. Ez a százalék a φ =1,369 szögnek felel meg.

A φ* kritérium lehetővé teszi annak meghatározását, hogy adott mintaméretek esetén az egyik szög statisztikailag szignifikánsan jobb-e a másiknál.

Kritériumi korlátozások φ*

1. Az összehasonlított részesedések egyike sem lehet egyenlő nullával. Formálisan nincs akadálya a φ módszer alkalmazásának olyan esetekben, amikor a megfigyelések aránya valamelyik mintában 0. Ezekben az esetekben azonban indokolatlanul magas lehet az eredmény (Gubler E.V., 1978, 86. o.) .

2. Felső a φ kritériumban nincs határ - a minták tetszőlegesen nagyok lehetnek.

Alsó a határ 2 megfigyelés az egyik mintában. A két minta méretében azonban a következő arányokat kell betartani:

a) ha egy mintában csak 2 megfigyelés van, akkor a másodiknak legalább 30-nak kell lennie:

b) ha az egyik mintában csak 3 megfigyelés van, akkor a másodiknak legalább 7-nek kell lennie:

c) ha az egyik mintában csak 4 megfigyelés van, akkor a másodiknak legalább 5-nek kell lennie:

d) atn 1 , n 2 ≥ 5 bármilyen összehasonlítás lehetséges.

Elvileg olyan mintákat is össze lehet hasonlítani, amelyek nem felelnek meg ennek a feltételnek, például a relációvaln 1 =2, n 2 = 15, de ezekben az esetekben nem lehet jelentős eltéréseket kimutatni.

A φ* kritériumnak nincs más megkötése.

Nézzünk néhány példát a lehetőségek illusztrálásáraφ* kritérium.

1. példa: minták összehasonlítása egy minőségileg meghatározott jellemző szerint.

2. példa: minták összehasonlítása egy mennyiségileg mért tulajdonság szerint.

3. példa: a minták összehasonlítása egy jellemző szintje és eloszlása ​​szempontjából.

4. példa: a φ* kritérium használata a feltétellel kombinálvax Kolmogorov-Smirnov a legpontosabb eredmény elérése érdekében.

1. példa - minták összehasonlítása egy minőségileg meghatározott jellemző szerint

A teszt ezen felhasználása során összehasonlítjuk az egyik mintában bizonyos minőséggel jellemezhető alanyok százalékos arányát egy másik mintában az azonos minőséggel jellemezhető alanyok százalékos arányával.

Tegyük fel, hogy az érdekel minket, hogy a tanulók két csoportja különbözik-e egy új kísérleti probléma megoldásának sikerében. Az első 20 fős csoportban 12 fő birkózott meg vele, a második 25 fős mintában 10. Az első esetben a problémát megoldók aránya 12/20 100% = 60%, ill. a másodikban 10/25 100% = 40%. Ezek a százalékok jelentősen eltérnek-e az adatoktóln 1 Ésn 2 ?

Úgy tűnik, hogy "szemmel" megállapítható, hogy a 60% sokkal magasabb, mint a 40%. Ezek a különbségek azonban valójábann 1 , n 2 megbízhatatlan.

Nézzük meg. Mivel minket a probléma megoldásának ténye érdekel, a kísérleti probléma megoldásának sikerét „hatásnak”, a megoldási kudarcot pedig hatás hiányának fogjuk tekinteni.

Fogalmazzuk meg a hipotéziseket.

H 0 : Személyek arányamegbirkózott a feladattal, az első csoportban nem több, mint a második csoportban.

H 1 : Az első csoportban nagyobb azoknak az aránya, akik megbirkóztak a feladattal, mint a második csoportban.

Most készítsük el az úgynevezett négycellás vagy négymezős táblát, ami tulajdonképpen egy empirikus gyakorisági táblázat két attribútumértékhez: "hatás van" - "nincs hatás".

5.1. táblázat

Négycellás táblázat a kritérium kiszámításához, amikor két alanycsoportot hasonlítanak össze a problémát megoldók százalékos arányával.

Csoportok	"Van hatás": a feladat megoldva			"Nincs hatás": a probléma nincs megoldva			Összegek
	Mennyiség tesztalanyok	% Ossza meg		Mennyiség tesztalanyok	% Ossza meg
1 csoport		(60%)			(40%)
2 csoport		(40%)			(60%)
Összegek

A négycellás táblázatban általában a "Van hatás" és a "Nincs hatás" oszlopok felül vannak jelölve, a "Group 1" és a "Group 2" sorok pedig a bal oldalon vannak. Valójában csak az A és B mezők (cellák) vesznek részt az összehasonlításban, vagyis a „Van hatás” oszlopban lévő százalékok.

táblázat szerint.XIIAz 1. függelék meghatározza a φ értékeit, amelyek megfelelnek az egyes csoportok százalékos arányának.

Most számítsuk ki φ* tapasztalati értékét a képlet segítségével:

ahol φ 1 - a nagyobb %-os részesedésnek megfelelő szög;

φ 2 - a kisebb %-os részesedésnek megfelelő szög;

n 1 - megfigyelések száma az 1. mintában;

n 2 - a megfigyelések száma a mintában 2.

Ebben az esetben:

táblázat szerint.XIIIAz 1. függelék határozza meg, hogy milyen szignifikanciaszint felel meg φ* emp=1,34:

p=0,09

A pszichológiában elfogadott statisztikai szignifikanciaszinteknek megfelelő φ* kritikus értékei is megállapíthatók:

Építsünk egy „jelentősségi tengelyt”.

A kapott φ* tapasztalati érték a jelentéktelenség zónájában van.

Válasz: H 0 elfogadott. A feladatot teljesítők arányaVaz első csoport nem több, mint a második csoport.

Csak szimpatizálni lehet azzal a kutatóval, aki 20%-os, sőt 10%-os szignifikáns különbségeket is figyelembe vesz anélkül, hogy a φ*-kritérium alapján ellenőrizné azok megbízhatóságát. Ebben az esetben például csak legalább 24,3%-os eltérések lennének szignifikánsak.

Úgy tűnik, hogy ha két mintát valamilyen minőségi kritérium alapján hasonlítunk össze, akkor a φ kritérium inkább idegesít, mintsem örömet okoz. Ami statisztikai szempontból jelentősnek tűnt, nem biztos, hogy az.

Sokkal több lehetőség nyílik a kutató kedvére a Fisher-kritériumnál, ha két mintát kvantitatívan mért tulajdonságok alapján hasonlítunk össze, és variálhatjuk a „hatást.

2. példa - két minta összehasonlítása egy mennyiségileg mért tulajdonság szerint

A kritérium alkalmazásának ebben a változatában összehasonlítjuk azon alanyok százalékos arányát az egyik mintában, akik egy adott tulajdonságérték bizonyos szintjét elérik, és azon alanyok százalékos arányát, akik egy másik mintában elérik ezt a szintet.

G. A. Tlegenova (1990) vizsgálatában a szakiskolákban tanuló 70, 14 és 16 év közötti fiatal férfi közül 10 olyan alanyt választottak ki, akik az Agresszivitás skálán magas pontszámot értek el, és 11 alanyt, akik alacsony pontszámot értek el az Agresszió skálán a Freiburgi Személyiség Kérdőív segítségével végzett felmérés eredményei. Meg kell határozni, hogy az agresszív és nem agresszív fiatal férfiak csoportjai különböznek-e abban a távolságban, amelyet spontán választanak egy diáktárssal folytatott beszélgetés során. G. A. Tlegenova adatait a táblázat tartalmazza. 5.2. Látható, hogy az agresszív fiatal férfiak gyakrabban választják az 50-es távolságotcm vagy még kevesebb, míg a nem agresszív fiatalok nagyobb valószínűséggel választanak 50 cm-nél nagyobb távolságot.

Most az 50 cm-es távolságot tekinthetjük kritikusnak, és úgy tekinthetjük, hogy ha az alany által választott távolság kisebb vagy egyenlő, mint 50 cm, akkor van "hatás", és ha a választott távolság nagyobb, mint 50 cm, akkor nincs hatása. Azt látjuk, hogy az agresszív fiatal férfiak csoportjában 10-ből 7-ben, azaz az esetek 70%-ában, a nem agresszív fiatalok csoportjában pedig 11-ből 2-ben, azaz 18,2-ben figyelhető meg a hatás. az esetek %-a. Ezek a százalékok a φ* módszerrel összehasonlíthatók a köztük lévő különbségek érvényességének megállapítására.

5.2. táblázat

Az agresszív és nem agresszív fiatal férfiak által választott távolság mutatói (cm-ben) egy diáktársával folytatott beszélgetés során (G.A. Tlegenova, 1990 szerint)

	1. csoport: az Agresszivitás skálán magas pontszámot elért fiúkFPI- R (n 1 =10)		2. csoport: fiúk alacsony pontszámmal az Agresszivitás skálánFPI- R (n 2 =11)
	d(c m )	% Ossza meg	d(c M )	% Ossza meg
"Eszik Hatás" d≤50 cm
				18,2%
"Nem hatás" d>50 cm
	80 QO			81,8%
Összegek		100%		100%
Közepes	5b:o		77.3

Fogalmazzuk meg a hipotéziseket.

H 0 d ≤ 50 lásd, nincs agresszívabb fiú a csoportban, mint a nem agresszív fiúk csoportjában.

H 1 : A távolságot választók arányad≤ 50 cm, az agresszív fiúk csoportjában több, mint a nem agresszív fiúk csoportjában. Most készítsük el az úgynevezett négycellás táblát.

53. táblázat

Egy négycellás táblázat a φ*-kritérium kiszámításához az agresszív csoportok összehasonlításakornf=10) és nem agresszív fiúk (n2=11)

Csoportok	"Van hatás": d≤50			"Hatástalan." d>50			Összegek
	A tesztalanyok száma	(% Ossza meg)		A tesztalanyok száma	(% Ossza meg)
1. csoport - agresszív fiúk		(70%)			(30%)
2. csoport - nem agresszív fiúk		(180%)			(81,8%)
Összeg

táblázat szerint.XIIAz 1. függelék meghatározza a φ értékeit, amelyek megfelelnek a „hatás” százalékos arányának az egyes csoportokban.

A kapott φ* tapasztalati érték a szignifikancia zónában van.

Válasz: H 0 elutasítva. elfogadottH 1 . Az agresszív fiúk csoportjában nagyobb azoknak az aránya, akik a beszélgetés során 50 cm-nél kisebb távolságot választanak, mint a nem agresszív fiúk csoportjában.

A kapott eredmény alapján arra a következtetésre juthatunk, hogy az agresszívebb fiúk gyakrabban választanak fél méternél kisebb, míg a nem agresszív fiúk gyakrabban fél méternél nagyobb távolságot. Azt látjuk, hogy az agresszív fiatal férfiak valójában az intim (0-46 cm) és a személyes zóna (46 cm-től) határán kommunikálnak. Emlékezzünk azonban arra, hogy a partnerek közötti bensőséges távolság nem csak a szoros jó kapcsolatok kiváltsága, hanemÉskézi harc (előszobaE. T., 1959).

3. példa – a minták összehasonlítása a jellemzők szintje és eloszlása ​​szempontjából.

A teszt alkalmazásának ebben a változatában először ellenőrizhetjük, hogy a csoportok eltérnek-e valamely tulajdonság szintjében, majd összehasonlíthatjuk a tulajdonság eloszlását két mintában. Egy ilyen feladat releváns lehet az alanyok által valamilyen új módszerrel kapott becslések tartományaiban vagy eloszlási formái közötti különbségek elemzésében.

R. T. Chirkina (1995) tanulmányában használtak először kérdőívet, amelynek célja a tények, nevek, szándékok és cselekvési módszerek kiszorítására való hajlam azonosítása volt az emlékezetből személyes, családi és szakmai komplexusok miatt. A kérdőív E. V. Sidorenko részvételével készült a 3. Freud "A mindennapi élet pszichopatológiája" című könyv anyagai alapján. A Pedagógiai Intézet 50 fős, nőtlen, gyermektelen, 17 és 20 év közötti hallgatói mintáját vizsgáltuk ezzel a kérdőívvel, valamint Menester-Corzini technikával a saját elégtelenség érzésének intenzitásának meghatározására.vagy"kisebbrendűségi komplexus"mesterG. J., CorsiniR. J., 1982).

A felmérés eredményeit a táblázat tartalmazza. 5.4.

Érvelhető-e, hogy van-e szignifikáns összefüggés a kérdőív segítségével diagnosztizált elmozdulási energia mutatója és az intenzitás, a saját elégtelenség érzése között?

5.4. táblázat

A saját elégtelenség érzésének intenzitásának mutatói magas (nj=18) és alacsony (n2=24) elmozdulási energia

1. csoport: elmozdulási energia 19 pontról 31 pontra (n 1 =181		2. csoport: elmozdulási energia 7 és 13 pont között (n 2 =24)
0; 0; 0; 0; 0 20; 20 30; 30; 30; 30; 30; 30; 30 50; 50 60; 60		0; 0 5; 5; 5; 5 10; 10; 10; 10; 10; 10 15; 15 20; 20; 20; 20 30; 30; 30; 30; 30; 30
Összegek Közepes	26,11	15,42

Annak ellenére, hogy az erőteljesebb elmozdulású csoport átlagértéke magasabb, 5 nulla érték is megfigyelhető benne. Ha összehasonlítjuk a becslések eloszlásának hisztogramjait két mintában, akkor szembetűnő kontrasztot találunk közöttük (5.3. ábra).

Két eloszlás összehasonlításához alkalmazhatjuk a kritériumotχ 2 vagy kritériumλ , de ehhez a számjegyeket kellene felnagyítanunk, ráadásul mindkét mintábann <30.

A φ* kritérium lehetővé teszi, hogy ellenőrizzük a grafikonon megfigyelt két eloszlás közötti eltérés hatását, ha egyetértünk azzal, hogy úgy tekintjük, hogy van "hatás", ha az elégtelenség mutatója nagyon alacsonyra (0) kerül. vagy fordítva, nagyon magas értékek (S30), és nincs hatás, ha a hiánypont a középső tartományban, 5 és 25 között van.

Fogalmazzuk meg a hipotéziseket.

H 0 : Az elégtelenségi index szélső értékei (0 vagy 30 vagy több) az erőteljesebb represszióval rendelkező csoportban nem gyakoribbak, mint a kevésbé erőteljes repressziós csoportban.

H 1 : Az elégtelenségi index extrém értékei (0 vagy 30 vagy több) az erőteljesebb elnyomással járó csoportban gyakoribbak, mint a kevésbé erőteljes represszióval rendelkező csoportokban.

Hozzunk létre egy négycellás táblázatot, amely kényelmes a φ* kritérium további kiszámításához.

5.5. táblázat

Négycellás táblázat a φ*-kritérium kiszámításához nagyobb és kisebb elmozdulási energiájú csoportok összehasonlításakor az elégtelenségi mutatók aránya szerint

Csoportok	"Hatékony": a hiánypontszám 0 vagy >30		„Nincs hatás”: hiánypontszám 5-től 25-ig		Összegek
		(88,9%)		(11,1%)
		(33,3%)		(66,7%)
Összegek

táblázat szerint.XIIAz 1. függelékben meghatározzuk az összehasonlított százalékoknak megfelelő φ értékeit:

Számítsuk ki φ* tapasztalati értékét:

φ* kritikus értékei bármelyn 1 , n 2 , mint az előző példából emlékszünk, a következők:

Tab.XIIIAz 1. függelék lehetővé teszi a kapott eredmény szignifikanciaszintjének pontosabb meghatározását: p<0,001.

Válasz: H 0 elutasítva. elfogadottH 1 . Az elégtelenségi index szélső értékei (0 vagy 30 vagy több) a nagyobb elmozdulási energiájú csoportban gyakoribbak, mint az alacsonyabb elmozdulási energiájú csoportban.

Tehát a magasabb elfojtási energiával rendelkező alanyok nagyon magas (30 vagy több) és nagyon alacsony (nulla) mutatókkal is rendelkezhetnek saját elégtelenségük érzésére. Feltételezhető, hogy mind az elégedetlenségüket, mind a siker iránti igényüket elfojtják. Ezek a feltételezések további ellenőrzést igényelnek.

A kapott eredmény értelmezésétől függetlenül megerősíti a φ*-kritérium lehetőségét a tulajdonságok eloszlásának formáiban mutatkozó különbségek értékelésében két mintában.

Az eredeti mintában 50 fő szerepelt, de közülük 8 főt kizártak a számításból, mivel az elmozdulás anergiája mutatója átlagos pontszáma (14-15). Az elégtelenség érzésének intenzitásának mutatói is átlagosak: 6 20 pontos érték és 2 25 pontos érték.

A φ*-kritérium erőteljes lehetőségeit egy teljesen más hipotézis megerősítésével láthatjuk a példa anyagainak elemzésekor. Bebizonyíthatjuk például, hogy egy magasabb elfojtási energiájú csoportban a hiánymutató még mindig magasabb, annak ellenére, hogy ebben a csoportban paradoxon megoszlik.

Állítsunk fel új hipotéziseket.

H 0 Az elégtelenségi index legmagasabb értékei (30 vagy több) a magasabb elmozdulási energiájú csoportban nem gyakrabban találhatók meg, mint az alacsonyabb elmozdulási energiájú csoportban.

H 1 : Az elégtelenségi index legmagasabb értékei (30 vagy több) a nagyobb elmozdulási energiájú csoportban gyakoribbak, mint az alacsonyabb elmozdulási energiájú csoportban. Készítsünk egy négymezős táblázatot a táblázat adataiból. 5.4.

5.6. táblázat

Négycellás táblázat a φ*-kritérium kiszámításához a nagyobb és alacsonyabb elmozdulási energiájú csoportok összehasonlításakor a hiányossági index szintje szerint

Csoportok	A „Van hatás”* hiányjelzője nagyobb vagy egyenlő, mint 30		"Nincs hatás": A hiánypontszám alacsonyabb 30		Összegek
1. csoport - nagyobb elmozdulási energiával		(61,1%)		(38.9%)
2. csoport - alacsonyabb elmozdulási energiával		(25.0%)		(75.0%)
Összegek

táblázat szerint.XIIIAz 1. függelék megállapítja, hogy ez az eredmény p=0,008 szignifikanciaszintnek felel meg.

Válasz: De elutasítják. elfogadotthj: A legmagasabb hibaarány (30 vagy több pont) a csoportbanVal velnagyobb elmozdulási energiájú csoportban gyakoribbak, mint az alacsonyabb elmozdulási energiájú csoportban (p=0,008).

Így ezt be tudtuk bizonyítaniVcsoportVal velaz erőteljesebb elmozdulást az elégtelenségi mutató szélső értékei dominálják, és az a tény, hogy ez a mutató nagyobb az értékénélelérebben a konkrét csoportban.

Most megpróbálhatnánk bebizonyítani, hogy a nagyobb elmozdulási energiájú csoportban az elégtelenségi index alacsonyabb értékei is gyakoribbak, annak ellenére, hogy az átlagos értékV ez a csoport több (26,11 versus 15,42 a csoportbanVal vel kisebb elmozdulás).

Fogalmazzuk meg a hipotéziseket.

H 0 : A legalacsonyabb alultápláltsági pontszám (nulla) a csoportbanVal vel nagyobb elmozdulási energiát nem találunk gyakrabban, mint a csoportbanVal vel alacsonyabb elmozdulási energia.

H 1 : A legalacsonyabb alultápláltsági arány (nulla) fordul előV nagyobb elmozdulási energiájú csoport gyakrabban, mint a csoportbanVal vel kevésbé energikus elmozdulás. Csoportosítsuk az adatokat egy új négycellás táblába.

5.7. táblázat

Négycellás táblázat a különböző elmozdulási energiájú csoportok összehasonlításához a hiányossági index nulla értékeinek gyakorisága alapján

Csoportok	"Van hatás": az elégtelenség mutatója 0		"Nincs hatás" hiba	a kitevő nem 0	Összegek
1. csoport - nagyobb elmozdulási energiával		(27,8%)		(72,2%)
1 csoport - alacsonyabb elmozdulási energiával		(8,3%)		(91,7%)
Összegek

Meghatározzuk a φ értékeit és kiszámítjuk a φ* értékét:

Válasz: H 0 elutasítva. A legalacsonyabb hiánypontszámok (nulla) a magasabb elmozdulási energiájú csoportban gyakoribbak, mint az alacsonyabb elmozdulási energiájú csoportban (p<0,05).

Összegezve, a kapott eredmények bizonyítéknak tekinthetők Z. Freud és A. Adler komplex fogalmai részleges egybeesésére.

Lényeges, hogy az elmozdulási energia mutatója és a saját elégtelenség érzésének intenzitásának mutatója között a teljes mintában pozitív lineáris korrelációt kaptunk (p = +0,491, p<0,01). Как мы можем убедиться, применение критерия φ* позволяет проникнуть в более тонкие и содержательно значимые соотношения между этими двумя показателями.

4. példa - a φ* kritérium használata a kritériummal kombinálva λ Kolmogorov-Smirnov a maximum elérése érdekében pontoseredmény

Ha a mintákat néhány mennyiségileg mért mutató szerint hasonlítjuk össze, akkor felmerül a probléma annak az eloszlási pontnak a meghatározása, amely kritikusnak tekinthető, amikor az összes alanyt „hatással” és „nincs hatással” lévőkre osztjuk.

Elvileg elég tetszőlegesen megválasztható az a pont, ahol alcsoportokra osztanánk a csoportot, ahol van hatás és nincs hatás. Bármilyen hatás érdekelhet bennünket, ezért mindkét mintát bármikor két részre oszthatjuk, ha van valami értelme.

A φ* teszt teljesítményének maximalizálása érdekében azonban ki kell választani azt a pontot, ahol a legnagyobb a különbség a két összehasonlított csoport között. Ezt legpontosabban a kritériumszámítási algoritmus segítségével tehetjük megλ , amely lehetővé teszi a maximális eltérés pontjának megtalálását a két minta között.

A φ* és a kritériumok kombinálásának lehetőségeλ leírta E.V. Gubler (1978, 85-88. o.). Próbáljuk meg ezt a módszert használni a következő probléma megoldására.

Egy közös tanulmányban M.A. Kurochkina, E.V. Sidorenko és Yu.A. Churakov (1992) az Egyesült Királyságban az angol háziorvosokat két kategóriában kérdezték meg: a) orvosok, akik támogatták az orvosi reformot, és rendelőiket már saját költségvetésükből finanszírozó szervezetté alakították; b) orvosok, akiknek a fogadása továbbra sem rendelkezik saját forrással, és teljes egészében az állami költségvetésből biztosítják. A kérdőíveket 200 orvosból álló mintának küldték ki, akik az angol orvosok általános populációját reprezentálták a különböző nemű, életkorú, szolgálati idők és munkavégzés helye szerinti személyek – nagyvárosokban vagy tartományokban – reprezentációja tekintetében.

A kérdőívre 78 orvos küldött választ, közülük 50-en pénztáros, 28-an pénztári fogadáson dolgoznak. Mindegyik orvosnak meg kellett jósolnia, hogy a következő évben, 1993-ban mekkora lesz a pénzes fogadások aránya. A választ küldött 78 orvosból csak 70 válaszolt erre a kérdésre. Előrejelzéseik megoszlását a táblázat mutatja be. 5.8 külön egy pénztáros orvosi csoportra és egy pénztár nélküli orvoscsoportra.

Különböznek a pénzes és a pénz nélküli orvosok előrejelzései?

5.8. táblázat

A háziorvosok előrejelzéseinek megoszlása ​​a felvételi alapból való részesedésére vonatkozóan 1993-ban

Tervezett részesedés
fogadószobák pénzeszközökkel	pénztárral rendelkező orvosok (n 1 =45)	orvosok pénz nélkül (n 2 =25)	Összegek
1. 0-20%	4	5	9
2. 21-40%	15	ÉS	26
3. 41-60%	18	5	23
4. 61-80%	7	4	ÉS
5. 81-100%	1	0	1
Összegek	45	25	70

Határozzuk meg a maximális eltérés pontját a válaszok két eloszlása ​​között a 4.3. bekezdés 15. algoritmusa szerint (lásd 5.9. táblázat).

5.9. táblázat

A felhalmozott gyakoriságok maximális eltérésének kiszámítása két csoport orvosának előrejelzései eloszlásában

A pénzeszközökkel rendelkező nevelőszülők aránya (%)	Empirikus gyakoriságok adott válaszkategória kiválasztásához		Empirikus frekvenciák		Kumulatív empirikus gyakoriságok		Különbség (d)
	alapozó orvosok(n 1 =45)	orvosok pénz nélkül (n 2 =25)	f* uh 1	f* a2	∑f* e1	∑f* a1
1. 0-20% 2. 21-40% 3. 41-60% 4. 61-80% 5. 81-100%	4 15 18 7 1	5 11 5 4 0	0,089 0,333 0,400 0,156 0,022	0,200 0,440 0,200 0,160 0	0,089 0,422 0,822 0,978 1,000	0,200 0,640 0,840 1,000 1,000	0111 0,218 0,018 0,022 0

A két kumulált empirikus frekvencia között talált maximális különbség az0,218.

Ez a különbség az előrejelzés második kategóriájában halmozódik fel. Próbáljuk meg ennek a kategóriának a felső határát használni kritériumként ahhoz, hogy mindkét mintát egy alcsoportra ossza fel, ahol van hatás, és egy olyan alcsoportra, ahol nincs hatás. Feltételezzük, hogy van "hatása", ha ez az orvos a fogadószobák 41-100%-át jósolja meg pénzeszközökkel.1993 évben, és nincs hatása, ha egy adott orvos a műtétek 0-40%-át jósolja meg1993 év. Kombináljuk egyrészt az 1. és 2. előrejelzési kategóriát, másrészt a 3., 4. és 5. előrejelzési kategóriát. Az előrejelzések eredő megoszlását a táblázat mutatja be. 5.10.

5.10. táblázat

Előrejelzések terjesztése pénztáros és pénzeszköz nélküli orvosok számára

Az alappal rendelkező nevelőotthonok tervezett aránya (%1	Empirikus gyakoriságok adott előrejelzési kategória kiválasztásához		Összegek
	alapozó orvosok(n 1 =45)	pénztár nélkül orvosok(n 2 =25)
1. 0-40%	19	16	35
2. 41-től 100%-ig	26	9	35
Összegek	45	25	70

Az eredményül kapott táblázatot (5.10. táblázat) használhatjuk különböző hipotézisek tesztelésével, bármely két cellájának összehasonlításával. Emlékszünk rá, hogy ez az úgynevezett négycellás, vagy négymezős táblázat.

Ebben az esetben arra vagyunk kíváncsiak, hogy a már pénzzel rendelkező orvosok valóban nagyobb mozgást jósolnak-e a jövőben, mint a pénzzel nem rendelkező orvosok. Ezért feltételesen úgy gondoljuk, hogy van "hatás", ha az előrejelzés a 41-től 100%-ig terjedő kategóriába esik. A számítások egyszerűsítése érdekében most el kell forgatnunk a táblázatot 90°-kal, az óramutató járásával megegyező irányba forgatva. Akár szó szerint is megteheti, ha a könyvet az asztallal együtt forgatja. Most rátérhetünk a φ* kritérium kiszámítására szolgáló munkalapra - Fisher-féle szögtranszformáció.

asztal 5.11

Négycellás táblázat a Fisher-féle φ*-teszt kiszámításához a háziorvosok két csoportjának előrejelzései közötti különbségek azonosításához

Csoport	Van hatás - előrejelzés 41-100%	Nincs hatás – előrejelzés 0 és 40% között	Teljes
éncsoport - orvosok, akik vették az alapot	26 (57.8%)	19 (42.2%)	45
IIcsoport - orvosok, akik nem vették fel az alapot	9 (36.0%)	16 (64.0%)	25
Teljes	35	35	70

Fogalmazzuk meg a hipotéziseket.

H 0 : Személyek százalékos arányaaz összes orvosi fogadás 41%-100%-ára előrevetítve a pénzeszközök megoszlását, a pénzes orvosok csoportjában nincs több, mint a pénztelen orvosok körében.

H 1 : Az összes fogadás 41%-100%-ában a pénzelosztást előrejelzők aránya a pénztáros orvosok körében nagyobb, mint a pénzteleneknél.

Meghatározzuk a φ értékeit 1 és φ 2 táblázat szerintXIIFüggelék 1. Emlékezzünk rá, hogy φ 1 mindig a nagyobb százaléknak megfelelő szög.

Most határozzuk meg a φ* kritérium tapasztalati értékét:

táblázat szerint.XIIIAz 1. függelék meghatározza, hogy ez az érték milyen szignifikanciaszintnek felel meg: p=0,039.

Az 1. függelékben található ugyanezen táblázat szerint a φ* kritérium kritikus értékei határozhatók meg:

Válasz: De elutasítva (p=0,039). Azon emberek százalékos aránya, akik előre megjósolják a pénzeszközök elosztását41-100 % A pénztárat igénybe vevő orvosok csoportjában az összes recepciósnál meghaladja ezt az arányt a pénztárat nem igénybe vevő orvosok körében.

Vagyis a rendelőikben már külön költségvetésből dolgozó orvosok azt jósolják, hogy idén ez a gyakorlat jobban elterjed, mint azok az orvosok, akik még nem vállalták a külön költségvetésre való átállást. Ennek az eredménynek az értelmezése sokrétű. Feltételezhető például, hogy az egyes csoportok orvosai tudat alatt jellemzőbbnek tartják viselkedésüket. Ez azt is jelentheti, hogy azok az orvosok, akik már áttértek az önfenntartó költségvetésre, hajlamosak eltúlozni ennek a mozgalomnak a körét, hiszen döntésüket meg kell indokolniuk. A feltárt különbségek olyasmit is jelenthetnek, ami teljesen kívül esik a tanulmányban feltett kérdések keretein. Például, hogy az önálló költségvetésből dolgozó orvosok tevékenysége hozzájárul ahhoz, hogy a két csoport álláspontja közötti különbségek élesedjenek. Nagyon aktívak voltak, amikor beleegyeztek az alapok átvételébe, nagyon aktívak voltak, amikor vették a fáradságot, hogy válaszoljanak a levélben kiküldött kérdőívekre; aktívabbak, ha azt jósolják, hogy más orvosok aktívabbak lesznek a pénzeszközök fogadásában.

Így vagy úgy, de biztosak lehetünk abban, hogy a talált statisztikai eltérések mértéke ezeknél a valós adatoknál a lehető legnagyobb. A kritérium segítségével megállapítottukλ a két eloszlás közötti maximális eltérés pontja, és ezen a ponton osztották két részre a mintákat.

A jeled.