Lineáris egyenletrendszer megoldása a Cramer módszerrel. Egyenletrendszer megoldása Cramer, Gauss és inverz mátrix módszerekkel

A Cramer-módszer vagy az úgynevezett Cramer-szabály egyenletrendszerekből ismeretlen mennyiségek keresésének módszere. Csak akkor használható, ha a keresett értékek száma megegyezik a számmal algebrai egyenletek a rendszerben, vagyis a rendszerből kialakított főmátrixnak négyzet alakúnak kell lennie, és nem tartalmazhat nulla sort, és akkor is, ha a determinánsa nem lehet nulla.

1. tétel

Cramer tétele Ha az egyenletek együtthatói alapján összeállított főmátrix $D$ fődeterminánsa nem egyenlő nullával, akkor az egyenletrendszer konzisztens, és egyedi megoldása van. Egy ilyen rendszer megoldását a rendszerek megoldására szolgáló úgynevezett Cramer-képletek számítják ki lineáris egyenletek: $x_i = \frac(D_i)(D)$

Mi az a Cramer módszer?

Cramer módszerének lényege a következő:

1. Ahhoz, hogy a Cramer-módszerrel megoldást találjunk a rendszerre, először is kiszámítjuk a $D$ mátrix fő determinánsát. Ha a főmátrix számított determinánsa a Cramer-módszerrel számolva nullával egyenlő, akkor a rendszernek nincs egyetlen megoldása, vagy végtelen számú megoldása van. Ebben az esetben a rendszer általános vagy valamilyen alapvető válaszának megtalálásához a Gauss-módszer használata javasolt.
2. Ezután ki kell cserélni a legkülső oszlopot fő mátrix a szabad kifejezések oszlopába, és számítsa ki a $D_1$ determinánst.
3. Ismételje meg ugyanezt az összes oszlopra, és megkapja a determinánsokat $D_1$ és $D_n$ között, ahol $n$ a jobb szélső oszlop száma.
4. Az összes $D_1$...$D_n$ determináns megtalálása után az ismeretlen változók kiszámíthatók a $x_i = \frac(D_i)(D)$ képlettel.

A mátrix determinánsának kiszámítási technikái

A 2 x 2-nél nagyobb dimenziójú mátrix determinánsának kiszámításához többféle módszert használhat:

• A háromszögek szabálya, vagy Sarrus szabálya, amely ugyanerre a szabályra emlékeztet. A háromszög módszer lényege, hogy a determináns kiszámításakor az ábrán a jobb oldali piros vonallal összekötött összes szám szorzatát pluszjellel írjuk, a bal oldali ábrán pedig az összes hasonló módon összekötött szám szorzatát. mínuszjellel vannak írva. Mindkét szabály 3 x 3 méretű mátrixokra alkalmas. A Sarrus-szabály esetén először magát a mátrixot írjuk át, majd mellette annak első és második oszlopát is újraírjuk. A mátrixon átlókat húzunk, és a főátlón fekvő vagy azzal párhuzamosan fekvő további mátrixtagokat pluszjellel, a másodlagos átlón fekvő vagy azzal párhuzamos elemeket pedig mínuszjellel írjuk.

1. ábra: Háromszögszabály a Cramer-módszer determinánsának kiszámításához

• A Gauss-módszerként ismert módszert használva ezt a módszert néha a determináns sorrendjének csökkentésének is nevezik. Ebben az esetben a mátrixot átalakítják és háromszög alakúra redukálják, majd a főátlón lévő összes számot megszorozzák. Emlékeztetni kell arra, hogy ha ilyen módon keresünk egy determinánst, akkor nem lehet sorokat vagy oszlopokat számokkal szorozni vagy osztani anélkül, hogy kivennénk őket szorzóként vagy osztóként. Determináns keresése esetén csak akkor lehetséges a sorok és oszlopok egymáshoz való kivonása és összeadása, ha előzőleg a kivont sort egy nullától eltérő tényezővel megszoroztuk. Továbbá, amikor átrendezi a mátrix sorait vagy oszlopait, ne feledje, hogy meg kell változtatnia a mátrix végső jelét.
• Ha Cramer-módszerrel old meg egy 4 ismeretlent tartalmazó SLAE-t, akkor a legjobb a Gauss-módszer használata a determinánsok kereséséhez és megtalálásához, vagy a determináns meghatározásához kiskorúak keresésével.

Egyenletrendszerek megoldása Cramer módszerével

Alkalmazzuk Cramer módszerét 2 egyenletből és két szükséges mennyiségből álló rendszerre:

$\begin(esetek) a_1x_1 + a_2x_2 = b_1 \\ a_3x_1 + a_4x_2 = b_2 \\ \end(esetek)$

A kényelem kedvéért jelenítsük meg kiterjesztett formában:

$A = \begin(array)(cc|c) a_1 & a_2 & b_1 \\ a_3 & a_4 & b_1 \\ \end(array)$

Keressük meg a főmátrix determinánsát, amit a rendszer fődeterminánsának is neveznek:

$D = \begin(array)(|cc|) a_1 & a_2 \\ a_3 & a_4 \\ \end(array) = a_1 \cdot a_4 – a_3 \cdot a_2$

Ha a fődetermináns nem egyenlő nullával, akkor a slough Cramer-módszerrel történő megoldásához két további determinánst kell kiszámítani két mátrixból úgy, hogy a fő mátrix oszlopait szabad tagok sorával helyettesítjük:

$D_1 = \begin(array)(|cc|) b_1 & a_2 \\ b_2 & a_4 \\ \end(array) = b_1 \cdot a_4 – b_2 \cdot a_4$

$D_2 = \begin(array)(|cc|) a_1 & b_1 \\ a_3 & b_2 \\ \end(array) = a_1 \cdot b_2 – a_3 \cdot b_1$

Most keressük meg a $x_1$ és $x_2$ ismeretleneket:

$x_1 = \frac (D_1)(D)$

$x_2 = \frac (D_2)(D)$

1. példa

Cramer módszere SLAE-ek megoldására 3. rendű (3 x 3) főmátrixszal és három ismeretlennel.

Oldja meg az egyenletrendszert:

$\begin(esetek) 3x_1 – 2x_2 + 4x_3 = 21 \\ 3x_1 +4x_2 + 2x_3 = 9\\ 2x_1 – x_2 - x_3 = 10 \\ \end(esetek)$

Számítsuk ki a mátrix fődeterminánsát a fent, az 1. pont alatt leírt szabály segítségével:

$D = \begin(tömb)(|ccc|) 3 & -2 & 4 \\3 & 4 & -2 \\ 2 & -1 & 1 \\ \end(tömb) = 3 \cdot 4 \cdot ( -1) + 2 \cdot (-2) \cdot 2 + 4 \cdot 3 \cdot (-1) – 4 \cdot 4 \cdot 2 – 3 \cdot (-2) \cdot (-1) - (- 1) \cdot 2 \cdot 3 = - 12 - 8 -12 -32 - 6 + 6 = - 64 $

És most három másik meghatározó tényező:

$D_1 = \begin(array)(|cccc|) 21 & 2 & 4 \\ 9 & 4 & 2 \\ 10 & 1 & 1 \\ \end(array) = 21 \cdot 4 \cdot 1 + (- 2) \cdot 2 \cdot 10 + 9 \cdot (-1) \cdot 4 – 4 \cdot 4 \cdot 10 – 9 \cdot (-2) \cdot (-1) - (-1) \cdot 2 \ cdot 21 = - 84 - 40 - 36 - 160 - 18 + 42 = - 296 USD

$D_2 = \begin(array)(|cccc|) 3 & 21 & 4 \\3 & 9 & 2 \\ 2 & 10 & 1 \\ \end(array) = 3 \cdot 9 \cdot (- 1) + 3 \cdot 10 \cdot 4 + 21 \cdot 2 \cdot 2 – 4 \cdot 9 \cdot 2 – 21 \cdot 3 \cdot (-1) – 2 \cdot 10 \cdot 3 = - 27 + 120 + 84 – 72 + 63 – 60 = 108 dollár

$D_3 = \begin(array)(|cccc|) 3 & -2 & 21 \\ 3 & 4 & 9 \\ 2 & 1 & 10 \\ \end(array) = 3 \cdot 4 \cdot 10 + 3 \cdot (-1) \cdot 21 + (-2) \cdot 9 \cdot 2 – 21 \cdot 4 \cdot 2 - (-2) \cdot 3 \cdot 10 - (-1) \cdot 9 \cdot 3 = 120 – 63 – 36 – 168 + 60 + 27 = - 60 USD

Keressük meg a szükséges mennyiségeket:

$x_1 = \frac(D_1) (D) = \frac(-296)(-64) = 4 \frac(5)(8)$

$x_2 = \frac(D_1) (D) = \frac(108) (-64) = -1 \frac (11) (16)$

$x_3 = \frac(D_1) (D) = \frac(-60) (-64) = \frac (15) (16)$

Az első részben megnéztük néhány elméleti anyagot, a helyettesítési módszert, valamint a rendszeregyenletek tagonkénti összeadásának módszerét. Mindenkinek ajánlom, aki ezen az oldalon keresztül jutott el az oldalra, hogy olvassa el az első részt. Talán néhány látogató túl egyszerűnek találja az anyagot, de a lineáris egyenletrendszerek megoldása során számos nagyon fontos megjegyzést és következtetést tettem a megoldással kapcsolatban. matematikai problémákatáltalában.

És most elemezzük Cramer szabályát, valamint egy lineáris egyenletrendszer megoldását a segítségével inverz mátrix(mátrix módszer). Az összes anyagot egyszerűen, részletesen és áttekinthetően mutatjuk be, szinte minden olvasó képes lesz megtanulni a rendszerek megoldását a fenti módszerekkel.

Először is közelebbről megvizsgáljuk a Cramer-szabályt két ismeretlenben lévő két lineáris egyenletrendszerre. Minek? - Végül is a legegyszerűbb rendszer iskolamódszerrel, a tanévenkénti összeadás módszerével oldható meg!

A helyzet az, hogy bár néha, de előfordul egy ilyen feladat - két ismeretlennel rendelkező lineáris egyenletrendszer megoldása Cramer képleteivel. Másodszor, egy egyszerűbb példa segít megérteni, hogyan kell használni a Cramer-szabályt egy bonyolultabb esetre – egy három egyenletrendszerre három ismeretlennel.

Ezen kívül vannak két változós lineáris egyenletrendszerek, amelyeket Cramer-szabály segítségével célszerű megoldani!

Tekintsük az egyenletrendszert

Első lépésben kiszámítjuk a determinánst, ezt ún a rendszer fő meghatározója.

Gauss módszer.

Ha , akkor a rendszernek egyedi megoldása van, és a gyökök megtalálásához további két determinánst kell kiszámítanunk:
És

A gyakorlatban a fenti minősítők is jelölhetők latin betű.

Az egyenlet gyökereit a következő képletekkel keressük meg:
,

7. példa

Oldjon meg egy lineáris egyenletrendszert!

Megoldás: Látjuk, hogy az egyenlet együtthatói elég nagyok, a jobb oldalon ott vannak tizedesjegyek vesszővel. A vessző meglehetősen ritka vendég gyakorlati feladatokat a matematikában ezt a rendszert egy ökonometriai feladatból vettem át.

Hogyan lehet megoldani egy ilyen rendszert? Megpróbálhatja az egyik változót egy másikkal kifejezni, de ebben az esetben valószínűleg szörnyű díszes törteket kap, amelyekkel rendkívül kényelmetlen a munka, és a megoldás kialakítása egyszerűen borzasztóan fog kinézni. A második egyenletet megszorozhatja 6-tal, és tagonként kivonhatja, de itt is ugyanazok a törtek keletkeznek.

Mit tegyek? Ilyen esetekben a Cramer-féle képletek segítenek.

;

;

Válasz: ,

Mindkét gyökér végtelen végű, és megközelítőleg megtalálható, ami meglehetősen elfogadható (sőt közhely) ökonometriai problémák esetén.

Itt nincs szükség megjegyzésekre, mivel a feladatot kész képletekkel oldják meg, azonban van egy figyelmeztetés. Ennek a módszernek a használatakor kötelező A feladatterv egy töredéke a következő részlet: „Ez azt jelenti, hogy a rendszernek egyedi megoldása van”. Ellenkező esetben a bíráló megbüntethet Cramer tételének figyelmen kívül hagyása miatt.

Nem lenne felesleges ellenőrizni, ami kényelmesen elvégezhető egy számológépen: a közelítő értékeket behelyettesítjük a rendszer minden egyenlete bal oldalába. Ennek eredményeként egy kis hibával olyan számokat kell kapnia, amelyek a jobb oldalon vannak.

8. példa

Adja meg a választ közönséges helytelen törtekkel! Csinálj egy ellenőrzést.

Ez egy példa, amelyet önállóan kell megoldania (példa a végső tervre és a válaszra a lecke végén).

Térjünk át a Cramer-szabályra egy három egyenletrendszerre, három ismeretlennel:

Megtaláljuk a rendszer fő meghatározóját:

Ha , akkor a rendszernek végtelen sok megoldása van, vagy inkonzisztens (nincs megoldása). Ebben az esetben a Cramer-szabály nem segít, a Gauss-módszert kell használni.

Ha , akkor a rendszernek egyedi megoldása van, és a gyökök megtalálásához további három determinánst kell kiszámítanunk:
, ,

És végül a választ a következő képletekkel számítjuk ki:

Amint láthatja, a „háromszor három” eset alapvetően nem különbözik a „kettő-kettő” esettől, a szabad kifejezések oszlopa egymás után balról jobbra „sétál” a fődetermináns oszlopai mentén.

9. példa

Oldja meg a rendszert Cramer-képletekkel!

Megoldás: Oldjuk meg a rendszert Cramer képleteivel.

, ami azt jelenti, hogy a rendszer egyedi megoldással rendelkezik.

Válasz: .

Igazából itt sincs semmi különösebb kommentár, ami abból adódik, hogy a megoldás kész képleteket követ. De van egy-két megjegyzés.

Előfordul, hogy a számítások eredményeként „rossz” irreducibilis törteket kapunk, például: .
A következő „kezelési” algoritmust ajánlom. Ha nincs kéznél számítógép, tegye a következőket:

1) Hiba lehet a számításokban. Amint „rossz” törttel találkozik, azonnal ellenőriznie kell Helyesen van átírva a feltétel?. Ha a feltételt hibák nélkül írják át, akkor a determinánsokat újra kell számolni egy másik sor (oszlop) bővítésével.

2) Ha az ellenőrzés eredményeként nem találunk hibát, akkor valószínűleg elírás történt a feladat feltételeiben. Ilyenkor nyugodtan és ÓVATOSAN dolgozd végig a feladatot a végéig, majd feltétlenül ellenőrizzeés a döntés után tiszta lapra felvonjuk. Természetesen a töredékes válasz ellenőrzése kellemetlen feladat, de lefegyverző érv lesz a tanár számára, aki nagyon szeret mínuszt adni minden olyan marhaságért, mint a . A törtek kezelésének módját a 8. példa válasza írja le részletesen.

Ha van kéznél számítógép, akkor az ellenőrzéshez használjon egy automata programot, amely a lecke elején ingyenesen letölthető. Egyébként a legjövedelmezőbb a program azonnali használata (még a megoldás elindítása előtt azonnal megjelenik a közbenső lépés, ahol hibázott); Ugyanez a számológép automatikusan kiszámítja a megoldást a rendszer számára mátrix módszer.

Második megjegyzés. Időről időre vannak olyan rendszerek, amelyek egyenletéből hiányzik néhány változó, például:

Itt az első egyenletben nincs változó, a másodikban nincs változó. Ilyen esetekben nagyon fontos, hogy helyesen és Óvatosan írjuk le a fő meghatározót:
– a hiányzó változók helyére nullák kerülnek.
Egyébként ésszerű a determinánsokat nullákkal nyitni aszerint, hogy melyik sorban (oszlopban) van a nulla, mivel észrevehetően kevesebb a számítás.

10. példa

Oldja meg a rendszert Cramer-képletekkel!

Ez egy példa egy független megoldásra (minta a végső tervből és a válasz a lecke végén).

Egy 4 egyenletből és 4 ismeretlennel rendelkező rendszer esetében a Cramer-képleteket hasonló elvek szerint írják fel. Élő példát láthat a Determinánsok tulajdonságai című leckében. A determináns sorrendjének csökkentése - öt 4. rendű determináns eléggé megoldható. Bár a feladat már nagyon emlékeztet egy professzor cipőjére egy szerencsés diák mellkasán.

A rendszer megoldása inverz mátrix segítségével

Az inverz mátrix módszer lényegében egy speciális eset mátrix egyenlet(Lásd a megadott lecke 3. példáját).

A szakasz tanulmányozásához képesnek kell lennie a determinánsok kiterjesztésére, a mátrix inverzének megkeresésére és a mátrixszorzás végrehajtására. A magyarázatok előrehaladtával a releváns linkeket megadjuk.

11. példa

Oldja meg a rendszert mátrix módszerrel!

Megoldás: Írjuk fel a rendszert mátrix formában:
, Hol

Kérjük, nézze meg az egyenlet- és mátrixrendszert. Szerintem mindenki érti azt az elvet, amivel elemeket írunk mátrixokba. Az egyetlen megjegyzés: ha néhány változó hiányzik az egyenletekből, akkor a mátrix megfelelő helyeire nullákat kell tenni.

Az inverz mátrixot a következő képlettel találjuk meg:
, ahol a mátrix megfelelő elemeinek algebrai komplementereinek transzponált mátrixa.

Először is nézzük a meghatározót:

Itt a determináns az első sorban bővül.

Figyelem! Ha , akkor az inverz mátrix nem létezik, és a rendszer mátrix módszerrel megoldhatatlan. Ebben az esetben a rendszert az ismeretlenek kiküszöbölésének módszere (Gauss-módszer) oldja meg.

Most ki kell számítanunk 9 kiskorút, és be kell írnunk a minors mátrixba

Referencia: Hasznos tudni a kettős alsó indexek jelentését a lineáris algebrában. Az első számjegy annak a sornak a száma, amelyben az elem található. A második számjegy annak az oszlopnak a száma, amelyben az elem található:

Azaz a dupla alsó index azt jelzi, hogy az elem az első sorban, a harmadik oszlopban van, és például az elem a 3 sorban, 2 oszlopban van.

Legyen a lineáris egyenletrendszer annyi egyenletet, ahány független változó, azaz. úgy néz ki

Az ilyen lineáris egyenletrendszereket másodfokúnak nevezzük. A determinánst, amely a rendszer független változóinak együtthatóiból áll (1.5), a rendszer fő determinánsának nevezzük. Jelölni fogjuk görög levél D. Szóval

. (1.6)

Ha a fődetermináns egy tetszőleges ( j th) oszlopot, cserélje ki a rendszer szabad feltételeinek oszlopára (1.5), akkor megkaphatja n kiegészítő minősítők:

(j = 1, 2, …, n). (1.7)

Cramer szabálya másodfokú lineáris egyenletrendszerek megoldása a következő. Ha az (1.5) rendszer D fődeterminánsa eltér nullától, akkor a rendszernek van egy egyedi megoldása, amely a következő képletekkel kereshető:

(1.8)

1.5. példa. Oldja meg az egyenletrendszert Cramer módszerével!

.

Számítsuk ki a rendszer fő meghatározóját:

D¹0 óta a rendszernek van egy egyedi megoldása, amelyet az (1.8) képletekkel találhatunk meg:

Így,

Műveletek mátrixokon

1. Egy mátrix szorzása egy számmal. A mátrix számmal való szorzásának műveletét a következőképpen definiáljuk.

2. Ahhoz, hogy egy mátrixot megszorozzon egy számmal, minden elemét meg kell szorozni ezzel a számmal. Azaz

. (1.9)

Példa 1.6. .

Mátrix összeadás.

Ezt a műveletet csak azonos sorrendű mátrixokra vezetjük be.

Két mátrix hozzáadásához hozzá kell adni egy másik mátrix megfelelő elemeit egy mátrix elemeihez:

(1.10)
A mátrixösszeadás műveletének az asszociativitási és kommutativitási tulajdonságai vannak.

Példa 1.7. .

Mátrixszorzás.

Ha a mátrixoszlopok száma A egybeesik a mátrix sorok számával IN, akkor az ilyen mátrixokhoz bevezetjük a szorzási műveletet:

2

Így egy mátrix szorzásakor A méretek m´ n a mátrixhoz IN méretek n´ k mátrixot kapunk VEL méretek m´ k. Ebben az esetben a mátrixelemek VEL a következő képletekkel számítják ki:

Probléma 1.8. Ha lehetséges, keresse meg a mátrixok szorzatát ABÉs B.A.:

Megoldás. 1) Azért, hogy munkát találjak AB, mátrixsorokra van szüksége A szorozzuk meg mátrixoszlopokkal B:

2) Munka B.A. nem létezik, mert a mátrixoszlopok száma B nem egyezik a mátrix sorok számával A.

Inverz mátrix. Lineáris egyenletrendszerek megoldása mátrix módszerrel

Mátrix A- 1-et négyzetmátrix inverzének nevezzük A, ha az egyenlőség teljesül:

hol keresztül én a mátrixszal azonos sorrendű identitásmátrixot jelöli A:

.

Ahhoz, hogy egy négyzetmátrixnak legyen inverze, szükséges és elégséges, hogy a determinánsa nullától eltérő legyen. Az inverz mátrixot a következő képlet segítségével találjuk meg:

, (1.13)

Ahol A ij- algebrai kiegészítések elemekhez a ij mátrixok A(Megjegyzendő, hogy algebrai összeadások mátrixsorokhoz A az inverz mátrixban találhatók megfelelő oszlopok formájában).

Példa 1.9. Keresse meg az inverz mátrixot A- 1 a mátrixhoz

.

Az inverz mátrixot az (1.13) képlet segítségével találjuk meg, amely az esetre n= 3 alakja:

.

Keressünk det A = | A| = 1 × 3 × 8 + 2 × 5 × 3 + 2 × 4 × 3 - 3 × 3 × 3 - 1 × 5 × 4 - 2 × 2 × 8 = 24 + 30 + 24 - 27 - 20 - 32 = - 1. Mivel az eredeti mátrix determinánsa nem nulla, létezik az inverz mátrix.

1) Keress algebrai komplementereket! A ij:

Az inverz mátrix megtalálásának kényelme érdekében az eredeti mátrix soraihoz az algebrai összeadásokat a megfelelő oszlopokba helyeztük.

A kapott algebrai összeadásokból új mátrixot állítunk össze, és elosztjuk a det determinánssal A. Így kapjuk az inverz mátrixot:

A nem nulla fődeterminánsú lineáris egyenletrendszerek másodfokú egyenletrendszerei megoldhatók az inverz mátrix segítségével. Ehhez az (1.5) rendszert mátrix formában írjuk fel:

Ahol

A bal oldali egyenlőség mindkét oldalát (1,14) megszorozva ezzel A- 1, megkapjuk a rendszer megoldását:

, hol

Így egy négyzetes rendszer megoldásához meg kell találni a rendszer főmátrixának inverz mátrixát, és meg kell szorozni a jobb oldalon a szabad tagok oszlopmátrixával.

1.10. probléma. Oldjon meg egy lineáris egyenletrendszert!

az inverz mátrix segítségével.

Megoldás.Írjuk fel a rendszert mátrix formában: ,

Ahol - a rendszer főmátrixa, - az ismeretlenek oszlopa és - a szabad kifejezések oszlopa. Mivel a rendszer fő meghatározója , akkor a rendszer fő mátrixa A inverz mátrixa van A-1. Megtalálni az inverz mátrixot A-1 , kiszámítjuk a mátrix összes elemére az algebrai komplementereket A:

A kapott számokból mátrixot állítunk össze (és a mátrix soraihoz algebrai összeadásokat Aírja be a megfelelő oszlopokba), és ossza el a D determinánssal. Így megkaptuk az inverz mátrixot:

A rendszer megoldását az (1.15) képlet segítségével találjuk meg:

Így,

Lineáris egyenletrendszerek megoldása a szokásos Jordan eliminációs módszerrel

Legyen egy tetszőleges (nem feltétlenül másodfokú) lineáris egyenletrendszer:

(1.16)

Megoldást kell találni a rendszerre, pl. olyan változóhalmaz, amely kielégíti az (1.16) rendszer összes egyenlőségét. IN általános eset rendszernek (1.16) nem csak egy megoldása lehet, hanem számtalan megoldása is lehet. Az is lehet, hogy egyáltalán nincsenek megoldásai.

Az ilyen problémák megoldása során a jól ismert iskolai tanfolyami módszert alkalmazzák az ismeretlenek kiküszöbölésére, amelyet a szokásos Jordan eliminációs módszernek is neveznek. Ennek a módszernek az a lényege, hogy az (1.16) rendszer egyik egyenletében az egyik változót más változókkal fejezzük ki. Ezt a változót ezután a rendszer más egyenleteibe helyettesítik. Az eredmény egy olyan rendszer, amely egy egyenlettel és egy változóval kevesebb, mint az eredeti rendszer. Emlékszik az egyenletre, amelyből a változót kifejezték.

Ezt a folyamatot addig ismételjük, amíg egy utolsó egyenlet nem marad a rendszerben. Az ismeretlenek kiküszöbölésének folyamata révén egyes egyenletek valódi azonossággá válhatnak, pl. Az ilyen egyenletek ki vannak zárva a rendszerből, mivel a változók bármely értékére teljesülnek, és ezért nem befolyásolják a rendszer megoldását. Ha az ismeretlenek kiküszöbölése során legalább egy egyenlet olyan egyenlőséggé válik, amely nem teljesülhet a változók egyetlen értékére sem (például), akkor arra a következtetésre jutunk, hogy a rendszernek nincs megoldása.

Ha a megoldás során nem merülnek fel ellentmondó egyenletek, akkor a benne maradt változók egyikét az utolsó egyenletből találjuk meg. Ha csak egy változó maradt az utolsó egyenletben, akkor azt számként fejezzük ki. Ha más változók az utolsó egyenletben maradnak, akkor azokat paramétereknek tekintjük, és a rajtuk keresztül kifejezett változó ezeknek a paramétereknek a függvénye lesz. Ezután megtörténik az úgynevezett „fordított mozgás”. A talált változót behelyettesíti az utoljára emlékezett egyenletbe, és megtalálja a második változót. Ezután a két talált változót behelyettesítjük az utolsó előtti memorizált egyenletbe, és megtaláljuk a harmadik változót, és így tovább, egészen az első memorizált egyenletig.

Ennek eredményeként megoldást kapunk a rendszerre. Ez a megoldás akkor lesz egyedi, ha a talált változók számok. Ha az első talált változó, majd az összes többi a paraméterektől függ, akkor a rendszernek végtelen számú megoldása lesz (minden paraméterkészlet egy új megoldásnak felel meg). Azokat a képleteket, amelyek lehetővé teszik, hogy egy adott paraméterkészlettől függően megoldást találjon egy rendszerre, a rendszer általános megoldásának nevezzük.

Példa 1.11.

x

Az első egyenlet memorizálása után és hasonló kifejezéseket hozva a második és harmadik egyenletbe, a rendszerhez jutunk:

Kifejezzük y a második egyenletből, és cserélje be az első egyenletbe:

Emlékezzünk a második egyenletre, és az elsőből megtaláljuk z:

Visszafelé dolgozva következetesen azt találjuk yÉs z. Ehhez először behelyettesítjük az utoljára emlékezett egyenletbe, ahonnan megtaláljuk y:

.

Ezután behelyettesítjük az első memorizált egyenletbe hol találhatjuk meg x:

1.12. probléma. Oldjon meg egy lineáris egyenletrendszert az ismeretlenek kiiktatásával:

. (1.17)

Megoldás. Fejezzük ki az első egyenletből származó változót xés cseréld be a második és harmadik egyenletbe:

.

Emlékezzünk az első egyenletre

Ebben a rendszerben az első és a második egyenlet ellentmond egymásnak. Valóban, kifejezve y , azt kapjuk, hogy 14 = 17. Ez az egyenlőség nem áll fenn a változók egyik értékére sem x, y, És z. Ebből következően az (1.17) rendszer inkonzisztens, i.e. nincs megoldása.

Arra kérjük az olvasókat, hogy saját maguk ellenőrizzék, hogy az eredeti rendszer fő meghatározója (1.17) egyenlő-e nullával.

Tekintsünk egy olyan rendszert, amely csak egy szabad taggal különbözik az (1.17) rendszertől.

1.13. probléma. Oldjon meg egy lineáris egyenletrendszert az ismeretlenek kiiktatásával:

. (1.18)

Megoldás. Mint korábban, az első egyenletből származó változót fejezzük ki xés cseréld be a második és harmadik egyenletbe:

.

Emlékezzünk az első egyenletre és mutasson be hasonló kifejezéseket a második és harmadik egyenletben. Megérkezünk a rendszerhez:

Kifejezése y az első egyenletből, és behelyettesítjük a második egyenletbe , a 14 = 14 azonosságot kapjuk, ami nem befolyásolja a rendszer megoldását, ezért kizárható a rendszerből.

Az utolsó emlékezett egyenlőségben a változó z paraméternek fogjuk tekinteni. hiszünk. Majd

Cseréljük yÉs z az első emlékezett egyenlőségbe és megtalálni x:

.

Így az (1.18) rendszernek végtelen számú megoldása van, és bármilyen megoldás megtalálható az (1.19) képletekkel, a paraméter tetszőleges értékével t:

(1.19)
Tehát a rendszer megoldásai például a következő változóhalmazok (1; 2; 0), (2; 26; 14) stb. Az (1.19) képletek az (1.18) rendszer általános (bármely) megoldását fejezik ki ).

Abban az esetben, ha az eredeti rendszer (1.16) elegendő nagy számban egyenletek és ismeretlenek, a szokásos Jordan elimináció jelzett módszere nehézkesnek tűnik. Ez azonban nem igaz. Elegendő egy algoritmust levezetni a rendszeregyütthatók egy lépésben történő újraszámítására általános nézetés speciális Jordan-táblázatok formájában fogalmazza meg a probléma megoldását.

Legyen adott egy lineáris alakzat (egyenlet) rendszer:

, (1.20)
Ahol x j- független (keresett) változók, a ij- állandó esélyek
(i = 1, 2,…, m; j = 1, 2,…, n). A rendszer jobb részei y i (i = 1, 2,…, m) lehetnek változók (függők) vagy állandók. Erre a rendszerre megoldást kell találni az ismeretlenek kiiktatásával.

Tekintsük a következő műveletet, amelyet ezentúl „a szokásos Jordan-kiesések egy lépésének” neveznek. tetszőleges ( r th) egyenlőség tetszőleges változót ( xs) és helyettesíti az összes többi egyenlőséggel. Ez persze csak akkor lehetséges, ha egy rs¹ 0. Együttható egy rs feloldó (néha irányító vagy fő) elemnek nevezzük.

A következő rendszert kapjuk:

. (1.21)

Tól s- rendszeregyenlőség (1.21), ezt követően megtaláljuk a változót xs(miután a többi változót megtaláltuk). S A -edik sort megjegyzi, és ezt követően kizárja a rendszerből. A fennmaradó rendszer egy egyenletet és egy kevésbé független változót fog tartalmazni, mint az eredeti rendszer.

Számítsuk ki a kapott rendszer (1.21) együtthatóit az eredeti rendszer (1.20) együtthatóin keresztül. Kezdjük azzal r egyenlet, amely a változó kifejezése után xs a többi változón keresztül így fog kinézni:

Így az új együtthatók r az egyenleteket a következő képletekkel számítjuk ki:

(1.23)
Most számoljuk ki az új együtthatókat b ij(én¹ r) tetszőleges egyenlet. Ehhez helyettesítsük be az (1.22)-ben kifejezett változót. xs V én rendszer egyenlete (1.20):

Hasonló kifejezések megadása után a következőket kapjuk:

(1.24)
Az (1.24) egyenlőségből olyan képleteket kapunk, amelyekkel kiszámítjuk az (1.21) rendszer fennmaradó együtthatóit (kivéve r egyenlet):

(1.25)
A lineáris egyenletrendszerek transzformációját a szokásos Jordan elimináció módszerével táblázatok (mátrixok) formájában mutatjuk be. Ezeket a táblázatokat „jordániai tábláknak” nevezik.

Így az (1.20) probléma a következő Jordan-táblázathoz kapcsolódik:

1.1. táblázat

	x 1	x 2	…	x j	…	xs	…	x n
y 1 =	a 11	a 12		a 1j		a 1s		a 1n
…………………………………………………………………..
y i=	a i 1	a i 2		a ij		a is		a be
…………………………………………………………………..
y r=	a r 1	a r 2		egy rj		egy rs		arn
………………………………………………………………….
y n=	a m 1	a m 2		egy mj		a ms		a mn

A Jordan 1.1-es tábla egy bal oldali fejlécoszlopot tartalmaz, amelybe a rendszer jobb oldali részei (1.20), és egy felső fejlécsort tartalmaznak, amelybe a független változókat írják.

A táblázat többi eleme alkotja az (1.20) rendszer együtthatóinak fő mátrixát. Ha megszorozod a mátrixot A a felső címsor elemeiből álló mátrixhoz kapunk egy mátrixot, amely a bal oldali címoszlop elemeiből áll. Azaz lényegében a Jordan-tábla egy lineáris egyenletrendszer felírásának mátrixa: . Az (1.21) rendszer a következő Jordan-táblázatnak felel meg:

1.2. táblázat

	x 1	x 2	…	x j	…	y r	…	x n
y 1 =	b 11	b 12		b 1 j		b 1 s		b 1 n
…………………………………………………………………..
y i =	b i 1	b i 2		b ij		b az		b in
…………………………………………………………………..
x s =	b r 1	b r 2		b rj		b rs		brn
………………………………………………………………….
y n =	b m 1	b m 2		b mj		bms		b mn

Megengedő elem egy rs Ezeket félkövérrel emeljük ki. Emlékezzünk vissza, hogy a Jordan elimináció egy lépésének végrehajtásához a feloldó elemnek nullától eltérőnek kell lennie. Az engedélyező elemet tartalmazó táblázatsort engedélyező sornak nevezzük. Az engedélyezési elemet tartalmazó oszlopot engedélyezés oszlopnak nevezzük. Amikor egy adott tábláról a következő táblára lépünk, egy változó ( xs) a táblázat felső fejlécsorából a bal oldali fejlécoszlopba kerül, és fordítva, a rendszer egyik szabad tagja ( y r) a táblázat bal oldali fejoszlopából a felső fejsorba lép.

Ismertesse az együtthatók újraszámításának algoritmusát, amikor az (1.1) Jordan táblából az (1.2) táblába lépünk, ami az (1.23) és (1.25) képletekből következik.

1. A feloldó elemet az inverz szám helyettesíti:

2. A feloldó karakterlánc többi elemét felosztjuk a feloldó elemre, és az előjelet az ellenkezőjére változtatjuk:

3. A felbontás oszlop többi elemét a felbontási elemre osztjuk:

4. Az engedélyező sorban és oszlopban nem szereplő elemek újraszámítása a következő képletekkel történik:

Az utolsó képlet könnyen megjegyezhető, ha észreveszi, hogy az elemek, amelyek a tört , a kereszteződésben vannak én-ja és r sorok és jés s oszlopok (feloldó sor, feloldó oszlop, valamint az a sor és oszlop, amelynek metszéspontjában az újraszámított elem található). Pontosabban a képlet memorizálásánál a következő diagramot használhatja:

-21 -26 -13 -37

A Jordan kivételek első lépésének végrehajtásakor az 1.3. táblázat oszlopaiban található bármely elemét kiválaszthatja feloldó elemként x 1 ,…, x 5 (az összes megadott elem nem nulla). Csak ne az utolsó oszlopban jelölje ki az engedélyező elemet, mert független változókat kell találnia x 1 ,…, x 5. Például kiválasztjuk az együtthatót 1 változóval x 3 az 1.3. táblázat harmadik sorában (az engedélyező elem félkövéren van szedve). Az 1.4 táblázatra lépve a változó x A felső fejlécsor 3-a felcserélődik a bal oldali fejlécoszlop (harmadik sor) konstans 0-jával. Ebben az esetben a változó x 3 a fennmaradó változókon keresztül fejeződik ki.

Húr x 3 (1.4. táblázat) előzetes emlékezés után kizárható az 1.4. táblázatból. Az 1.4. táblázatból kimarad a harmadik oszlop, ahol a felső címsor nulla található. A lényeg az, hogy az esélyektől függetlenül ennek az oszlopnak b i 3 az egyes 0 egyenletek összes megfelelő tagját b i 3 rendszer nulla lesz. Ezért ezeket az együtthatókat nem kell kiszámítani. Egy változó kiküszöbölése x 3 és az egyik egyenletre emlékezve az 1.4 táblázatnak megfelelő rendszerhez jutunk (a vonal áthúzva x 3). Az 1.4 táblázatban feloldó elemként kijelölés b 14 = -5, ugorjon az 1.5 táblázathoz. Az 1.5. táblázatban emlékezzen az első sorra, és zárja ki a táblázatból a negyedik oszloppal együtt (nulla a tetején).

1.5. táblázat 1.6

Az utolsó 1.7 táblázatból a következőket találjuk: x 1 = - 3 + 2x 5 .

A már megtalált változókat következetesen behelyettesítve a megjegyzett sorokba, megtaláljuk a fennmaradó változókat:

Így a rendszernek végtelen sok megoldása van. Változó x 5, tetszőleges értékek rendelhetők hozzá. Ez a változó paraméterként működik x 5 = t. Bebizonyítottuk a rendszer kompatibilitását és megtaláltuk általános megoldás:

x 1 = - 3 + 2t

x 2 = - 1 - 3t

x 3 = - 2 + 4t . (1.27)
x 4 = 4 + 5t

x 5 = t

Paraméter megadása t különböző jelentések, végtelen számú megoldást kapunk az eredeti rendszerre. Így például a rendszer megoldása a következő változóhalmaz (- 3; - 1; - 2; 4; 0).

Cramer módszere a determinánsok felhasználásán alapul lineáris egyenletrendszerek megoldásában. Ez jelentősen felgyorsítja a megoldás folyamatát.

A Cramer-módszerrel annyi lineáris egyenletből álló rendszert lehet megoldani, ahány egyenletben ismeretlen van. Ha a rendszer determinánsa nem egyenlő nullával, akkor Cramer módszere használható a megoldásban, de ha egyenlő nullával, akkor nem. Ezenkívül a Cramer-módszer használható olyan lineáris egyenletrendszerek megoldására is, amelyek egyedi megoldással rendelkeznek.

Meghatározás. Az ismeretlenek együtthatóiból álló determinánst a rendszer determinánsának nevezzük, és delta-nak nevezzük.

Meghatározók

úgy kapjuk meg, hogy a megfelelő ismeretlenek együtthatóit szabad kifejezésekkel helyettesítjük:

;

.

Cramer tétele. Ha a rendszer determinánsa nem nulla, akkor a lineáris egyenletrendszernek egyetlen megoldása van, és az ismeretlen egyenlő a determinánsok arányával. A nevező a rendszer determinánsát tartalmazza, a számláló pedig azt a determinánst, amelyet a rendszer determinánsából kapunk úgy, hogy ennek az ismeretlennek az együtthatóit szabad tagokkal helyettesítjük. Ez a tétel tetszőleges sorrendű lineáris egyenletrendszerre érvényes.

1. példa Oldjon meg egy lineáris egyenletrendszert:

Szerint Cramer tétele nálunk van:

Tehát a (2) rendszer megoldása:

online számológép, Cramer megoldási módszere.

Három eset lineáris egyenletrendszerek megoldásánál

Amint az abból kiderül Cramer tétele, lineáris egyenletrendszer megoldása során három eset fordulhat elő:

Első eset: a lineáris egyenletrendszernek egyedi megoldása van

(a rendszer következetes és határozott)

Második eset: egy lineáris egyenletrendszernek végtelen számú megoldása van

(a rendszer konzisztens és bizonytalan)

** ,

azok. az ismeretlenek és a szabad tagok együtthatói arányosak.

Harmadik eset: a lineáris egyenletrendszernek nincs megoldása

(inkonzisztens a rendszer)

Tehát a rendszer m lineáris egyenletek -val n változóknak nevezzük nem ízületi, ha nincs egyetlen megoldása, és közös, ha van legalább egy megoldása. Egy szimultán egyenletrendszert, amelynek csak egy megoldása van, nevezzük bizonyosés több mint egy bizonytalan.

Példák lineáris egyenletrendszerek megoldására Cramer módszerrel

Adott legyen a rendszer

.

Cramer tétele alapján

………….
,

Ahol
-

rendszer meghatározó. A fennmaradó determinánsokat úgy kapjuk meg, hogy az oszlopot a megfelelő változó (ismeretlen) együtthatóira cseréljük szabad tagokkal:

2. példa

.

Ezért a rendszer határozott. A megoldás megtalálásához kiszámítjuk a determinánsokat

A Cramer-képleteket használva a következőket kapjuk:

Tehát (1; 0; -1) az egyetlen megoldás a rendszerre.

A 3 x 3 és 4 x 4 egyenletrendszerek megoldásainak ellenőrzéséhez használhat egy online számológépet a Cramer megoldási módszerével.

Ha egy lineáris egyenletrendszerben egy vagy több egyenletben nincsenek változók, akkor a determinánsban a megfelelő elemek nullával egyenlők! Ez a következő példa.

3. példa Oldjon meg egy lineáris egyenletrendszert a Cramer módszerrel:

.

Megoldás. Megtaláljuk a rendszer meghatározóját:

Nézze meg figyelmesen az egyenletrendszert és a rendszer determinánsát, és ismételje meg a választ arra a kérdésre, hogy mely esetekben egyenlő a determináns egy vagy több eleme nullával! Tehát a determináns nem egyenlő nullával, ezért a rendszer határozott. A megoldás megtalálásához kiszámítjuk az ismeretlenek determinánsait

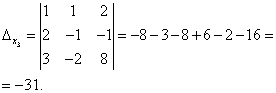
A Cramer-képleteket használva a következőket kapjuk:

Tehát a rendszer megoldása: (2; -1; 1).

A 3 x 3 és 4 x 4 egyenletrendszerek megoldásainak ellenőrzéséhez használhat egy online számológépet a Cramer megoldási módszerével.

Az oldal tetejére

Továbbra is közösen oldjuk meg a rendszereket Cramer módszerével

Mint már említettük, ha a rendszer determinánsa egyenlő nullával, és az ismeretlenek determinánsai nem egyenlőek nullával, akkor a rendszer inkonzisztens, vagyis nincs megoldása. Illusztráljuk a következő példával.

6. példa. Oldjon meg egy lineáris egyenletrendszert a Cramer módszerrel:

Megoldás. Megtaláljuk a rendszer meghatározóját:

A rendszer determinánsa nulla, ezért a lineáris egyenletrendszer vagy inkonzisztens és határozott, vagy inkonzisztens, vagyis nincs megoldása. Az egyértelműség kedvéért kiszámítjuk az ismeretlenek determinánsait

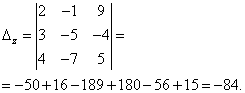
Az ismeretlenek determinánsai nem egyenlőek nullával, ezért a rendszer inkonzisztens, vagyis nincs megoldása.

A 3 x 3 és 4 x 4 egyenletrendszerek megoldásainak ellenőrzéséhez használhat egy online számológépet a Cramer megoldási módszerével.

A lineáris egyenletrendszereket érintő feladatokban vannak olyanok is, ahol a változókat jelölő betűk mellett más betűk is vannak. Ezek a betűk egy számot jelölnek, leggyakrabban valódit. A gyakorlatban az ilyen egyenletekhez és egyenletrendszerekhez bármely jelenség vagy objektum általános tulajdonságainak keresésének problémái vezetnek. Vagyis feltaláltál valamit új anyag vagy egy eszközt, és annak leírásához, amelyek egy példány méretétől vagy számától függetlenül gyakoriak, egy lineáris egyenletrendszert kell megoldani, ahol a változók együtthatói helyett betűk vannak. Nem kell messzire keresni a példákat.

A következő példa egy hasonló problémára vonatkozik, csak az egyenletek, változók és egy bizonyos valós számot jelölő betűk száma növekszik.

8. példa. Oldjon meg egy lineáris egyenletrendszert a Cramer módszerrel:

Megoldás. Megtaláljuk a rendszer meghatározóját:

Determinánsok keresése ismeretlenekre

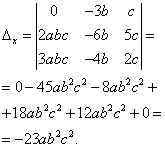
A Cramer módszert olyan lineáris algebrai egyenletrendszerek (SLAE) megoldására használják, amelyekben az ismeretlen változók száma megegyezik az egyenletek számával, és a fő mátrix determinánsa nem nulla. Ebben a cikkben megvizsgáljuk, hogyan találhatók meg az ismeretlen változók a Cramer-módszerrel, és hogyan kaphatunk képleteket. Ezek után térjünk át a példákra, és írjuk le részletesen a lineáris algebrai egyenletrendszerek megoldását Cramer módszerével.

Oldalnavigáció.

Cramer-módszer – képletek levezetése.

Alakú lineáris egyenletrendszert kell megoldanunk

Ahol x 1, x 2, …, x n ismeretlen változók, a i j, i = 1, 2, …, n, j = 1, 2, …, n- numerikus együtthatók, b 1, b 2, ..., b n - szabad tagok. Egy SLAE megoldása egy olyan x 1 , x 2 , …, x n értékhalmaz, amelyre a rendszer összes egyenlete azonossággá válik.

Mátrix formában ezt a rendszert úgy írhatjuk fel, hogy A ⋅ X = B, ahol - a rendszer fő mátrixa, elemei ismeretlen változók együtthatói, - a mátrix szabad kifejezések oszlopa, és - a mátrix ismeretlen változók oszlopa. Az x 1, x 2, …, x n ismeretlen változók megtalálása után a mátrix az egyenletrendszer megoldásává válik, és az A ⋅ X = B egyenlőség azonossággá.

Feltételezzük, hogy az A mátrix nem szinguláris, azaz a determinánsa nem nulla. Ebben az esetben a lineáris algebrai egyenletrendszernek van egy egyedi megoldása, amelyet Cramer módszerével találhatunk meg. (A rendszerek megoldásának módszereit a Lineáris algebrai egyenletek rendszerei című fejezet tárgyalja).

A Cramer-módszer a mátrixdetermináns két tulajdonságán alapul:

Tehát kezdjük el megkeresni az ismeretlen x 1 változót. Ehhez megszorozzuk a rendszer első egyenletének mindkét részét A 1 1-gyel, a második egyenlet mindkét részét A 2 1-gyel, és így tovább, az n-edik egyenlet mindkét részét A n 1-gyel (azaz mi szorozzuk meg a rendszer egyenleteit a mátrix első A oszlopának megfelelő algebrai komplementereivel):

Adjuk össze a rendszeregyenlet bal oldalát, csoportosítsuk az ismeretlen változókkal rendelkező x 1, x 2, ..., x n tagokat, és ezt az összeget egyenlővé tegyük az egyenletek összes jobb oldalának összegével:

Ha rátérünk a determináns korábban említett tulajdonságaira, akkor megvan

és az előző egyenlőség azt a formát ölti

ahol

Hasonlóképpen x 2-t találunk. Ehhez megszorozzuk a rendszeregyenletek mindkét oldalát az A mátrix második oszlopának algebrai komplementereivel:

Összeadjuk a rendszer összes egyenletét, csoportosítjuk az ismeretlen változók tagjait x 1, x 2, ..., x n, és alkalmazzuk a determináns tulajdonságait:

Ahol
.

A fennmaradó ismeretlen változókat hasonló módon találjuk meg.

Ha kijelöljük

Akkor kapunk képletek ismeretlen változók megtalálásához Cramer módszerével .

Megjegyzés.

Ha a lineáris algebrai egyenletrendszer homogén, az , akkor csak triviális megoldása van (at ). Valóban, nulla szabad kifejezés esetén minden meghatározó nullával egyenlőek lesznek, mivel nulla elemekből álló oszlopot fognak tartalmazni. Ezért a képletek fog adni.

Algoritmus lineáris algebrai egyenletrendszerek megoldására Cramer módszerrel.

Írjuk fel algoritmus lineáris algebrai egyenletrendszerek megoldására Cramer módszerrel.

Példák lineáris algebrai egyenletrendszerek megoldására Cramer módszerével.

Nézzünk meg néhány példa megoldását.

Példa.

Keressen megoldást egy inhomogén lineáris algebrai egyenletrendszerre Cramer módszerével .

Megoldás.

A rendszer fő mátrixának alakja . Számítsuk ki a determinánsát a képlet segítségével :

Mivel a rendszer főmátrixának determinánsa nem nulla, az SLAE egyedi megoldással rendelkezik, és ezt Cramer módszerével találhatjuk meg. Írjuk fel a determinánsokat és . A rendszer főmátrixának első oszlopát felcseréljük egy szabad tagok oszlopával, és megkapjuk a determinánst . Ehhez hasonlóan a főmátrix második oszlopát a szabad kifejezések oszlopára cseréljük, és megkapjuk.

Kiszámítjuk ezeket a determinánsokat:

Keresse meg az ismeretlen x 1 és x 2 változókat a képletekkel! :

Ellenőrizzük. Helyettesítsük be a kapott x 1 és x 2 értékeket az eredeti egyenletrendszerbe:

A rendszer mindkét egyenlete azonossággá alakul, így a megoldást helyesen találtuk meg.

Válasz:

.

Az SLAE fő mátrixának egyes elemei egyenlőek lehetnek nullával. Ebben az esetben a megfelelő ismeretlen változók hiányoznak a rendszeregyenletekből. Nézzünk egy példát.

Példa.

Keressen megoldást egy lineáris egyenletrendszerre Cramer módszerével .

Megoldás.

Írjuk át a rendszert a formába , így láthatóvá válik a rendszer fő mátrixa . Keressük meg a determinánsát a képlet segítségével

megvan

A fő mátrix determinánsa nem nulla, ezért a lineáris egyenletrendszernek egyedi megoldása van. Keressük meg Cramer módszerével. Számítsuk ki a determinánsokat :

Így,

Válasz:

Az ismeretlen változók megnevezése a rendszeregyenletekben eltérhet x 1, x 2, ..., x n-től. Ez nem befolyásolja a döntési folyamatot. De a rendszer egyenleteiben az ismeretlen változók sorrendje nagyon fontos a fő mátrix és a Cramer-módszer szükséges determinánsainak összeállításakor. Tisztázzuk ezt a pontot egy példával.

Példa.

Cramer módszerével keress megoldást egy három lineáris algebrai egyenletrendszerre három ismeretlenben .

Megoldás.

Ebben a példában az ismeretlen változók jelölése eltérő (x, y és z x1, x2 és x3 helyett). Ez nem befolyásolja a megoldást, de legyen óvatos a változó jelölésekkel. NEM veheted a rendszer fő mátrixának . A rendszer összes egyenletében először rendezni kell az ismeretlen változókat. Ehhez átírjuk az egyenletrendszert így . Most már jól látható a rendszer fő mátrixa . Számítsuk ki a determinánsát:

A fő mátrix determinánsa nem nulla, ezért az egyenletrendszernek egyedi megoldása van. Keressük meg Cramer módszerével. Írjuk fel a meghatározókat (ügyeljen a jelölésre), és számítsa ki őket:

Továbbra is meg kell keresni az ismeretlen változókat a képletekkel :

Ellenőrizzük. Ehhez szorozza meg a fő mátrixot a kapott megoldással (ha szükséges, lásd a részt):

Ennek eredményeként az eredeti egyenletrendszer szabad tagjainak oszlopát kaptuk, így a megoldást helyesen találtuk meg.

Válasz:

x = 0, y = -2, z = 3.

Példa.

Oldjon meg egy lineáris egyenletrendszert Cramer módszerével! , ahol a és b néhány valós szám.

Megoldás.

Válasz:

Példa.

Keresse meg az egyenletrendszer megoldását! Cramer módszerével - valamilyen valós szám.

Megoldás.

Számítsuk ki a rendszer főmátrixának determinánsát: . kifejezés egy intervallum, ezért bármilyen valós értékre. Következésképpen az egyenletrendszernek van egy egyedi megoldása, amelyet Cramer módszerével találhatunk meg. Kiszámoljuk és: