Negyedrendű definíció. Mátrix meghatározó
A felsőbb matematikai feladatok megoldása során nagyon gyakran felmerül az igény számítsuk ki egy mátrix determinánsát. A mátrix determinánsa megjelenik a lineáris algebrában, analitikus geometria, matematikai elemzés és egyéb szakaszok felsőbb matematika. Így egyszerűen lehetetlen nélkülözni a determinánsok megoldásának készségét. Önellenőrzéshez ingyenesen letölthet egy determináns-kalkulátort, amely önmagában nem tanítja meg a determinánsok megoldását, de nagyon kényelmes, hiszen mindig előnyös, ha előre tudja a helyes választ!
Nem fogok szigorú matematikai meghatározást adni a determinánsnak, és általában megpróbálom minimalizálni a matematikai terminológiát, ez nem fogja megkönnyíteni a legtöbb olvasó dolgát. Ennek a cikknek az a célja, hogy megtanítsa Önnek a másod-, harmad- és negyedrendű determinánsok megoldását. Az összes anyagot egyszerű és hozzáférhető formában mutatják be, és még egy teljes (üres) teáskanna is a magasabb matematikában, az anyag alapos tanulmányozása után, képes lesz helyesen megoldani a meghatározó tényezőket.
A gyakorlatban leggyakrabban találhatunk másodrendű determinánst, például: és harmadrendű determinánst, például: 
.
Negyedrendű determináns 
Szintén nem antik, és a lecke végén kitérünk rá.
Remélem mindenki érti a következőket: A determináns belsejében lévő számok önmagukban élnek, és szó sincs kivonásról! A számokat nem lehet felcserélni!
(Különösen lehetséges egy determináns sorainak vagy oszlopainak páronkénti átrendezése előjelének megváltoztatásával, de gyakran ez nem szükséges - lásd a következő leckét: A determináns tulajdonságai és a sorrend csökkentése)
Így ha bármilyen determináns adott, akkor Semmihez sem nyúlunk benne!
Megnevezések: Ha adott egy mátrix 
, akkor a determinánsát jelöljük. Nagyon gyakran a determinánst is jelölik latin betű vagy görögül.
1)Mit jelent egy meghatározót megoldani (megtalálni, felfedni)? A determináns kiszámítása a SZÁM MEGTALÁLÁSA. A fenti példákban a kérdőjelek teljesen hétköznapi számok.
2) Most még ki kell találni HOGYAN találhatom meg ezt a számot? Ehhez bizonyos szabályokat, képleteket és algoritmusokat kell alkalmaznia, amelyekről most lesz szó.
Kezdjük a "kettő" determinánssal a "kettő":
ERRE EMLÉKEZTETNI KELL, legalábbis az egyetemi felsőfokú matematika tanulmányai során.
Nézzünk rögtön egy példát:
Kész. A legfontosabb az, hogy NE VEGYED BE A JELZÉSEKET.
Háromszor három mátrix determinánsa 8 féleképpen nyitható, ebből 2 egyszerű és 6 normál.
Kezdjük kettővel egyszerű módokon
Hasonlóan a két-két determinánshoz, a háromszoros determináns is kibővíthető a következő képlettel:
A képlet hosszú, és gondatlanságból könnyen hibázhatunk. Hogyan kerüljük el a bosszantó hibákat? Erre a célra egy második módszert találtak ki a determináns kiszámítására, amely valójában egybeesik az elsővel. Sarrus-módszernek vagy „párhuzamos szalagok” módszernek hívják.
A lényeg az, hogy a determinánstól jobbra rendelje hozzá az első és a második oszlopot, és óvatosan rajzoljon vonalakat ceruzával:
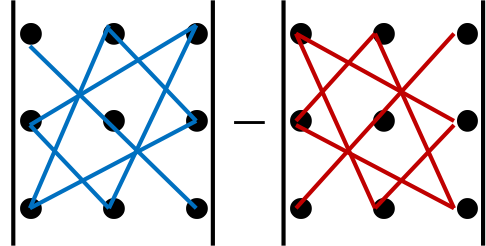
A „piros” átlókon található szorzók „plusz” jellel szerepelnek a képletben.
A „kék” átlókon található szorzók mínuszjellel szerepelnek a képletben:
Példa:
Hasonlítsa össze a két megoldást. Könnyen belátható, hogy ez UGYANOR, csak a második esetben a képlettényezők kissé átrendeződnek, és ami a legfontosabb, sokkal kisebb a tévedés valószínűsége.
Most nézzük meg a hat szokásos módszert a determináns kiszámítására
Miért normális? Mert az esetek túlnyomó többségében így kell nyilvánosságra hozni a minősítőket.
Ahogy észrevette, a háromszor három meghatározónak három oszlopa és három sora van.
A determinánst kinyitva oldhatod meg bármely sor vagy oszlop szerint.
Így 6 módszer létezik, minden esetben használva azonos típusú algoritmus.
A mátrix determinánsa megegyezik a sor (oszlop) elemeinek a megfelelő algebrai komplementerek szorzatának összegével. Ijedős? Minden sokkal egyszerűbb, nem tudományos, de érthető megközelítést alkalmazunk, amely még a matematikától távol álló ember számára is elérhető.
A következő példában kibővítjük a determinánst az első sorban.
Ehhez szükségünk van egy jelmátrixra: . Könnyen észrevehető, hogy a táblák sakktábla-mintázatban vannak elrendezve.
Figyelem! A jelmátrix saját találmányom. Ez a fogalom nem tudományos, nem kell használni a feladatok végső tervezésénél, csupán a determináns számítási algoritmusának megértésében segít.
Először a teljes megoldást adom. Ismét vesszük kísérleti determinánsunkat, és elvégezzük a számításokat:
És a fő kérdés: HOGYAN vehetjük ki ezt a „háromszor három” determinánsból: 
?
Tehát a „háromszor három” determináns három kis determináns megoldásához vezet le, vagy ahogyan más néven, MINOROV. Javaslom, hogy emlékezzen a kifejezésre, főleg, hogy emlékezetes: minor – kicsi.
Miután kiválasztottuk a determináns lebontásának módszerét az első sorban, nyilvánvaló, hogy minden körülötte forog:
Az elemek általában balról jobbra néznek (vagy fentről lefelé, ha egy oszlopot jelöltek ki)
Menjünk, először a sor első elemével, azaz eggyel foglalkozunk:
1) A jelek mátrixából kiírjuk a megfelelő jelet: 
2) Ezután felírjuk magát az elemet: 
3) MENTESEN húzza át azt a sort és oszlopot, amelyben az első elem megjelenik: 
A maradék négy szám alkotja a „kettő-kettő” determinánst, amelyet ún KIS egy adott elem (egység).
Térjünk át a sor második elemére.
4) A jelek mátrixából kiírjuk a megfelelő jelet:
5) Ezután írja be a második elemet: 
6) MENTESEN húzza át azt a sort és oszlopot, amelyben a második elem megjelenik: 
Nos, az első sor harmadik eleme. Nincs eredetiség:
7) A jelek mátrixából kiírjuk a megfelelő jelet: 
8) Írja le a harmadik elemet: 
9) MENTÁLISAN húzd át a harmadik elemet tartalmazó sort és oszlopot: 
A maradék négy számot kis determinánsba írjuk.
A fennmaradó akciók nem okoznak nehézséget, hiszen már tudjuk, hogyan kell számolni a két-két meghatározó tényezőt. NE VESZEDJEN MEG A JELZÉSEKBEN!
Hasonlóképpen, a determináns bármely sorra vagy oszlopra kiterjeszthető. Természetesen mind a hat esetben ugyanaz a válasz.
A négyszer-négy determináns kiszámítható ugyanazzal az algoritmussal.
Ebben az esetben a jelmátrixunk növekedni fog:
A következő példában kibővítettem a determinánst a negyedik oszlop szerint:
Hogyan történt, próbáld meg kitalálni magad. További információk később jönnek. Ha valaki a végére akarja megoldani a determinánst, a helyes válasz: 18. Gyakorlás céljából jobb, ha a determinánst valamilyen más oszlop vagy sor segítségével oldja meg.
Gyakorolni, feltárni, számolni nagyon jó és hasznos. De mennyi időt fog tölteni a nagy selejtezővel? Nincs gyorsabb és megbízhatóbb módszer? Azt javaslom, hogy ismerkedjen meg hatékony módszerek determinánsok számítása a második leckében - A determináns tulajdonságai. A determináns sorrendjének csökkentése.
VIGYÁZAT!
A második sorrend a főátlót alkotó számok szorzata és a másodlagos átlón lévő számok szorzata közötti különbség, a determinánsra a következő jelölés található: ; ; ; detA(döntő).
.
Példa: 
.
Harmadrendű mátrix determinánsa a következő szabály szerint kiszámított szám vagy matematikai kifejezés
A harmadrendű determináns kiszámításának legegyszerűbb módja, ha összeadjuk a determináns alatti első két sort.
A kapott számtáblázatban a főátlón és a fővel párhuzamos átlókon elhelyezkedő elemek szorozódnak, a szorzat eredményének előjele nem változik. A számítások következő szakasza az oldalátlón található és a vele párhuzamos elemek hasonló szorzása. A termékeredmények jelei fordítottak. Ezután összeadjuk a kapott hat tagot.
Példa:
Egy determináns bontása egy bizonyos sor (oszlop) elemeire.
Kisebb M ij elem és ij négyzetmátrix A mátrixelemekből álló determináns A, a törlés után megmaradt én- oh vonalak és j oszlop.
Például a kisebb elemhez a 21 harmadrendű mátrixok 
lesz meghatározó 
.
Azt fogjuk mondani, hogy az elem és ij páros helyet foglal el, ha i+j(melyek metszéspontjában lévő sor- és oszlopszámok összege: ezt az elemet) - páros szám, páratlan hely, ha i+j- páratlan szám.
Algebrai komplementer A ij elem és ij négyzetmátrix A kifejezésnek nevezzük 
(vagy a megfelelő minor értéke, a „+” jellel, ha a mátrixelem páros, a „-” jellel, ha az elem páratlan helyet foglal el).
Példa: 
a 23= 4;
- egy elem algebrai komplementere a 22= 1.
Laplace-tétel. A determináns egyenlő egy bizonyos sor (oszlop) elemeinek és a hozzájuk tartozó algebrai komplementerek szorzatának összegével.
Szemléltessük egy harmadrendű determináns példájával. A harmadrendű determinánst úgy számíthatja ki, hogy az első sort a következőképpen bővíti:
Hasonlóképpen kiszámíthatja a harmadrendű determinánst, ha bármelyik sort vagy oszlopot kibontja. Célszerű a determinánst a több nullát tartalmazó sor (vagy oszlop) mentén kiterjeszteni.
Példa: 
Így a 3. rendű determináns számítása 3 másodrendű determináns számítására redukálódik. IN általános eset kiszámolhatja egy négyzetmátrix determinánsát n-edik sorrend, a számításra redukálva n meghatározó tényezők ( n-1)-edik sorrend
Megjegyzés. Nincsenek egyszerű módszerek a determinánsok pontosabb kiszámítására magasrendű, hasonlóan a 2. és 3. rendű determinánsok számítási módszereihez. Ezért a harmadik rend feletti determinánsok kiszámításához csak a kiterjesztési módszer használható.
Példa. Számítsa ki a negyedrendű determinánst!
Bővítsük ki a determinánst a harmadik sor elemeire
A determinánsok tulajdonságai:
1. A determináns nem változik, ha sorait oszlopokkal helyettesítjük, és fordítva.
2. Két szomszédos sor (oszlop) átrendezésekor a determináns előjelet vált az ellenkezőjére.
3. Egy két azonos sorral (oszloppal) rendelkező determináns 0-val egyenlő.
4. A determináns egy bizonyos sorának (oszlopának) összes elemének közös tényezője kivehető a determináns előjeléből.
5. A determináns nem változik, ha bármely másik oszlop (sor) megfelelő elemeit hozzáadjuk valamelyik oszlopának (sorának) elemeihez, megszorozva egy bizonyos számmal.
Legyen egy n x n méretű A négyzetmátrix.
Meghatározás. A determináns az elemek összes lehetséges szorzatának algebrai összege, amelyet az A mátrix minden oszlopából és sorából veszünk. Ha minden ilyen szorzatban (a determináns tagjában) a tényezők az oszlopok sorrendjében vannak elrendezve (vagyis a szorzatban az a ij elemek második indexei növekvő sorrendben vannak), akkor a (+) előjellel azok olyan termékeket veszünk, amelyeknél az első indexek permutációja páros, és előjellel (-) – azokat, amelyeknél páratlan.
.
Itt van az inverziók száma az i 1, i 2, ..., i n indexek permutációjában.
Determinánsok megtalálásának módszerei
- Mátrix determinánsa sor- és oszlopbontással minorokon keresztül.
- Determináns háromszög alakúra redukálással (Gauss-módszer)
A determinánsok tulajdonságai
- Amikor egy mátrixot transzponálunk, a determinánsa nem változik.
- Ha egy determináns két sorát vagy két oszlopát felcseréli, a determináns előjelét változtatja, de abszolút értékében nem.
- Legyen C = AB ahol A és B négyzetmátrixok. Ekkor detC = detA ∙ detB.
- A két azonos sorral vagy két azonos oszloppal rendelkező determináns egyenlő 0-val. Ha egy bizonyos sor vagy oszlop minden eleme nulla, akkor maga a determináns nulla.
- A két arányos sorból vagy oszlopból álló determináns 0.
- A háromszög alakú mátrix determinánsa megegyezik az átlós elemek szorzatával. Az átlós mátrix determinánsa megegyezik a főátlón lévő elemek szorzatával.
- Ha egy sor (oszlop) minden elemét ugyanazzal a számmal szorozzuk meg, akkor a determináns ezzel a számmal lesz szorozva.
- Ha egy determináns egy bizonyos sorának (oszlopának) minden elemét két tag összegeként adjuk meg, akkor a determináns egyenlő két determináns összegével, amelyekben ezen egy kivételével minden sor (oszlop) azonos, és ez a sor (oszlop) az első determináns az első, a másodikban pedig a második kifejezés.
- Jacobi tétele: Ha a determináns egy bizonyos oszlopának elemeihez hozzáadjuk egy másik oszlop megfelelő elemeit, megszorozva egy tetszőleges λ tényezővel, akkor a determináns értéke nem változik.
- transzponált mátrix;
- bármely karakterlánchoz adjon hozzá egy másik karakterláncot tetszőleges számmal megszorozva.
1. feladat. Számítsa ki a determinánst soronkénti vagy oszloponkénti bővítéssel.
Megoldás :xml :xls
1. példa :xml :xls
2. feladat. Számítsa ki a determinánst kétféleképpen: a) a „háromszögek” szabály segítségével; b) vonal mentén történő bővítés.
Megoldás.
a) A mínusz előjelben szereplő kifejezések az oldalátlóhoz képest ugyanígy vannak megszerkesztve.
| = |
b) A mátrixot a következő formában írjuk fel:
| A= |
|
Fő meghatározó:
∆ = 2 (0 0-2 4)-(-1 (2 0-2 1))+(-2 (2 4-0 1)) = -34
3. feladat. Adja meg, hogy egy A negyedrendű négyzetmátrix determinánsa mekkora, ha rangja r(A)=1.
Válasz: det(A) = 0.
"Ha meg akarsz tanulni úszni, akkor bátran szállj a vízbe, és ha meg akarsz tanulni problémákat megoldani, Azt megoldani őket.»
D. Polya (1887-1985)
(Matematikus. Közreműködött nagy hozzájárulás a matematika népszerűsítésében.
Számos könyvet írt a problémák megoldásáról és a problémamegoldás tanításáról.) Minden négyzetmátrixhoz társítva szám . Ezt a számot hívják döntő mátrixok. A determináns kiszámítása speciális szabályok szerint történik, és |A|, det A
, ΔA. A determináns sorainak (oszlopainak) számát annak nevezzük.
sorrendben Elsőrendű meghatározó mátrix egyenlő az elemmel
a 11: |A|=a 11
Ne keverje össze az elsőrendű determinánst a modulussal. Másodrendű determináns
szimbólum jelzi és egyenlő
|A|=a 11 a 22 -a 12 a 21 3. rendű meghatározó
szimbólum jelzi A képlet emlékezéséhez használjon sematikus szabályokat ()
háromszög vagy Sarrus-szabály
Sarrus uralma.
Háromszög szabály.
Nézzünk egy példát ezeknek a szabályoknak a használatára.
PÉLDA:
Sarrus uralkodik
Adjuk hozzá az első két oszlopot a determinánshoz.
Háromszög szabály
Ez a determinánsszámítási módszer nem alkalmas 4-es és magasabb rendű determinánsokhoz. Mielőtt meghatározna egy olyan szabályt, amely lehetővé teszi bármilyen sorrendű determinánsok megtalálását, fontolja meg a mátrixelem algebrai komplementerének fogalmát. (A ij Algebrai komplementer és ij) elem A a mátrix meghatározója
Nézzünk egy példát ezeknek a szabályoknak a használatára.
egy szám, amely egyenlő a (-1) i+j szorzatával (a sorszám plusz ennek az elemnek az oszlopszámának hatványa) és a determinánssal, amelyet az adottból úgy kapunk, hogy áthúzzuk azt a sort és oszlopot, ahol ez elem található. Számítsa ki az algebrai komplementet elem a 21 .
A 21
Az algebrai komplement definíciója szerint
Tetszőleges sorrend determinánsának kiszámítása. A determináns egyenlő bármely sora (vagy oszlopa) elemeinek a megfelelő algebrai komplementerek szorzatának összegével.
, a 4. rendű determináns kiterjesztése az első sor mentén a következő:
