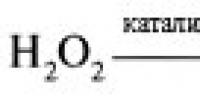Egész képlet. Az egész számok megértése

Mit jelent egy egész szám?

Tehát nézzük meg, milyen számokat nevezünk egész számoknak.

Így a következő számokat egész számokkal jelöljük: $0$, $±1$, $±2$, $±3$, $±4$ stb.

A természetes számok halmaza az egész számok halmazának részhalmaza, azaz. Bármely természetes szám egész szám lesz, de nem minden egész természetes szám.

Pozitív és negatív egész számok

2. definíció

plusz.

A $3, 78, 569, 10450$ számok pozitív egész számok.

3. definíció

előjeles egész számok mínusz.

A $−3, −78, −569, -10450$ számok negatív egész számok.

1. megjegyzés

A nulla szám sem nem pozitív, sem nem negatív egész szám.

Pozitív egész számok nullánál nagyobb egész számok.

Negatív egész számok nullánál kisebb egész számok.

A természetes egészek halmaza az összes pozitív egész halmaza, az összes ellentétes természetes szám halmaza pedig az összes negatív egész halmaza.

Nem pozitív és nem negatív egész számok

Minden pozitív egész számot és nullát hívunk nem negatív egész számok.

Nem pozitív egész számok mind negatív egész számok és a $0$ szám.

Jegyzet 2

És így, nem negatív egész szám nullánál nagyobb vagy nullával egyenlő egész számok, és nem pozitív egész szám– nullánál kisebb vagy nullával egyenlő egész számok.

Például nem pozitív egész számok: $−32, −123, 0, −5$ és nem negatív egész számok: $54, 123, 0, 856 342.$

Mennyiségváltozások leírása egész számokkal

Az egész számok az objektumok számában bekövetkezett változások leírására szolgálnak.

Nézzünk példákat.

1. példa

Hagyja, hogy egy bolt bizonyos számú terméket árusítson. Amikor a boltba 520 dollárnyi áru érkezik, az áruházban lévő cikkek száma növekedni fog, és az 520 dolláros szám pozitív irányú változást mutat a számban. Amikor az üzlet 50 dolláros árucikkeket ad el, az üzletben lévő termékek száma csökken, az 50 dollár pedig a szám változását fejezi ki negatív oldala. Ha az üzlet nem szállít és nem ad el árut, akkor az áruk darabszáma változatlan marad (azaz nulla számváltozásról beszélhetünk).

A fenti példában az áruk számának változását a $520$, $−50$ és $0$ egész számokkal írjuk le. Az $520$ egész szám pozitív értéke a szám pozitív irányú változását jelzi. A $−50$ egész szám negatív értéke a szám negatív irányú változását jelzi. A $0$ egész szám azt jelzi, hogy a szám megváltoztathatatlan.

Az egész számok használata kényelmes, mert... nincs szükség a szám növekedésének vagy csökkenésének kifejezett jelzésére - az egész szám előjele a változás irányát, az érték pedig a mennyiségi változást jelzi.

Egész számokkal nem csak mennyiségi változást, hanem tetszőleges mennyiség változását is kifejezhetjük.

Nézzünk egy példát egy termék költségének változására.

2. példa

Az érték növekedését, például 20 USD rubel értékkel, pozitív egész számmal fejezzük ki, 20 USD dollárral. Az árcsökkenés például $5$ rubel értékben egy negatív egész számmal írható le $−5$. Ha nincs értékváltozás, akkor ezt a változást a $0$ egész szám segítségével határozzuk meg.

Nézzük külön a negatív egész számok jelentését, mint az adósság összegét.

3. példa

Például egy személynek 5000 dollár rubelje van. Ezután az $5,000$ pozitív egész szám használatával megmutathatja, hány rubel van nála. Egy személynek 7000 USD rubel bérleti díjat kell fizetnie, de nincs ilyen pénze, ebben az esetben az ilyen helyzetet negatív egész szám írja le -7 000 USD. Ebben az esetben a személynek –7000 USD rubelje van, ahol a „–” az adósságot, a 7000 USD szám pedig az adósság összegét jelöli.

Ebben a cikkben meghatározzuk az egész számok halmazát, megvizsgáljuk, mely egész számokat nevezzük pozitívnak és melyeket negatívnak. Azt is bemutatjuk, hogyan használjuk az egész számokat bizonyos mennyiségek változásainak leírására. Kezdjük az egész számok meghatározásával és példáival.

Egész számok. Definíció, példák

Először is emlékezzünk a természetes számokról ℕ. Már maga a név is azt sugallja, hogy ezek olyan számok, amelyeket ősidők óta természetesen számlálásra használnak. Az egész számok fogalmának lefedéséhez ki kell terjesztenünk a természetes számok definícióját.

Definíció 1. Egész számok

Az egész számok a természetes számok, ellentéteik és a nulla szám.

Az egész számok halmazát a ℤ betű jelöli.

A természetes számok halmaza ℕ a ℤ egész számok részhalmaza. Minden természetes szám egész szám, de nem minden egész természetes szám.

A definícióból az következik, hogy az 1, 2, 3 számok bármelyike ​​egész szám. . , a 0 szám, valamint a - 1, - 2, - 3, . .

Ennek megfelelően példákat adunk. A 39, - 589, 10000000, - 1596, 0 számok egész számok.

Legyen a koordinátavonal vízszintesen megrajzolva és jobbra irányítva. Vessünk egy pillantást rá, hogy megjelenítsük az egész számok helyét egy vonalon.

A koordináta egyenes origója a 0 számnak felel meg, a nulla mindkét oldalán lévő pontok pedig pozitív és negatív egész számoknak felelnek meg. Minden pont egyetlen egész számnak felel meg.

Egy egész szám koordinátájú vonal bármely pontjához eljuthat, ha az origóból bizonyos számú egységszakaszt félreteszünk.

Pozitív és negatív egész számok

Az összes egész szám közül logikus a pozitív és a negatív egész számok megkülönböztetése. Adjuk meg a definícióikat.

2. definíció: Pozitív egész számok

A pozitív egész számok pluszjellel ellátott egész számok.

Például a 7-es szám egy egész szám pluszjellel, azaz pozitív egész szám. A koordinátavonalon ez a szám a referenciaponttól jobbra található, amelyet 0-nak kell tekinteni. További példák pozitív egész számokra: 12, 502, 42, 33, 100500.

3. definíció: Negatív egész számok

A negatív egész számok mínuszjellel rendelkező egész számok.

Példák negatív egész számokra: - 528, - 2568, - 1.

A 0 elválasztja a pozitív és negatív egész számokat, és maga sem nem pozitív, sem nem negatív.

Minden olyan szám, amely a pozitív egész szám ellentéte, definíció szerint negatív egész szám. Ennek az ellenkezője is igaz. Bármely negatív egész szám inverze pozitív egész szám.

A negatív és pozitív egész számok definícióinak más megfogalmazásai is megadhatók a nullával való összehasonlításukkal.

Definíció 4. Pozitív egész számok

A pozitív egész számok olyan egész számok, amelyek nagyobbak nullánál.

5. definíció: Negatív egész számok

A negatív egész számok olyan egész számok, amelyek nullánál kisebbek.

Ennek megfelelően a pozitív számok a koordináta egyenes origójától jobbra, a negatív egészek pedig a nullától balra.

Korábban azt mondtuk, hogy a természetes számok egész számok részhalmaza. Tisztázzuk ezt a pontot. A természetes számok halmaza pozitív egész számokból áll. A negatív egész számok halmaza viszont a természetesekkel ellentétes számok halmaza.

Fontos!

Bármely természetes szám nevezhető egész számnak, de egyetlen egész nem nevezhető természetes számnak. Arra a kérdésre válaszolva, hogy a negatív számok természetes számok-e, bátran ki kell mondanunk - nem, nem azok.

Nem pozitív és nem negatív egész számok

Adjunk néhány meghatározást.

6. definíció. Nem negatív egész számok

A nem negatív egész számok pozitív egészek és a szám nulla.

7. definíció. Nem pozitív egész számok

A nem pozitív egész számok negatív egész számok és a nulla szám.

Mint látható, a nulla szám nem pozitív és nem negatív.

Példák nemnegatív egész számokra: 52, 128, 0.

Példák nem pozitív egész számokra: - 52, - 128, 0.

A nem negatív szám nullánál nagyobb vagy azzal egyenlő szám. Ennek megfelelően a nem pozitív egész szám nullánál kisebb vagy azzal egyenlő.

A "nem pozitív szám" és a "nem negatív szám" kifejezéseket a rövidség kedvéért használjuk. Például ahelyett, hogy azt mondanánk, hogy az a szám nullánál nagyobb vagy azzal egyenlő egész szám, azt mondhatja: a nemnegatív egész szám.

Egész számok használata mennyiségi változások leírására

Mire használják az egész számokat? Először is, segítségükkel kényelmes leírni és meghatározni az objektumok mennyiségének változásait. Mondjunk egy példát.

Legyen bizonyos számú főtengely egy raktárban tárolva. Ha további 500 főtengely kerül a raktárba, akkor ezek száma növekedni fog. Az 500-as szám pontosan kifejezi az alkatrészek számának változását (növekedését). Ha ezután 200 alkatrészt vesznek ki a raktárból, akkor ez a szám fogja jellemezni a főtengelyek számának változását is. Ezúttal lefelé.

Ha semmit nem vesznek el a raktárból és semmit nem szállítanak ki, akkor a 0 szám azt jelzi, hogy az alkatrészek száma változatlan marad.

Az egész számok használatának nyilvánvaló kényelme a természetes számokkal szemben, hogy előjelük egyértelműen jelzi az érték változásának (növekedés vagy csökkenés) irányát.

A hőmérséklet 30 fokos csökkenése negatív egész számmal - 30, a 2 fokos növekedés - pozitív egész számmal 2 jellemezhető.

Adjunk egy másik példát egész számok használatára. Ezúttal képzeljük el, hogy 5 érmét kell adnunk valakinek. Akkor azt mondhatjuk, hogy van - 5 érménk. Az 5-ös szám az adósság nagyságát írja le, a mínusz jel pedig azt, hogy az érméket el kell adnunk.

Ha egy személynek 2 érmével tartozunk, a másiknak 3 érmével, akkor a teljes tartozás (5 érme) kiszámítható a negatív számok összeadásának szabályával:

2 + (- 3) = - 5

Ha hibát észlel a szövegben, jelölje ki, és nyomja meg a Ctrl+Enter billentyűkombinációt

Egész számok - ezek természetes számok, valamint ellentétük és nulla.

Egész számok— a természetes számok halmazának bővítése N, amelyet úgy kapunk, hogy hozzáadjuk N 0 és negatív számok, mint a − n. Az egész számok halmaza jelöli Z.

Az egész számok összege, különbsége és szorzata ismét egész számokat ad, i.e. egész számok gyűrűt alkotnak az összeadás és szorzás műveleteihez képest.

Egész számok a számegyenesen:

Hány egész szám? Hány egész szám? Nincs legnagyobb és legkisebb egész szám. Ez a sorozat végtelen. A legnagyobb és a legkisebb egész szám nem létezik.

A természetes számokat is nevezik pozitív egész számok, azaz a "természetes szám" és a "pozitív egész" kifejezés ugyanaz.

Sem a törtek, sem a tizedesjegyek nem egész számok. De vannak egész számokat tartalmazó törtek.

Példák egész számokra: -8, 111, 0, 1285642, -20051 stb.

Beszélő egyszerű nyelven, egész számok (∞... -4,-3,-2,-1,0,1,2,3,4...+ ∞) - egész számok sorozata. Vagyis azok, amelyeknek a tört része (()) egyenlő nullával. Nincs részvényük.

A természetes számok pozitív egész számok. Egész számok, példák: (1,2,3,4...+ ∞).

Műveletek egész számokkal.

1. Egész számok összege.

Két azonos előjelű egész szám összeadásához össze kell adni ezeknek a számoknak a moduljait, és a végső jelet az összeg elé kell tenni.

Példa:

(+2) + (+5) = +7.

2. Egész számok kivonása.

Két egész szám hozzáadásához különböző jelek, akkor a nagyobb szám modulusából ki kell vonni a kisebb szám modulusát, és a válasz elé kell tenni a nagyobb modulusszám előjelét.

Példa:

(-2) + (+5) = +3.

3. Egész számok szorzása.

Két egész szám szorzásához meg kell szorozni ezeknek a számoknak a modulusait, és pluszjelet (+) kell tenni a szorzat elé, ha az eredeti számok azonos előjelűek voltak, és mínuszjelet (-), ha különböztek.

Példa:

(+2) ∙ (-3) = -6.

Több szám szorzásakor a szorzat előjele pozitív lesz, ha a nem pozitív tényezők száma páros, és negatív, ha a nem pozitív tényezők száma páratlan.

Példa:

(-2) ∙ (+3) ∙ (-5) ∙ (-3) ∙ (+4) = -360 (3 nem pozitív tényező).

4. Egész számok felosztása.

Az egész számok elosztásához el kell osztani az egyik modulját a másik modulusával, és az eredmény elé kell tenni egy „+” jelet, ha a számok előjele megegyezik, és egy mínusz jelet, ha különböznek.

Példa:

(-12) : (+6) = -2.

Egész számok tulajdonságai.

Z nem zárt 2 egész szám osztása alatt ( például 1/2). Az alábbi táblázat az összeadás és szorzás néhány alapvető tulajdonságát mutatja bármely egész számra a, bÉs c.

Ingatlan	kiegészítés	szorzás
elkülönítés	a + b- egész	a × b- egész
asszociativitás	a + (b + c) = (a + b) + c	a × ( b × c) = (a × b) × c
kommutativitás	a + b = b + a	a × b = b × a
létezés semleges elem	a + 0 = a	a × 1 = a
létezés ellentétes elem	a + (−a) = 0	a ≠ ± 1 ⇒ 1/a nem egész szám
disztributivitás szorzási relatív kiegészítés	a × ( b + c) = (a × b) + (a × c)

A táblázatból arra következtethetünk Z egy kommutatív gyűrű, amelynek egysége összeadás és szorzás alatt van.

Szabványos osztás nem létezik az egész számok halmazán, de létezik az ún osztás maradékkal: minden egész számra aÉs b, b≠0, van egy egész számkészlet qÉs r, Mit a = bq + rÉs 0≤r<|b| , Ahol |b|- a szám abszolút értéke (modulusa). b. Itt a- osztható, b- elválasztó, q- magán, r- maradék.

1) Azonnal osztom, mivel mindkét szám 100%-ban osztható:

2) Osztom a fennmaradó nagy számokkal (és), mivel ezek egyenlően oszthatók (ugyanakkor nem bővítem - ez már közös osztó):

6 2 4 0 = 1 0 ⋅ 4 ⋅ 1 5 6

6 8 0 0 = 1 0 ⋅ 4 ⋅ 1 7 0

3) Elmegyek egyedül, és elkezdem nézni a számokat és. Mindkét szám pontosan osztható vele (vége páros számjegyekkel (ebben az esetben elképzeljük, hogyan, vagy osztható vele)):

4) Számokkal dolgozunk és. Vannak közös osztóik? Ez nem olyan egyszerű, mint az előző lépésekben, ezért egyszerűen lebontjuk őket egyszerű tényezőkre:

5) Amint látjuk, igazunk volt: és nincs közös osztójuk, és most szoroznunk kell.
GCD

2. feladat. Keresse meg a 345 és 324 számok gcd-jét

Itt nem találok gyorsan legalább egy közös osztót, ezért csak prímtényezőkre bontom (a lehető legkisebbre):

Pontosan, gcd, de eleinte nem ellenőriztem a vele való oszthatóság próbáját, és talán nem is kellett volna annyi műveletet csinálnom.

De ellenőrizted, igaz?

Amint látja, egyáltalán nem nehéz.

Least common multiple (LCM) - időt takarít meg, segít megoldani a problémákat nem szabványos módon

Tegyük fel, hogy két számod van – és. Mi a legkisebb szám, amivel osztható nyom nélkül(vagyis teljesen)? Nehéz elképzelni? Íme egy vizuális tipp az Ön számára:

Emlékszel, mit jelent a betű? Így van, csak egész számok. Tehát mi a legkisebb szám, ami elfér x helyére? :

Ebben az esetben.

Ebből az egyszerű példából több szabály is kirajzolódik.

Szabályok a NOC-ok gyors megtalálásához

1. szabály: Ha két természetes szám közül az egyik osztható egy másik számmal, akkor a két szám közül a nagyobb a legkisebb közös többszörösük.

Keresse meg a következő számokat:

• NOC (7;21)
• NOC (6;12)
• NOC (5;15)
• NOC (3;33)

Természetesen nehézség nélkül megbirkózott ezzel a feladattal, és megkapta a válaszokat - , és.

Kérjük, vegye figyelembe, hogy a szabályban KÉT számról beszélünk, ha több szám van, akkor a szabály nem működik.

Például az LCM (7;14;21) nem egyenlő 21-gyel, mivel nem osztható vele.

2. szabály: Ha két (vagy kettőnél több) szám másodprím, akkor a legkisebb közös többszörös egyenlő a szorzatukkal.

megtalálja NEM C a következő számokat:

• NOC (1;3;7)
• NOC (3;7;11)
• NOC (2;3;7)
• NOC (3;5;2)

számoltál? Íme a válaszok - , ; .

Amint érti, nem mindig lehet ilyen könnyen felvenni ugyanazt az x-et, ezért valamivel összetettebb számokhoz a következő algoritmus létezik:

Gyakoroljunk?

Keressük meg a legkisebb közös többszöröst - LCM (345; 234)

Bontsuk fel az egyes számokat:

Miért írtam rögtön?

Emlékezz az oszthatóság jeleire: osztható vele (az utolsó számjegy páros) és a számjegyek összege osztható vele.

Ennek megfelelően azonnal oszthatjuk vele, így írva.

Most felírjuk a leghosszabb lebontást egy sorra - a másodikra:

Adjuk hozzá az első bővítésből származó számokat, amelyek nem szerepelnek abban, amit kiírtunk:

Megjegyzés: mindent kiírtunk, kivéve, mert már megvan.

Most meg kell szoroznunk ezeket a számokat!

Keresse meg saját maga a legkisebb közös többszöröst (LCM).

Milyen válaszokat kaptál?

Íme, amit kaptam:

Mennyi időt töltött a kereséssel NEM C? Az időm 2 perc, tényleg tudom egy trükk, amelyet javaslok, hogy azonnal nyissa meg!

Ha nagyon figyelmes vagy, akkor valószínűleg észrevetted, hogy már megkerestük a megadott számokat GCDés átvehetnéd ezeknek a számoknak a faktorizálását abból a példából, leegyszerűsítve ezzel a feladatot, de ez még nem minden.

Nézze meg a képet, talán más gondolatok is eszébe jutnak:

Jól? Adok egy tippet: próbáld meg szorozni NEM CÉs GCD egymás között, és írják fel a szorzáskor megjelenő összes tényezőt. Sikerült? A végén egy ilyen láncot kell kapnia:

Nézze meg közelebbről: hasonlítsa össze a szorzót a hogyan és az elrendezéssel.

Milyen következtetést vonhatsz le ebből? Jobb! Ha az értékeket megszorozzuk NEM CÉs GCD egymás között, akkor ezeknek a számoknak a szorzatát kapjuk.

Ennek megfelelően számokkal és jelentéssel bír GCD(vagy NEM C), megtaláljuk NEM C(vagy GCD) e rendszer szerint:

1. Keresse meg a számok szorzatát:

2. A kapott terméket elosztjuk a miénkkel GCD (6240; 6800) = 80:

Ez minden.

Írjuk fel a szabályt általános formában:

Próbáld megtalálni GCD, ha ismert, hogy:

Sikerült? .

A negatív számok „hamis számok”, és az emberiség felismeri őket.

Amint már érted, ezek a természetes számokkal ellentétes számok, azaz:

Úgy tűnik, mi olyan különleges bennük?

De tény, hogy a negatív számok egészen a 19. századig „elnyerték” méltó helyüket a matematikában (addig a pillanatig hatalmas vita folyt arról, hogy léteznek-e vagy sem).

Maga a negatív szám a természetes számokkal végzett „kivonás” művelet miatt keletkezett.

Valóban, vonj le belőle, és kapsz egy negatív számot. Ezért gyakran nevezik a negatív számok halmazát "a természetes számok halmazának bővítése".

A negatív számokat sokáig nem ismerték fel az emberek.

Így az ókori Egyiptom, Babilon és az ókori Görögország - koruk fényei - nem ismerte fel a negatív számokat, és az egyenletben szereplő negatív gyökök esetén (például, mint a miénk), a gyökereket lehetetlennek minősítették.

A negatív számok először Kínában, majd a 7. században Indiában nyertek létjogosultságot.

Ön szerint mi az oka ennek az elismerésnek?

Így van, negatív számok kezdtek jelölni adósságok (egyébként - hiány).

Úgy gondolták, hogy a negatív számok átmeneti érték, ami ennek eredményeként pozitívra változik (azaz a pénz továbbra is visszakerül a hitelezőhöz). Brahmagupta indiai matematikus azonban már a negatív számokat is egyenlő alapon vette figyelembe a pozitívakkal.

Európában jóval később, talán egy évezreddel fedezték fel a negatív számok hasznosságát, valamint azt, hogy adósságokat jelölhetnek.

Az első említésre 1202-ben figyeltek fel Pisai Leonard „Abakusz könyvében” (azonnal leszögezem, hogy a könyv szerzőjének semmi köze a pisai ferde toronyhoz, de a Fibonacci-számok az ő munkái (a pisai Leonardo beceneve Fibonacci)).

Tehát a 17. században Pascal ezt hitte.

Szerinted mivel indokolta ezt?

Igaz, „semmi sem lehet kevesebb, mint a SEMMI”.

Ezeknek az időknek a visszhangja marad az a tény, hogy a negatív számot és a kivonási műveletet ugyanaz a szimbólum jelöli - a mínusz „-”. És az igazság: . A „ ” szám pozitív, amelyet kivonunk, vagy negatív, amelyhez összegezzük?... Valami a „mi előbb: a tyúk vagy a tojás?” sorozatból? Ez egy olyan sajátos matematikai filozófia.

A negatív számok az analitikus geometria megjelenésével biztosították létjogosultságukat, más szóval, amikor a matematikusok bevezették a számtengely fogalmát.

Ettől a pillanattól kezdve jött az egyenlőség. Azonban továbbra is több volt a kérdés, mint a válasz, például:

arány

Ezt az arányt „Arnaud-paradoxonnak” nevezik. Gondolj bele, mi ebben a kétséges?

Vitatkozzunk együtt, a "" több mint a "" igaz? Így a logika szerint az arány bal oldalának nagyobbnak kell lennie, mint a jobbnak, de egyenlők... Ez a paradoxon.

Ennek eredményeként a matematikusok egyetértettek abban, hogy Karl Gauss (igen, igen, ez ugyanaz, aki az összeget (vagy) számokat számolta ki) 1831-ben véget vetett ennek.

Azt mondta, hogy a negatív számoknak ugyanazok a jogai, mint a pozitívaknak, és az, hogy nem mindenre vonatkoznak, nem jelent semmit, hiszen a törtek sem vonatkoznak sok mindenre (nem történik meg, hogy egy ásó kátyút ásjon, nem lehet mozijegyet venni stb.).

A matematikusok csak a 19. században nyugszanak meg, amikor William Hamilton és Hermann Grassmann megalkotta a negatív számok elméletét.

Annyira ellentmondásosak, ezek a negatív számok.

Az „üresség” megjelenése, vagy a nulla életrajza.

A matematikában ez egy speciális szám.

Első pillantásra ez semmi: összeadás vagy kivonás - semmi sem fog változni, de csak hozzá kell adnia a jobb oldalhoz a „ ”-hoz, és a kapott szám többszöröse lesz az eredetinél.

A nullával való szorzással mindent semmivé változtatunk, a „semmivel” osztva viszont nem. Egyszóval a mágikus szám)

A nulla története hosszú és bonyolult.

2. évezredben a kínaiak írásaiban a nulla nyomát találták. és még korábban a maják között. A nulla szimbólum első használatát, ahogyan ma is, a görög csillagászok körében tapasztalták.

Számos változata létezik annak, hogy miért ezt a „semmi” megjelölést választották.

Egyes történészek hajlamosak azt hinni, hogy ez egy omikron, i.e. A semmit jelző görög szó első betűje az ouden. Egy másik változat szerint az „obol” szó (szinte értéktelen érme) adott életet a nulla szimbólumnak.

A nulla (vagy nulla) mint matematikai szimbólum először az indiánok körében jelenik meg(megjegyezzük, hogy a negatív számok ott kezdtek „fejlődni”).

A nulla rögzítésének első megbízható bizonyítéka 876-ból származik, és bennük a „ ” a szám összetevője.

A nulla is későn érkezett Európába - csak 1600-ban, és a negatív számokhoz hasonlóan ellenállásba ütközött (mit tehetsz, ilyenek az európaiak).

„A Zero-t gyakran utálják, régóta rettegnek, vagy akár be is tiltják.”- írja Charles Safe amerikai matematikus.

Így Abdul Hamid török ​​szultán a 19. század végén II. megparancsolta a cenzorainak, hogy töröljék ki a víz H2O képletét minden kémia tankönyvből, az „O” betűt nullának véve, és nem akarták, hogy a kezdőbetűit lejáratja a megvetett nullához való közelség.”

Az interneten megtalálható a következő mondat: „A nulla a legerősebb erő az Univerzumban, bármire képes! A nulla rendet teremt a matematikában, és káoszt is hoz benne.” Teljesen korrekt szempont :)

A szakasz összefoglalása és az alapképletek

Az egész számok halmaza 3 részből áll:

• természetes számok (az alábbiakban részletesebben is megvizsgáljuk őket);
• a természetes számokkal ellentétes számok;
• nulla - " "

Az egész számok halmazát jelöljük Z betű.

1. Természetes számok

A természetes számok olyan számok, amelyeket az objektumok megszámlálására használunk.

A természetes számok halmazát jelöljük N betű.

Az egész számokkal végzett műveleteknél meg kell találnia a GCD-t és az LCM-et.

Legnagyobb közös osztó (GCD)

A GCD megtalálásához a következőket kell tennie:

1. Bontsa fel a számokat prímtényezőkre (azokra a számokra, amelyek mással nem oszthatók, csak önmagukkal, vagy például másokkal stb.).
2. Írja le azokat a tényezőket, amelyek mindkét szám részét képezik!
3. Szaporítsd meg őket.

Legkevésbé közös többszörös (LCM)

A NOC megtalálásához szüksége lesz:

1. Oszd fel a számokat prímtényezőkre (ezt már nagyon jól tudod).
2. Írja le az egyik szám bővítésében szereplő tényezőket (jobb a leghosszabb láncot venni).
3. Adjuk hozzá a hiányzó tényezőket a fennmaradó számok bővítéséből.
4. Keresse meg a kapott tényezők szorzatát!

2. Negatív számok

Ezek a természetes számokkal ellentétes számok, azaz:

most hallani akarlak...

Remélem, értékelte az ebben a részben található rendkívül hasznos „trükköket”, és megértette, hogyan segítenek a vizsgán.

És ami még fontosabb - az életben. Nem beszélek róla, de hidd el, ez igaz. A gyors és hibamentes számolás képessége sok élethelyzetben megmenti Önt.

Most rajtad a sor!

Írj, használsz majd csoportosítási módszereket, oszthatósági teszteket, GCD-t és LCM-et a számításoknál?

Esetleg használtad már őket? Hol és hogyan?

Talán kérdései vannak. Vagy javaslatokat.

Írd meg kommentben, hogy tetszett a cikk.

És sok sikert a vizsgákhoz!