". Az első rész felvázolja azokat a rendelkezéseket, amelyek minimálisan szükségesek a kemometria megértéséhez, a második rész pedig azokat a tényeket tartalmazza, amelyeket tudnia kell a többváltozós elemzés módszereinek mélyebb megértéséhez. Az előadást Excel munkafüzetben készült példák illusztrálják Mátrix.xls amely ezt a dokumentumot kíséri.

A példákra mutató hivatkozások Excel objektumokként kerülnek a szövegbe. Ezek a példák absztrakt jellegűek, semmilyen módon nem kötődnek feladatokhoz. analitikai kémia. Valós Példák a mátrixalgebra kemometriai alkalmazását más, különféle kemometriai alkalmazásoknak szentelt szövegek tárgyalják.

Az analitikai kémiában végzett mérések többsége nem közvetlen, hanem közvetett. Ez azt jelenti, hogy a kísérletben a kívánt C analit értéke (koncentráció) helyett egy másik értéket kapunk. x(jel) kapcsolódik a C-hez, de nem egyenlő azzal, azaz. x(C) ≠ C. Általában a függőség típusa x(C) nem ismert, de szerencsére az analitikai kémiában a legtöbb mérés arányos. Ez azt jelenti, hogy a C koncentrációjaként a alkalommal, az X jel ugyanannyival fog növekedni., azaz. x(a C) = egy x(C). Ráadásul a jelek additívak is, így a két C 1 és C 2 koncentrációjú anyagot tartalmazó mintából érkező jel egyenlő lesz az egyes komponensekből érkező jelek összegével, azaz. x(C1 + C2) = x(C1)+ x(C2). Az arányosság és az additivitás együtt ad linearitás. A linearitás elvének szemléltetésére számos példát lehet hozni, de elég csak megemlíteni a két legszembetűnőbb példát - a kromatográfiát és a spektroszkópiát. Az analitikai kémia kísérletének második jellemzője az többcsatornás. A modern analitikai berendezések egyidejűleg számos csatorna jelét mérik. Például a fényáteresztés intenzitását egyszerre több hullámhosszra mérik, pl. hatótávolság. Ezért a kísérletben sokféle jellel van dolgunk x 1 , x 2 ,...., x n, amely a vizsgált rendszerben jelenlévő anyagok C 1 ,C 2 , ..., C m koncentrációkészletét jellemzi.

Rizs. 1 Spectra

Tehát az analitikus kísérletet a linearitás és a többdimenziósság jellemzi. Ezért célszerű a kísérleti adatokat vektoroknak és mátrixoknak tekinteni, és ezeket a mátrixalgebra apparátusával manipulálni. E megközelítés eredményességét szemlélteti a -ban bemutatott példa, amely három spektrumot mutat 200 hullámhosszra 4000 és 4796 cm–1 között. Első ( x 1) és második ( x 2) a spektrumokat olyan standard mintákra kaptuk, amelyekben két A és B anyag koncentrációja ismert: az első mintában [A] = 0,5, [B] = 0,1, és a második mintában [A] = 0,2, [ B] = 0,6. Mit lehet mondani egy új, ismeretlen mintáról, amelynek spektruma meg van jelölve x 3 ?

Tekintsünk három kísérleti spektrumot x 1 , x 2 és x A 3. ábra három, 200-as dimenziójú vektorként. A lineáris algebra segítségével ez könnyen kimutatható x 3 = 0.1 x 1 +0.3 x 2, tehát a harmadik minta nyilvánvalóan csak az A és B anyagokat tartalmazza [A] = 0,5×0,1 + 0,2×0,3 = 0,11 és [B] = 0,1×0,1 + 0,6×0,3 = 0,19 koncentrációban.

1. Alapvető információk

1.1 Mátrixok

Mátrix téglalap alakú számtáblázatnak nevezzük például

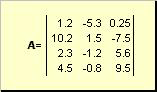
Rizs. 2 Mátrix

A mátrixokat félkövér nagybetűkkel jelöljük ( A), és ezek elemei - a megfelelő kisbetűkkel indexekkel, azaz. a ij . Az első index a sorokat, a második pedig az oszlopokat számozza. A kemometriában szokás az index maximális értékét ugyanazzal a betűvel jelölni, mint magát az indexet, de nagybetűkkel. Ezért a mátrix Aúgy is írható, hogy ( a ij , én = 1,..., én; j = 1,..., J). A példamátrixhoz én = 4, J= 3 és a 23 = −7.5.

Számpár énÉs J a mátrix dimenziójának nevezzük, és így jelöljük én× J. A kemometriai mátrixra példa egy spektrumkészlet, amelyet a következőre kaptunk én minták rajta J hullámhosszak.

1.2. A legegyszerűbb műveletek mátrixokkal

A mátrixok képesek szorozzuk meg számokkal. Ebben az esetben minden elemet megszorozunk ezzel a számmal. Például -

Rizs. 3 Egy mátrix szorzása egy számmal

Két azonos méretű mátrix lehet elemenként hajtogatniÉs kivonni. Például,

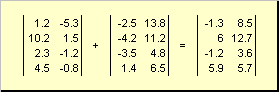
Rizs. 4 Mátrix összeadás

A számmal való szorzás és az összeadás eredményeként azonos méretű mátrixot kapunk.

A nulla mátrix egy nullákból álló mátrix. Ki van jelölve O. Ez nyilvánvaló A+O = A, A−A = Oés 0 A = O.

A mátrix képes átültetni. A művelet során a mátrix megfordul, azaz sorok és oszlopok felcserélődnek. Az átültetést kötőjel jelzi, A" vagy index A t . Így ha A = {a ij , én = 1,..., én; j = 1,...,J), Ez A t = ( a ji , j = 1,...,J; i = 1,..., én). Például

Rizs. 5 Mátrix transzpozíció

Nyilvánvaló, hogy ( A t) t = A, (A+B) t = A t+ B t .

1.3. Mátrixszorzás

A mátrixok képesek szaporodnak, de csak akkor, ha megfelelő méretekkel rendelkeznek. Hogy ez miért van így, az a definícióból kiderül. Mátrix termék A, dimenzió én× K, és mátrixok B, dimenzió K× J, mátrixnak nevezzük C, dimenzió én× J, melynek elemei számok

Így a termékhez AB szükséges, hogy a bal oldali mátrix oszlopainak száma A egyenlő volt a jobb oldali mátrix sorainak számával B. Példa a mátrix termékre -

6. ábra Mátrixok szorzata

A mátrixszorzás szabálya a következőképpen fogalmazható meg. Egy mátrix elemének megtalálása C a kereszteződésben állva én-edik sor és j-adik oszlop ( c ij) elemet elemenként kell szorozni én-az első mátrix sora A tovább j-a második mátrix oszlopa Bés összeadjuk az összes eredményt. Tehát a bemutatott példában a harmadik sor és a második oszlop elemét a harmadik sor elemenkénti szorzatainak összegeként kapjuk meg. Aés a második oszlop B

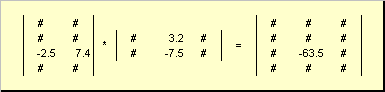
7. ábra Mátrixok szorzatának eleme

A mátrixok szorzata a sorrendtől függ, pl. AB ≠ BA, legalábbis méretbeli okokból. Azt mondják, hogy nem kommutatív. A mátrixok szorzata azonban asszociatív. Ez azt jelenti ABC = (AB)C = A(időszámításunk előtt). Sőt, elosztó is, i.e. A(B+C) = AB+AC. Ez nyilvánvaló AO = O.

1.4. Négyzetes mátrixok

Ha egy mátrix oszlopainak száma egyenlő a sorok számával ( én = J=N), akkor egy ilyen mátrixot négyzetnek neveznek. Ebben a részben csak az ilyen mátrixokat fogjuk figyelembe venni. Ezen mátrixok közül kiemelhetünk speciális tulajdonságokkal rendelkező mátrixokat.

Magányos mátrix (jelölve énés néha E) egy olyan mátrix, amelyben minden elem egyenlő nullával, kivéve az átlósakat, amelyek egyenlőek 1-gyel, azaz.

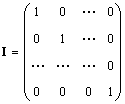
Magától értetődően AI = IA = A.

A mátrix az ún átlós, ha minden eleme, kivéve az átlósakat ( a ii) egyenlők nullával. Például

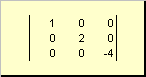
Rizs. 8 Átlós mátrix

Mátrix A csúcsnak nevezték háromszög alakú, ha az átló alatt fekvő összes eleme egyenlő nullával, azaz. a ij= 0, at én>j. Például

Rizs. 9 Felső háromszögmátrix

Az alsó háromszögmátrixot hasonlóan határozzuk meg.

Mátrix A hívott szimmetrikus, Ha A t = A. Más szavakkal a ij = a ji. Például

Rizs. 10 Szimmetrikus mátrix

Mátrix A hívott ortogonális, Ha

A t A = AA t = én.

A mátrix az ún Normál Ha

1.5. Nyom és meghatározó

Következő négyzetmátrix A(jelölve Tr( A) vagy Sp( A)) az átlós elemeinek összege,

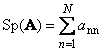
Például,

Rizs. 11 Mátrix nyom

Ez nyilvánvaló

Sp(α A) = α Sp( A) És

Sp( A+B) = Sp( A)+ Sp( B).

Meg lehet mutatni, hogy

Sp( A) = Sp( A t), Sp( én) = N,

és azt is

Sp( AB) = Sp( BA).

A négyzetmátrix másik fontos jellemzője az döntő(jelölése det( A)). A determináns meghatározása in általános eset meglehetősen bonyolult, ezért kezdjük a legegyszerűbb lehetőséggel - a mátrixszal A méret (2×2). Akkor

Egy (3×3) mátrix esetén a determináns egyenlő lesz

Mátrix esetén ( N× N) a determinánst 1 2 3 ... összegként számítjuk ki... N= N! kifejezések, amelyek mindegyike egyenlő

Indexek k 1 , k 2 ,..., k N az összes lehetséges rendezett permutációt jelenti r számok a halmazban (1, 2, ... , N). A mátrix determináns kiszámítása összetett eljárás, amelyet a gyakorlatban speciális programok segítségével hajtanak végre. Például,

Rizs. 12 Mátrix determináns

Csak a nyilvánvaló tulajdonságokat jegyezzük meg:

det( én) = 1, det( A) = det( A t),

det( AB) = det( A)det( B).

1.6. Vektorok

Ha a mátrixnak csak egy oszlopa van ( J= 1), akkor egy ilyen objektumot hívunk vektor. Pontosabban egy oszlopvektor. Például

Egy sorból álló mátrixok is szóba jöhetnek például

Ez az objektum is vektor, de sor vektor. Az adatok elemzésekor fontos megérteni, hogy mely vektorokkal van dolgunk - oszlopokkal vagy sorokkal. Tehát az egy mintára felvett spektrum sorvektornak tekinthető. Ekkor a spektrális intenzitások halmazát valamilyen hullámhosszon minden mintára oszlopvektorként kell kezelni.

Egy vektor dimenziója az elemeinek száma.

Nyilvánvaló, hogy bármely oszlopvektor transzpozícióval átalakítható sorvektorrá, azaz.

Azokban az esetekben, amikor egy vektor alakja nincs konkrétan megadva, hanem egyszerűen egy vektort mondanak, akkor oszlopvektort jelentenek. Ezt a szabályt mi is betartjuk. Egy vektort kisbetűs, közvetlen félkövér betűvel jelölünk. A nulla vektor olyan vektor, amelynek minden eleme nulla. Meg van jelölve 0 .

1.7. A legegyszerűbb műveletek vektorokkal

A vektorok a mátrixokhoz hasonlóan összeadhatók és számokkal szorozhatók. Például,

Rizs. 13 Műveletek vektorokkal

Két vektor xÉs y hívott kollineáris, ha van olyan α szám, hogy

1.8. A vektorok szorzatai

Két azonos dimenziójú vektor N szaporítható. Legyen két vektor x = (x 1 , x 2 ,...,x N) t és y = (y 1 , y 2 ,...,y N) t. A "sorról oszlopra" szorzási szabálytól függően két szorzatot készíthetünk belőlük: x t yÉs xy t . Első munka

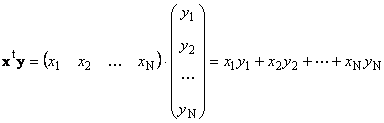
hívott skalár vagy belső. Ennek eredménye egy szám. Használja a jelölést is ( x,y)= x t y. Például,

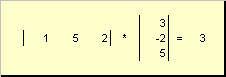
Rizs. 14 Belső (skaláris) szorzat

Második munka

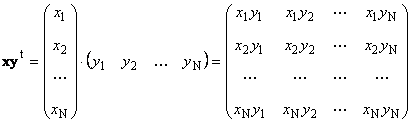
hívott külső. Ennek eredménye egy dimenziómátrix ( N× N). Például,

Rizs. 15 Külső termék

Olyan vektorokat nevezünk, amelyek skaláris szorzata nullával egyenlő ortogonális.

1.9. Vektor norma

Egy vektor önmagával való skaláris szorzatát skalárnégyzetnek nevezzük. Ezt az értéket

négyzetet határoz meg hossz vektor x. A hosszúság jelölésére (más néven a norma vektor) a jelölést használjuk

Például,

Rizs. 16 Vektor norm

Mértékegység hosszvektor (|| x|| = 1) normalizáltnak nevezzük. Nem nulla vektor ( x ≠ 0 ) normalizálható, ha elosztjuk a hosszával, azaz. x = ||x|| (x/||x||) = ||x|| e. Itt e = x/||x|| egy normalizált vektor.

A vektorokat ortonormálisnak nevezzük, ha mindegyik normalizált és páronként merőleges.

1.10. Szög vektorok között

A skaláris szorzat meghatározza és sarokφ két vektor között xÉs y

Ha a vektorok ortogonálisak, akkor cosφ = 0 és φ = π/2, ha pedig kollineárisak, akkor cosφ = 1 és φ = 0.

1.11. Egy mátrix vektoros ábrázolása

Mindegyik mátrix A méret én× J vektorok halmazaként ábrázolható

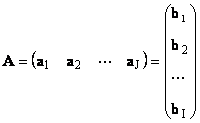
Itt minden vektor a j van j-edik oszlop és sor vektor b én van én-a mátrix sora A

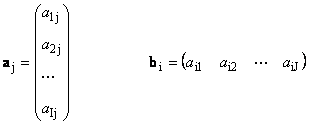
1.12. Lineárisan függő vektorok

Azonos dimenziójú vektorok ( N) a mátrixokhoz hasonlóan összeadható és szorozható egy számmal. Az eredmény egy azonos dimenziójú vektor. Legyen több azonos dimenziójú vektor x 1 , x 2 ,...,x K és ugyanannyi szám α α 1 , α 2 ,...,α K. Vektor

y= α 1 x 1 + α 2 x 2 +...+α K x K

hívott lineáris kombináció vektorok x k .

Ha vannak olyan nem nulla számok α k ≠ 0, k = 1,..., K, Mit y = 0 , akkor egy ilyen vektorhalmaz x k hívott lineárisan függő. Egyébként a vektorokat lineárisan függetlennek nevezzük. Például vektorok x 1 = (2, 2) t és x 2 = (−1, −1) t lineárisan függő, hiszen x 1 +2x 2 = 0

1.13. Mátrix rang

Fontolja meg egy sor K vektorok x 1 , x 2 ,...,x K méretek N. Ennek a vektorrendszernek a rangja a lineárisan független vektorok maximális száma. Például a készletben

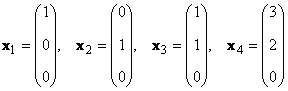
csak két lineárisan független vektor van például x 1 és x 2, tehát a rangja 2.

Nyilvánvalóan, ha több vektor van a halmazban, mint a dimenziójuk ( K>N), akkor szükségszerűen lineárisan függenek.

Mátrix rang(jelöli rang( A)) annak a vektorrendszernek a rangja, amelyből áll. Bár bármely mátrix kétféleképpen ábrázolható (oszlopvektorok vagy sorvektorok), ez nem befolyásolja a rangértéket, mivel

1.14. inverz mátrix

négyzetmátrix A nem degeneráltnak nevezzük, ha egyedi fordított mátrix A-1 , a feltételek határozzák meg

AA −1 = A −1 A = én.

Az inverz mátrix nem létezik minden mátrixra. A nem-degeneráció szükséges és elégséges feltétele

det( A) ≠ 0 vagy rang( A) = N.

A mátrix inverzió egy összetett eljárás, amelyhez speciális programok vannak. Például,

Rizs. 17 Mátrix inverzió

Képleteket adunk a legegyszerűbb esetekre - 2 × 2 mátrixok

Ha mátrixok AÉs B akkor nem degeneráltak

(AB) −1 = B −1 A −1 .

1.15. Pszeudo-inverz mátrix

Ha a mátrix A degenerált és az inverz mátrix nem létezik, akkor bizonyos esetekben használható pszeudo-inverz mátrix, amely ilyen mátrixként van definiálva A+ az

AA + A = A.

A pszeudo-inverz mátrix nem az egyetlen, és formája az építési módtól függ. Például egy téglalap alakú mátrixhoz használhatja a Moore-Penrose módszert.

Ha az oszlopok száma kisebb, mint a sorok száma, akkor

A + =(A t A) −1 A t

Például,

Rizs. 17a Pszeudomátrix inverzió

Ha az oszlopok száma nagyobb, mint a sorok száma, akkor

A + =A t( AA t) −1

1.16. Vektor szorzása mátrixszal

Vektor x mátrixszal szorozható A megfelelő méret. Ebben az esetben az oszlopvektort a jobb oldalon megszorozzuk Fejsze, és a vektorkarakter a bal oldalon található x t A. Ha a vektor dimenziója J, és a mátrix dimenziója én× J akkor az eredmény egy dimenzióvektor én. Például,

Rizs. 18 Vektor-mátrix szorzás

Ha a mátrix A- négyzet ( én× én), majd a vektort y = Fejsze mérete megegyezik a x. Ez nyilvánvaló

A(α 1 x 1 + α 2 x 2) = α 1 Fejsze 1 + α 2 Fejsze 2 .

Ezért a mátrixok vektorok lineáris transzformációinak tekinthetők. Különösen x = x, Ökör = 0 .

2. További információk

2.1. Lineáris egyenletrendszerek

Hadd A- mátrix mérete én× J, A b- méretvektor J. Tekintsük az egyenletet

Fejsze = b

a vektorhoz képest x, méretek én. Lényegében ez egy rendszer én lineáris egyenletek Val vel J ismeretlen x 1 ,...,x J. A megoldás akkor és csak akkor létezik

rang( A) = rang( B) = R,

Ahol B a kiterjesztett dimenziós mátrix én×( J+1), amely a mátrixból áll A, oszloppal párnázott b, B = (A b). Ellenkező esetben az egyenletek inkonzisztensek.

Ha R = én = J, akkor a megoldás egyedi

x = A −1 b.

Ha R < én, akkor sokféle megoldás létezik, amelyek lineáris kombinációval fejezhetők ki J−R vektorok. Rendszer homogén egyenletek Fejsze = 0 négyzetmátrixszal A (N× N) van egy nem triviális megoldása ( x ≠ 0 ) akkor és csak akkor, ha det( A) = 0. Ha R= rang( A)<N, akkor vannak N−R lineárisan független megoldások.

2.2. Bilineáris és másodfokú formák

Ha A egy négyzetes mátrix, és xÉs y- a megfelelő dimenzió vektorai, majd az alak skaláris szorzata x t Ay hívott bilineáris a mátrix által meghatározott alakzat A. Nál nél x = y kifejezés x t Fejsze hívott négyzetes forma.

2.3. Pozitív határozott mátrixok

négyzetmátrix A hívott pozitív határozott, ha bármely nem nulla vektorra x ≠ 0 ,

x t Fejsze > 0.

A negatív (x t Fejsze < 0), nem negatív (x t Fejsze≥ 0) és nem pozitív (x t Fejsze≤ 0) bizonyos mátrixok.

2.4. Cholesky-bomlás

Ha a szimmetrikus mátrix A pozitív határozott, akkor létezik egy egyedi háromszögmátrix U pozitív elemekkel, amihez

A = U t U.

Például,

Rizs. 19 Cholesky-bontás

2.5. poláris bomlás

Hadd A egy nem degenerált dimenziós négyzetmátrix N× N. Aztán van egy egyedi poláris teljesítmény

A = SR,

Ahol S egy nem negatív szimmetrikus mátrix, és R egy ortogonális mátrix. mátrixok SÉs R kifejezetten definiálható:

S 2 = AA t vagy S = (AA t) ½ és R = S −1 A = (AA t) −½ A.

Például,

Rizs. 20 Poláris bomlás

Ha a mátrix A degenerált, akkor a dekompozíció nem egyedi - nevezetesen: S még mindig egyedül, de R sokan lehetnek. A poláris dekompozíció egy mátrixot jelent A kompresszió/nyújtás kombinációként Sés fordul R.

2.6. Sajátvektorok és sajátértékek

Hadd A egy négyzetes mátrix. Vektor v hívott saját vektor mátrixok A, Ha

Av = λ v,

ahol a λ számot hívják sajátérték mátrixok A. Így a mátrix által végrehajtott transzformáció A vektor felett v, egyszerű nyújtásra vagy összenyomásra redukálódik λ tényezővel. A sajátvektort a szorzásig az α ≠ 0 állandóval határozzuk meg, azaz. Ha v egy sajátvektor, akkor α v egyben sajátvektor is.

2.7. Sajátértékek

A mátrixnál A, méret ( N× N) nem lehet nagyobb, mint N sajátértékek. Megelégednek karakterisztikus egyenlet

det( A − λ én) = 0,

lény algebrai egyenlet N-edik sorrend. Egy 2×2-es mátrix esetében a karakterisztikus egyenletnek ilyen alakja van

Például,

Rizs. 21 Sajátértékek

Sajátértékek halmaza λ 1 ,..., λ N mátrixok A hívott spektrum A.

A spektrum különféle tulajdonságokkal rendelkezik. Különösen

det( A) = λ 1×...×λ N, Sp( A) = λ 1 +...+λ N.

Egy tetszőleges mátrix sajátértékei lehetnek komplex számok, de ha a mátrix szimmetrikus ( A t = A), akkor a sajátértékei valósak.

2.8. Sajátvektorok

A mátrixnál A, méret ( N× N) nem lehet nagyobb, mint N sajátvektorok, amelyek mindegyike a saját értékének felel meg. A sajátvektor meghatározásához v n meg kell oldania egy homogén egyenletrendszert

(A − λ n én)v n = 0 .

Van egy nem triviális megoldása, mert det( A-λ n én) = 0.

Például,

Rizs. 22 sajátvektor

A szimmetrikus mátrix sajátvektorai ortogonálisak.

A négyzetes mátrix sajátvektora az, amelyet egy adott mátrixszal megszorozva kollineáris vektort kapunk. Egyszerű szavakkal, amikor egy mátrixot megszorozunk egy sajátvektorral, az utóbbi ugyanaz marad, de megszorozzuk valamilyen számmal.

Meghatározás

A sajátvektor egy nem nulla V vektor, amely egy M négyzetmátrixszal megszorozva önmaga lesz, megnövelve valamilyen λ számmal. Algebrai jelölésben ez így néz ki:

M × V = λ × V,

ahol λ az M mátrix sajátértéke.

Nézzünk egy numerikus példát. Az írás megkönnyítése érdekében a mátrixban szereplő számokat pontosvessző választja el egymástól. Tegyük fel, hogy van egy mátrixunk:

• M=0; 4;
• 6; 10.

Szorozzuk meg egy oszlopvektorral:

• V = -2;

Ha egy mátrixot megszorozunk egy oszlopvektorral, akkor egy oszlopvektort is kapunk. Szigorú matematikai nyelven a 2 × 2-es mátrix oszlopvektorral való szorzásának képlete a következőképpen nézne ki:

• M × V = M11 × V11 + M12 × V21;
• M21 x V11 + M22 x V21.

Az M11 az M mátrix első sorban és első oszlopában lévő elemét jelenti, M22 pedig a második sorban és a második oszlopban található elemet. A mi mátrixunknál ezek az elemek M11 = 0, M12 = 4, M21 = 6, M22 10. Oszlopvektor esetén ezek az értékek V11 = –2, V21 = 1. E képlet szerint a következőt kapjuk négyzetmátrix vektorral való szorzatának eredménye:

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2.

A kényelem kedvéért az oszlopvektort egy sorba írjuk. Tehát a négyzetmátrixot megszoroztuk a (-2; 1) vektorral, így a (4; -2) vektort kaptuk. Nyilvánvaló, hogy ez ugyanaz a vektor, megszorozva λ = -2-vel. A lambda ebben az esetben a mátrix egy sajátértékét jelöli.

A mátrix sajátvektora egy kollineáris vektor, vagyis egy olyan objektum, amely nem változtatja meg a térbeli helyzetét, ha mátrixszal megszorozzuk. A vektoralgebrában a kollinearitás fogalma hasonló a geometriai párhuzamosság fogalmához. A geometriai értelmezésben a kollineáris vektorok párhuzamosan irányított, különböző hosszúságú szakaszok. Eukleidész kora óta tudjuk, hogy egyetlen egyenesnek végtelen számú vele párhuzamos egyenese van, ezért logikus azt feltételezni, hogy minden mátrix végtelen számú sajátvektorral rendelkezik.

Az előző példából látható, hogy mind a (-8; 4), mind a (16; -8), mind a (32, -16) lehet sajátvektor. Mindezek kollineáris vektorok, amelyek megfelelnek a λ = -2 sajátértéknek. Ha az eredeti mátrixot megszorozzuk ezekkel a vektorokkal, akkor is egy olyan vektort kapunk, amely 2-szer tér el az eredetitől. Éppen ezért a sajátvektor keresési feladatainak megoldása során csak lineárisan független vektorobjektumokat kell megtalálni. Leggyakrabban egy n × n mátrixhoz n-edik számú sajátvektor van. Számológépünk másodrendű négyzetmátrixok elemzésére készült, így szinte mindig két sajátvektor fog megjelenni, kivéve, ha azok egybeesnek.

A fenti példában előre tudtuk az eredeti mátrix sajátvektorát, és vizuálisan meghatároztuk a lambda számot. A gyakorlatban azonban minden fordítva történik: az elején sajátértékek vannak, és csak azután sajátvektorok.

Megoldási algoritmus

Nézzük meg újra az eredeti M mátrixot, és próbáljuk meg megtalálni mindkét sajátvektorát. Tehát a mátrix így néz ki:

• M=0; 4;
• 6; 10.

Először meg kell határoznunk a λ sajátértéket, amelyhez ki kell számítanunk a következő mátrix determinánsát:

• (0 − λ); 4;
• 6; (10 − λ).

Ez a mátrixúgy kapjuk, hogy a főátló elemeiből kivonjuk az ismeretlen λ-t. A determinánst a standard képlet határozza meg:

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

Mivel a vektorunk nem lehet nulla, a kapott egyenletet lineárisan függőnek tekintjük, és a detA determinánsunkat nullával egyenlővé tesszük.

(0 − λ) × (10 − λ) − 24 = 0

Nyissuk ki a zárójeleket és kapjuk meg a mátrix karakterisztikus egyenletét:

λ 2 − 10λ − 24 = 0

Ez szabvány másodfokú egyenlet, amelyet a diszkrimináns szempontjából kell megoldani.

D \u003d b 2 - 4ac \u003d (-10) × 2 - 4 × (-1) × 24 = 100 + 96 \u003d 196

A diszkrimináns gyöke sqrt(D) = 14, tehát λ1 = -2, λ2 = 12. Most minden lambda értékhez meg kell találnunk egy sajátvektort. Adjuk meg a rendszer együtthatóit λ = -2 esetén.

• M − λ × E = 2; 4;
• 6; 12.

Ebben a képletben E az azonosságmátrix. A kapott mátrix alapján lineáris egyenletrendszert állítunk össze:

2x + 4y = 6x + 12y

ahol x és y a sajátvektor elemei.

Gyűjtsük össze az összes X-et a bal oldalon és az összes Y-t a jobb oldalon. Nyilvánvalóan - 4x = 8 év. Osszuk el a kifejezést -4-gyel, és kapjuk x = -2y. Most meghatározhatjuk a mátrix első sajátvektorát az ismeretlenek tetszőleges értékével (emlékezzünk a lineárisan függő sajátvektorok végtelenjére). Tegyük fel, hogy y = 1, majd x = -2. Ezért az első sajátvektor így néz ki: V1 = (–2; 1). Vissza a cikk elejére. Ezzel a vektorobjektummal szoroztuk meg a mátrixot, hogy bemutassuk a sajátvektor fogalmát.

Most keressük meg a λ = 12 sajátvektorát.

• M - λ × E = -12; 4
• 6; -2.

Állítsuk össze ugyanazt a lineáris egyenletrendszert;

• -12x + 4y = 6x - 2y
• -18x = -6 év
• 3x=y.

Most vegyük x = 1, tehát y = 3. Így a második sajátvektor így néz ki, mint V2 = (1; 3). Ha az eredeti mátrixot megszorozzuk ezzel a vektorral, az eredmény mindig ugyanaz a vektor lesz szorozva 12-vel. Ezzel befejeződik a megoldási algoritmus. Most már tudja, hogyan kell manuálisan meghatározni egy mátrix sajátvektorát.

• döntő;
• trace, azaz a főátlón lévő elemek összege;
• rang, azaz a lineárisan független sorok/oszlopok maximális száma.

A program a fenti algoritmus szerint működik, minimalizálva a megoldási folyamatot. Fontos kiemelni, hogy a programban a lambdát "c" betű jelöli. Nézzünk egy numerikus példát.

Program példa

Próbáljunk meg sajátvektorokat definiálni a következő mátrixhoz:

• M=5; 13;
• 4; 14.

Írjuk be ezeket az értékeket a számológép celláiba, és kapjuk meg a választ a következő formában:

• Mátrix rang: 2;
• Mátrix determináns: 18;
• Mátrix nyom: 19;
• Sajátvektor számítás: c 2 − 19.00c + 18.00 (karakteregyenlet);
• Sajátvektor számítás: 18 (első lambda érték);
• Sajátvektor számítás: 1 (második lambda érték);
• Az 1. vektor egyenletrendszere: -13x1 + 13y1 = 4x1 − 4y1;
• 2. vektor egyenletrendszer: 4x1 + 13y1 = 4x1 + 13y1;
• 1. sajátvektor: (1; 1);
• 2. sajátvektor: (-3,25; 1).

Így két lineárisan független sajátvektort kaptunk.

Következtetés

Lineáris algebra és analitikus geometria- standard tantárgyak bármely műszaki szakos pályakezdő számára. Nagyszámú A vektorok és mátrixok ijesztő, és ilyen nehézkes számításokban könnyű hibázni. Programunk lehetővé teszi a diákok számára, hogy ellenőrizzék számításaikat, vagy automatikusan megoldják a sajátvektor megtalálásának problémáját. Katalógusunkban további lineáris algebrai számológépek találhatók, használja őket tanulmányaiban vagy munkájában.

Meghatározás 9.3. Vektor x hívott saját vektor mátrixok A ha van ilyen szám λ, hogy az egyenlőség fennáll: A x= λ x, vagyis az arra való jelentkezés eredménye x mátrix által adott lineáris transzformáció A, ennek a vektornak a szorzata a számmal λ . Maga a szám λ hívott saját szám mátrixok A.

Behelyettesítés képletekre (9.3) x` j = λx j , egyenletrendszert kapunk a sajátvektor koordinátáinak meghatározására:

. (9.5)

Ennek a lineáris homogén rendszernek csak akkor lesz nem triviális megoldása, ha fő determinánsa 0 (Cramer-szabály). Ha ezt a feltételt a következő formában írja be:

egyenletet kapunk a sajátértékek meghatározására λ hívott karakterisztikus egyenlet. Röviden a következőképpen ábrázolható:

| A-λE | = 0, (9.6)

mivel bal oldala a mátrix meghatározója A-λE. Polinom viszonylatban λ | A-λE| hívott karakterisztikus polinom mátrixok A.

A karakterisztikus polinom tulajdonságai:

1) A lineáris transzformáció karakterisztikus polinomja nem függ a bázis megválasztásától. Bizonyíték. (lásd (9.4)), de ennélfogva, . Így nem függ az alap megválasztásától. Ezért és | A-λE| nem változik az új alapra való áttéréskor.

2) Ha a mátrix A lineáris transzformáció az szimmetrikus(azok. a ij = a ji), majd minden gyökér karakterisztikus egyenlet(9.6) valós számok.

A sajátértékek és sajátvektorok tulajdonságai:

1) Ha sajátvektorok közül választunk bázist x 1, x 2, x 3 a sajátértékeknek megfelelő λ 1 , λ 2 , λ 3 mátrixok A, akkor ezen az alapon az A lineáris transzformációnak van egy átlós mátrixa:

(9.7) Ennek a tulajdonságnak a bizonyítása a sajátvektorok definíciójából következik.

2) Ha a transzformáció sajátértékei A különböznek, akkor a hozzájuk tartozó sajátvektorok lineárisan függetlenek.

3) Ha a mátrix karakterisztikus polinomja A három különböző gyöke van, akkor valamilyen alapon a mátrix Aátlós alakja van.

Keressük meg a mátrix sajátértékeit és sajátvektorait. Készítsük el a karakterisztikus egyenletet: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ³ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

Keresse meg az egyes talált értékekhez tartozó sajátvektorok koordinátáit! λ. A (9.5)-ből az következik, hogy ha x (1) ={x 1, x 2, x 3) a megfelelő sajátvektor λ 1 = -2 tehát

együttműködésen alapuló, de határozatlan rendszer. Megoldása így írható fel x (1) ={a,0,-a), ahol a tetszőleges szám. Különösen, ha szüksége van arra, hogy | x (1) |=1, x (1) =

Behelyettesítés a rendszerbe (9.5) λ 2 =3, kapunk egy rendszert a második sajátvektor koordinátáinak meghatározására - x (2) ={y1,y2,y3}:

, ahol x (2) ={b,-b,b) vagy feltéve, hogy | x (2) |=1, x (2) =

Mert λ 3 = 6 keresse meg a sajátvektort x (3) ={z1, z2, z3}:

, x (3) ={c,2c, c) vagy a normalizált változatban

x (3) = Ez látható x (1) x (2) = ab-ab= 0, x (1) x (3) = ac-ac= 0, x (2) x (3) = időszámításunk előtt- 2bc + bc= 0. Így ennek a mátrixnak a sajátvektorai páronként ortogonálisak.

10. előadás

Másodfokú formák és kapcsolatuk szimmetrikus mátrixokkal. A szimmetrikus mátrix sajátvektorainak és sajátértékeinek tulajdonságai. Másodfokú forma redukálása kanonikus formává.

Meghatározás 10.1.másodfokú forma valós változók x 1, x 2,…, x n egy másodfokú polinomot nevezünk ezekre a változókra vonatkozóan, amely nem tartalmaz szabad tagot és elsőfokú tagokat.

Példák másodfokú alakzatokra:

(n = 2),

(n = 3). (10.1)

Emlékezzünk vissza a szimmetrikus mátrix utolsó előadásban adott definíciójára:

Meghatározás 10.2. A négyzetmátrixot ún szimmetrikus, ha , vagyis ha a főátlóhoz képest szimmetrikus mátrixelemek egyenlőek.

A szimmetrikus mátrix sajátértékeinek és sajátvektorainak tulajdonságai:

1) A szimmetrikus mátrix minden sajátértéke valós.

Bizonyíték (azért n = 2).

Hagyja a mátrixot Aúgy néz ki, mint a: . Készítsük el a karakterisztikus egyenletet:

(10.2) Keresse meg a diszkriminánst:

Ezért az egyenletnek csak valódi gyökerei vannak.

2) A szimmetrikus mátrix sajátvektorai ortogonálisak.

Bizonyíték (azért n= 2).

A és a sajátvektorok koordinátáinak meg kell felelniük az egyenleteknek.

Az átlós típusú mátrixok a legegyszerűbben vannak elrendezve. Felmerül a kérdés, hogy lehet-e olyan bázist találni, amelyben egy lineáris operátor mátrixának diagonális alakja lenne. Ilyen alap létezik.
Legyen adott egy R n lineáris tér és egy benne ható A lineáris operátor; ebben az esetben az A operátor magába veszi az R n-t, vagyis A:R n → R n .

Meghatározás. Egy nem nulla vektort az A operátor sajátvektorának nevezünk, ha az A operátor egy vele kollineáris vektorrá alakul át, azaz . A λ számot a sajátvektornak megfelelő A operátor sajátértékének vagy sajátértékének nevezzük.
Megjegyezzük a sajátértékek és a sajátvektorok néhány tulajdonságát.
1. Sajátvektorok tetszőleges lineáris kombinációja az azonos λ sajátértéknek megfelelő A operátor egy azonos sajátértékű sajátvektor.
2. Sajátvektorok A páronként eltérő λ 1 , λ 2 , …, λ m sajátértékekkel rendelkező A operátor lineárisan független.
3. Ha a λ 1 =λ 2 = λ m = λ sajátértékek, akkor a λ sajátérték legfeljebb m lineárisan független sajátvektornak felel meg.

Tehát, ha van n lineárisan független sajátvektor különböző λ 1 , λ 2 , …, λ n sajátértékeknek megfelelőek, akkor lineárisan függetlenek, ezért az R n tér alapjaként vehetők fel. Keressük meg az A lineáris operátor mátrixának alakját sajátvektorai alapján, amelyre az A operátorral a bázisvektorok alapján járunk el: Akkor .
Így az A lineáris operátor mátrixa a sajátvektorai alapján átlós alakú, és az A operátor sajátértékei az átlón vannak.
Van-e más alap, amelyben a mátrixnak átlós alakja van? Erre a kérdésre a következő tétel adja meg a választ.

Tétel. A bázisban lévő A lineáris operátor mátrixának (i ​​= 1..n) akkor és csak akkor van átlós alakja, ha a bázis összes vektora az A operátor sajátvektora.

Szabály sajátértékek és sajátvektorok megtalálására

Legyen a vektor , ahol x 1 , x 2 , …, x n - a vektor koordinátái a bázishoz viszonyítva és a λ sajátértéknek megfelelő A lineáris operátor sajátvektora, azaz. Ez a reláció mátrix alakban írható fel

. (*)

A (*) egyenlet egyenletnek tekinthető a , és a megtalálására, vagyis arra vagyunk kíváncsiak, nem triviális megoldások, mivel a sajátvektor nem lehet nulla. Ismeretes, hogy nem triviális megoldások homogén rendszer lineáris egyenletek akkor és csak akkor léteznek, ha det(A - λE) = 0. Így ahhoz, hogy λ az A operátor sajátértéke legyen, szükséges és elégséges, hogy det(A - λE) = 0.
Ha a (*) egyenletet részletesen koordináta alakban írjuk fel, akkor lineáris homogén egyenletrendszert kapunk:

(1)
Ahol a lineáris operátor mátrixa.

Az (1) rendszernek nullától eltérő megoldása van, ha D determinánsa nulla

Kaptunk egy egyenletet a sajátértékek meghatározására.
Ezt az egyenletet karakterisztikus egyenletnek, bal oldalát pedig az A mátrix (operátor) karakterisztikus polinomjának nevezzük. Ha a karakterisztikus polinomnak nincsenek valós gyökei, akkor az A mátrixnak nincsenek sajátvektorai, és nem redukálható átlós alakra.
Legyen λ 1 , λ 2 , …, λ n a karakterisztikus egyenlet valós gyökei, és lehetnek köztük többszörösek. Ezeket az értékeket behelyettesítve az (1) rendszerbe, megtaláljuk a sajátvektorokat.

12. példa. Az A lineáris operátor R 3-ban a törvény szerint működik, ahol x 1 , x 2 , .., x n a bázis vektorának koordinátái , , . Keresse meg ennek az operátornak a sajátértékeit és sajátvektorait.
Megoldás. Ennek az operátornak a mátrixát építjük fel:
.
Összeállítunk egy rendszert a sajátvektorok koordinátáinak meghatározására:

Összeállítjuk a karakterisztikus egyenletet és megoldjuk:

.
λ 1,2 = -1, λ 3 = 3.
Ha behelyettesítjük λ = -1-et a rendszerbe, a következőt kapjuk:
vagy
Mert , akkor van két függő változó és egy szabad változó.
Legyen x 1 tehát szabad ismeretlen Ezt a rendszert bármilyen módon megoldjuk, és megtaláljuk ennek a rendszernek az általános megoldását: A megoldások alapvető rendszere egy megoldásból áll, mivel n - r = 3 - 2 = 1.
A λ = -1 sajátértéknek megfelelő sajátvektorok halmazának alakja: , ahol x 1 bármely, nullától eltérő szám. Válasszunk egy vektort ebből a halmazból, például úgy, hogy x 1 = 1: .
Hasonlóan érvelve megtaláljuk a λ = 3 sajátértéknek megfelelő sajátvektort: .
Az R 3 térben a bázis három lineárisan független vektorból áll, de csak két lineárisan független sajátvektort kaptunk, amelyekből az R 3-ban lévő bázis nem képezhető. Következésképpen egy lineáris operátor A mátrixa nem redukálható átlós alakra.

13. példa Adott egy mátrix .
1. Bizonyítsuk be, hogy a vektor az A mátrix egy sajátvektora. Keresse meg az ennek a sajátvektornak megfelelő sajátértéket.
2. Keress egy bázist, amelyben az A mátrixnak átlós alakja van!
Megoldás.
1. Ha , akkor egy sajátvektor

.
Az (1, 8, -1) vektor egy sajátvektor. Sajátérték λ = -1.
A mátrixnak átlós alakja van a sajátvektorokból álló bázisban. Egyikük híres. Keressük a többit.
Sajátvektorokat keresünk a rendszerből:

Karakterisztikus egyenlet: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3, λ 2 = 1, λ 3 = -1.
Keresse meg a λ = -3 sajátértéknek megfelelő sajátvektort:

Ennek a rendszernek a mátrixának rangja egyenlő kettővel és egyenlő az ismeretlenek számával, ezért ennek a rendszernek csak nulla megoldása van x 1 = x 3 = 0. x 2 itt bármi más lehet, mint nulla, pl. x 2 = 1. Így a (0 ,1,0) vektor egy λ = -3-nak megfelelő sajátvektor. Ellenőrizzük:
.
Ha λ = 1, akkor megkapjuk a rendszert
A mátrix rangja kettő. Húzd át az utolsó egyenletet!
Legyen x 3 a szabad ismeretlen. Ezután x 1 \u003d -3x 3, 4x 2 = 10x 1 - 6x 3 \u003d -30x 3 - 6x 3, x 2 \u003d -9x 3.
Feltételezve, hogy x 3 = 1, van (-3,-9,1) - egy sajátvektorunk, amely megfelel a λ = 1 sajátértéknek. Ellenőrizzük:

.
Mivel a sajátértékek valósak és különbözőek, a hozzájuk tartozó vektorok lineárisan függetlenek, így R 3 -ban alapul vehetők. Így az alapban , , Az A mátrix alakja:
.
Az A:R n → R n lineáris operátor nem minden mátrixa redukálható átlós alakra, mivel egyes lineáris operátorok esetében kevesebb, mint n lineárisan független sajátvektor lehet. Ha azonban a mátrix szimmetrikus, akkor pontosan m lineárisan független vektor felel meg az m multiplicitás karakterisztikus egyenletének gyökerének.

Meghatározás. A szimmetrikus mátrix olyan négyzetmátrix, amelyben a főátlóhoz képest szimmetrikus elemek egyenlőek, vagyis amelyben .
Megjegyzések. 1. A szimmetrikus mátrix minden sajátértéke valós.
2. A páronként különböző sajátértékeknek megfelelő szimmetrikus mátrix sajátvektorai ortogonálisak.
A vizsgált apparátus számos alkalmazásának egyikeként a másodrendű görbe alakjának meghatározását tekintjük.

www.site lehetővé teszi, hogy megtalálja. Az oldal elvégzi a számítást. Néhány másodpercen belül a szerver megadja a helyes megoldást. A mátrix karakterisztikus egyenlete egy algebrai kifejezés lesz, amelyet a determináns kiszámításának szabálya talál mátrixok mátrixok, míg a főátlón eltérések lesznek az átlós elemek és a változó értékeiben. Számításkor karakterisztikus egyenlet az online mátrixhoz, minden elem mátrixok megszorozzuk a megfelelő egyéb elemekkel mátrixok. Keresés módban online csak négyzetre lehetséges mátrixok. Működés keresése karakterisztikus egyenlet az online mátrixhoz redukálódik az elemek szorzatának algebrai összegének kiszámítására mátrixok a determináns megtalálásának eredményeként mátrixok, csak annak megállapítása céljából karakterisztikus egyenlet az online mátrixhoz. Ez a művelet különleges helyet foglal el az elméletben mátrixok, lehetővé teszi sajátértékek és vektorok megtalálását a gyökök segítségével. Feladat keresése karakterisztikus egyenlet az online mátrixhoz az elemek szorzása mátrixok e termékek utólagos összegzésével egy bizonyos szabály szerint. www.site találja mátrix karakterisztikus egyenlete adott dimenzió a módban online. számítás karakterisztikus egyenlet az online mátrixhoz egy adott dimenziónál ez a determináns számítási szabálya által talált numerikus vagy szimbolikus együtthatós polinom megtalálása. mátrixok- a megfelelő elemek szorzatának összegeként mátrixok, csak annak megállapítása céljából karakterisztikus egyenlet az online mátrixhoz. Polinom keresése egy négyzet változójához mátrixok, mint meghatározás a mátrix karakterisztikus egyenlete, elméletben általános mátrixok. A polinom gyökeinek értéke karakterisztikus egyenlet az online mátrixhoz sajátvektorok és sajátértékek meghatározására szolgál mátrixok. Ha azonban a meghatározó mátrixok akkor nulla lesz mátrix karakterisztikus egyenlet továbbra is létezni fog, ellentétben a fordítottjával mátrixok. Számítás céljából mátrix karakterisztikus egyenlete vagy keressen egyszerre többet mátrixok karakterisztikus egyenletei, sok időt és erőfeszítést kell költenie, míg szerverünk megtalálja karakterisztikus egyenlet online mátrixhoz. Ebben az esetben a választ megtalálva karakterisztikus egyenlet az online mátrixhoz helyes és kellő pontosságú lesz, még akkor is, ha a számok megtalálásakor karakterisztikus egyenlet az online mátrixhoz irracionális lesz. Az oldalon www.site karakter bejegyzések megengedettek az elemekben mátrixok, vagyis karakterisztikus egyenlet online mátrixhoz számításnál általános szimbolikus formában ábrázolható karakterisztikus egyenletmátrix online. Hasznos ellenőrizni a kapott választ a megtalálási probléma megoldása során karakterisztikus egyenlet az online mátrixhoz az oldal használatával www.site. A polinom számítási műveletének végrehajtásakor - a mátrix karakterisztikus egyenlete, figyelmesnek és rendkívül koncentráltnak kell lenni a probléma megoldásában. Oldalunk viszont segít ellenőrizni a témával kapcsolatos döntését karakterisztikus egyenletmátrix online. Ha nincs ideje a megoldott problémák hosszú ellenőrzésére, akkor www.site minden bizonnyal kényelmes eszköz lesz a kereséshez és a számításhoz karakterisztikus egyenlet az online mátrixhoz.