Suprafața caselor este criteriul Fisher. Funcția Fisher în Excel și exemple ale activității sale

În acest exemplu, să considerăm cum este estimată fiabilitatea ecuației de regresie obținută. Același test este folosit pentru a testa ipoteza că coeficienții de regresie sunt ambii zero, a=0 , b=0 . Cu alte cuvinte, esența calculelor este de a răspunde la întrebarea: poate fi folosit pentru analize și prognoze ulterioare?

Utilizați acest test t pentru a determina asemănarea sau diferența dintre variațiile din două eșantioane.

Deci, scopul analizei este de a obține o estimare, cu ajutorul căreia s-ar putea afirma că, la un anumit nivel de α, ecuația de regresie rezultată este fiabilă statistic. Pentru aceasta se foloseşte coeficientul de determinare R2.
Semnificația modelului de regresie este verificată cu ajutorul testului F Fisher, a cărui valoare calculată se găsește ca raport dintre varianța seriei inițiale de observații a indicatorului studiat și estimarea nepărtinitoare a varianței secvenței reziduale pentru acest model.
Dacă valoarea calculată cu k 1 =(m) și k 2 =(n-m-1) grade de libertate este mai mare decât valoarea tabelară la un anumit nivel de semnificație, atunci modelul este considerat semnificativ.

unde m este numărul de factori din model.
Nota semnificație statistică baie de aburi regresie liniara produs conform următorului algoritm:
1. Se propune o ipoteză nulă conform căreia ecuația în ansamblu este nesemnificativă statistic: H 0: R 2 =0 la nivelul de semnificație α.
2. Apoi, determinați valoarea reală a criteriului F:


unde m=1 pentru regresia pe perechi.
3. Valoarea tabelului este determinată din tabelele de distribuție Fisher pentru un anumit nivel de semnificație, ținând cont de faptul că numărul de grade de libertate pentru suma totală a pătratelor (varianță mai mare) este 1 și numărul de grade de libertate pentru suma reziduală a pătrate (varianță mai mică) în regresia liniară este n-2 (sau via Funcția Excel FDISP(probabilitate,1,n-2)).
Tabelul F este valoarea maximă posibilă a criteriului sub influența unor factori aleatori pentru grade date de libertate și nivelul de semnificație α. Nivelul de semnificație α - probabilitatea de a respinge ipoteza corectă, cu condiția ca aceasta să fie adevărată. De obicei, α este considerat egal cu 0,05 sau 0,01.
4. Dacă valoarea reală a criteriului F este mai mică decât valoarea tabelului, atunci ei spun că nu există niciun motiv pentru a respinge ipoteza nulă.
În caz contrar, ipoteza nulă este respinsă și ipoteza alternativă despre semnificația statistică a ecuației în ansamblu este acceptată cu probabilitate (1-α).
Valoarea tabelului criteriului cu grade de libertate k 1 =1 și k 2 =48, F tabel = 4

concluzii: Deoarece valoarea reală a tabelului F > F, coeficientul de determinare este semnificativ statistic ( estimarea găsită a ecuației de regresie este fiabilă din punct de vedere statistic) .

Analiza variatiei

.

Indicatori de calitate ai ecuației de regresie

Exemplu. Pe baza unui total de 25 de întreprinderi comerciale, se studiază relația dintre semne: X - prețul mărfurilor A, mii de ruble; Y - profit întreprindere comercială, milioane de ruble La evaluarea modelului de regresie s-au obţinut următoarele rezultate intermediare: ∑(y i -y x) 2 = 46000; ∑(y i -y sr) 2 = 138000. Ce indicator de corelație poate fi determinat din aceste date? Calculați valoarea acestui indicator, pe baza acestui rezultat și folosind Testul F Fisher trageți o concluzie despre calitatea modelului de regresie.
Soluţie. Pe baza acestor date se poate determina o corelație empirică: , unde ∑(y cf -y x) 2 = ∑(y i -y cf) 2 - ∑(y i -y x) 2 = 138000 - 46000 = 92.000.
η 2 = 92000/138000 = 0,67, η = 0,816 (0,7< η < 0.9 - связь между X и Y высокая).

Testul F Fisher: n = 25, m = 1.
R 2 \u003d 1 - 46000 / 138000 \u003d 0,67, F \u003d 0,67 / (1-0,67)x (25 - 1 - 1) \u003d 46. F tabel (1; 23) \u003d 4.
Deoarece valoarea reală a lui F > Ftabl, estimarea găsită a ecuației de regresie este fiabilă din punct de vedere statistic.

Întrebare: Ce statistică este folosită pentru a testa semnificația unui model de regresie?
Răspuns: Pentru semnificația întregului model în ansamblu, sunt utilizate statisticile F (criteriul lui Fisher).

Funcția FISHER returnează transformarea Fisher a argumentelor X . Această transformare construiește o funcție care are o distribuție normală mai degrabă decât asimetrică. Funcția FISHER este utilizată pentru a testa ipoteza folosind coeficientul de corelație.

Descrierea funcției FISHER în Excel

Când lucrați cu această funcție, trebuie să setați valoarea variabilei. Trebuie remarcat imediat că există unele situații în care această funcție nu va produce rezultate. Acest lucru este posibil dacă variabila:

• nu este un număr. Într-o astfel de situație, funcția FISHER va returna valoarea de eroare #VALOARE!;
• este fie mai mică decât -1, fie mai mare decât 1. În acest caz, funcția FISHER va returna valoarea de eroare #NUM!.

Ecuația care este folosită pentru a descrie matematic funcția FISHER este:

Z"=1/2*ln(1+x)/(1-x)

Să luăm în considerare aplicarea acestei funcții pe 3 exemple specifice.



Evaluarea relației dintre profit și costuri folosind funcția FISHER

Exemplul 1. Folosind datele despre activitatea organizațiilor comerciale, se cere să se facă o evaluare a relației dintre profitul Y (milioane de ruble) și costurile X (milioane de ruble) utilizate pentru dezvoltarea produselor (date în tabelul 1).

Tabelul 1 - Date inițiale:

№	X	Y
1	210.000.000,00 RUB	95.000.000,00 USD
2	1.068.000.000,00 RUB	76.000.000,00 RUB
3	1.005.000.000,00 RUB	78.000.000,00 RUB
4	610.000.000,00 RUB	89.000.000,00 RUB
5	768.000.000,00 RUB	77.000.000,00 RUB
6	799.000.000,00 RUB	85.000.000,00 RUB

Schema de rezolvare a unor astfel de probleme este următoarea:

1. Calculat coeficient liniar corelații r xy ;
2. Semnificația coeficientului de corelație liniară este verificată pe baza testului t Student. În același timp, este înaintată și testată ipoteza despre egalitatea coeficientului de corelație cu zero. La testarea acestei ipoteze, se utilizează statistica t. Dacă ipoteza este confirmată, statistica t are o distribuție Student. Dacă valoarea calculată t p > t cr, atunci se respinge ipoteza, ceea ce indică semnificația coeficientului de corelație liniară și, în consecință, semnificația statistică a relației dintre X și Y;
3. Se determină o estimare de interval pentru un coeficient de corelație liniară semnificativ statistic.
4. O estimare a intervalului pentru coeficientul de corelație liniară este determinată pe baza z-transforma inversă Pescar;
5. Se calculează eroarea standard a coeficientului de corelație liniară.

Rezultatele rezolvării acestei probleme cu funcțiile utilizate în pachetul Excel sunt prezentate în Figura 1.

Figura 1 - Un exemplu de calcule.

Nu. p / p	Numele indicatorului	Formula de calcul
1	Coeficient de corelație	=CORREL(B2:B7;C2:C7)
2	Valoarea estimată a criteriului t tp	=ABS(C8)/ROOT(1-PUTERE(C8,2))*ROOT(6-2)
3	Valoarea tabelului t-test trh	=STUDISP(0,05,4)
4	Valoarea de tabel a standardului distributie normala zy	=NORMINV((0,95+1)/2)
5	Valoarea transformării Fischer z'	=FISHER(C8)
6	Estimarea intervalului stâng pentru z	=C12-C11*ROOT(1/(6-3))
7	Estimarea intervalului drept pentru z	=C12+C11*ROOT(1/(6-3))
8	Estimarea intervalului stâng pentru rxy	=FISCHEROBR(C13)
9	Estimarea intervalului corect pentru rxy	=FISCHEROBR(C14)
10	Abaterea standard pentru rxy	=ROOT((1-C8^2)/4)

Astfel, cu o probabilitate de 0,95, coeficientul de corelație liniară se află în intervalul de la (–0,386) la (–0,990) cu eroare standard 0,205.

Verificarea semnificației statistice a regresiei asupra funcției FDISP

Exemplul 2. Verificați semnificația statistică a ecuației regresie multiplă folosind testul F al lui Fisher, trageți concluzii.

Pentru a testa semnificația ecuației în ansamblu, propunem ipoteza H 0 despre nesemnificația statistică a coeficientului de determinare și ipoteza opusă H 1 despre semnificația statistică a coeficientului de determinare:

H1: R2≠ 0.

Să testăm ipotezele folosind testul F al lui Fisher. Indicatorii sunt prezentați în tabelul 2.

Tabelul 2 - Date inițiale

Pentru a face acest lucru, folosim următoarea funcție din pachetul Excel:

FDISP(α;p;n-p-1)

• α este probabilitatea asociată cu distribuția dată;
• p și n sunt numărătorul și, respectiv, numitorul gradelor de libertate.

Știind că α = 0,05, p = 2 și n = 53, obținem următoarea valoare pentru F crit (vezi Figura 2).

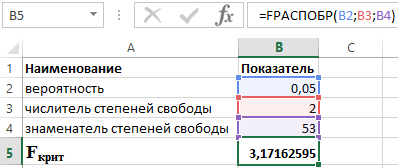
Figura 2 - Un exemplu de calcule.

Astfel, putem spune că F calc > F crit. Ca urmare, este acceptată ipoteza H 1 despre semnificația statistică a coeficientului de determinare.

Calculul valorii indicatorului de corelare în Excel

Exemplul 3. Folosind datele a 23 de întreprinderi despre: X - prețul produsului A, mii de ruble; Y - profitul unei întreprinderi comerciale, milioane de ruble, dependența lor este studiată. Evaluarea modelului de regresie a dat următoarele: ∑(yi-yx) 2 = 50000; ∑(yi-yср) 2 = 130000. Ce indicator de corelație poate fi determinat din aceste date? Calculați valoarea indicelui de corelație și, folosind testul Fisher, trageți o concluzie despre calitatea modelului de regresie.

Să definim F crit din expresia:

F calc \u003d R 2 / 23 * (1-R 2)

unde R este coeficientul de determinare egal cu 0,67.

Astfel, valoarea calculată F calc = 46.

Pentru a determina F crit, folosim distribuția Fisher (vezi Figura 3).

Figura 3 - Un exemplu de calcule.

Astfel, estimarea obținută a ecuației de regresie este fiabilă.

criteriul lui Fisher

Criteriul lui Fisher este utilizat pentru a testa ipoteza despre egalitatea varianțelor a două populații generale distribuite conform legii normale. Este un criteriu parametric.

Testul F al lui Fisher se numește raportul de varianță, deoarece este format ca raport a două estimări imparțiale comparate ale variațiilor.

Să se obțină două mostre ca rezultat al observațiilor. Pe baza acestora, variațiile și având Și grade de libertate. Vom presupune că primul eșantion este luat din populația generală cu o varianță , iar al doilea - din populația generală cu o varianță . Este prezentată ipoteza nulă cu privire la egalitatea celor două varianțe, i.e. H0:
sau . Pentru a respinge această ipoteză, este necesar să se dovedească semnificația diferenței la un anumit nivel de semnificație.
.

Valoarea criteriului se calculează prin formula:

Evident, dacă varianțele sunt egale, valoarea criteriului va fi egală cu unu. În alte cazuri, va fi mai mare (mai puțin) decât unu.

Criteriul are o distribuție Fisher
. Testul lui Fisher este un test cu două cozi și ipoteza nulă
respins în favoarea alternativei
Dacă . Aici unde
sunt volumele primei și, respectiv, celei de-a doua probe.

Sistemul STATISTICA implementează un test Fisher cu o singură coadă, de ex. ca întotdeauna luați dispersia maximă. În acest caz, ipoteza nulă este respinsă în favoarea alternativei dacă .

Exemplu

Lăsați sarcina să fie setată pentru a compara eficiența formării a două grupuri de studenți. Nivelul de progres caracterizează nivelul de management al procesului de învăţare, iar dispersia caracterizează calitatea managementului învăţării, gradul de organizare a procesului de învăţare. Ambii indicatori sunt independenți și caz general ar trebui luate în considerare în comun. Nivelul de progres (așteptările matematice) al fiecărui grup de elevi este caracterizat de media aritmetică și , iar calitatea este caracterizată de variațiile eșantionului corespunzătoare ale estimărilor: și . La evaluarea nivelului de performanță actuală, s-a dovedit că este același pentru ambii studenți: == 4,0. Variante de eșantion:
Și
. Numărul de grade de libertate corespunzător acestor estimări:
Și
. Prin urmare, pentru a stabili diferențe în eficacitatea pregătirii, putem folosi stabilitatea performanței academice, i.e. să testăm ipoteza.

Calcula
(numărătorul ar trebui să aibă o variație mare), . Conform tabelelor ( STATISTICI – Probabilitatedistributiecalculator) găsim , care este mai puțin decât calculat, prin urmare, ipoteza nulă trebuie respinsă în favoarea alternativei . Este posibil ca această concluzie să nu satisfacă cercetătorul, deoarece este interesat de adevărata valoare a raportului
(avem întotdeauna o variație mare în numărător). Când verificăm un criteriu unilateral, obținem , care este mai mic decât valoarea calculată mai sus. Deci, ipoteza nulă trebuie respinsă în favoarea alternativei.

Testul lui Fisher în programul STATISTICA în mediul Windows

Pentru un exemplu de testare a unei ipoteze (criteriul lui Fisher), folosim (creăm) un fișier cu două variabile (fisher.sta):

Orez. 1. Tabel cu două variabile independente

Pentru a testa ipoteza, este necesar în statistica de bază ( De bazăStatisticișiMese) alegeți testul Student pentru variabile independente. ( t-test, independent, prin variabile).

Orez. 2. Testarea ipotezelor parametrice

După selectarea variabilelor și apăsarea tastei rezumat se calculează valorile abaterilor standard și testul Fisher. În plus, se determină nivelul de semnificație p, unde diferența este nesemnificativă.

Orez. 3. Rezultatele testării ipotezei (testul F)

Folosind Probabilitatecalculator iar prin setarea valorii parametrilor, puteți reprezenta un grafic distribuția Fisher cu un semn al valorii calculate.

Orez. 4. Zona de acceptare (respingere) a ipotezei (criteriul F)

Surse.

Testarea ipotezelor despre relația dintre două varianțe

URL: /tryphonov3/terms3/testdi.htm

Cursul 6. :8080/resources/math/mop/lections/lection_6.htm

F - criteriul Fisher

URL: /home/portal/applications/Multivariatadvisor/F-Fisheer/F-Fisheer.htm

Teoria și practica cercetării probabilistice și statistice.

Adresa URL: /active/referats/read/doc-3663-1.html

F - criteriul Fisher

criteriul lui Fisher vă permite să comparați valorile variațiilor eșantionului a două eșantioane independente. Pentru a calcula F emp, trebuie să găsiți raportul dintre variațiile a două eșantioane și astfel încât varianța mai mare să fie în numărător, iar cea mai mică să fie în numitor. Formula de calcul a criteriului Fisher este următoarea:

unde sunt variațiile primului și, respectiv, celui de-al doilea eșantion.

Întrucât, în funcție de condiția criteriului, valoarea numărătorului trebuie să fie mai mare sau egală cu valoarea numitorului, valoarea lui Femp va fi întotdeauna mai mare sau egală cu unu.

Numărul de grade de libertate este, de asemenea, definit simplu:

k 1 =n l - 1 pentru primul eșantion (adică pentru eșantionul a cărui varianță este mai mare) și k 2 = n 2 - 1 pentru a doua probă.

În Anexa 1, valorile critice ale criteriului Fisher sunt găsite prin valorile k 1 (linia de sus a tabelului) și k 2 (coloana din stânga a tabelului).

Dacă t emp >t crit, atunci se acceptă ipoteza nulă, în caz contrar se acceptă alternativa.

Exemplul 3 Testarea a fost efectuată în două clase a treia dezvoltare mentală conform testului TURMSh a zece elevi. Valorile medii obținute nu au diferit semnificativ, cu toate acestea, psihologul este interesat de întrebare - există diferențe în gradul de omogenitate a indicatorilor de dezvoltare mentală între clase.

Soluţie. Pentru criteriul Fisher, este necesar să se compare variațiile scorurilor la test în ambele clase. Rezultatele testelor sunt prezentate în tabel:

Tabelul 3

Nr de elevi	Clasa întâi	Clasa a doua

După ce am calculat varianțele pentru variabilele X și Y, obținem:

s X 2 = 572,83; s y 2 =174,04

Apoi, conform formulei (8) pentru calculul conform criteriului F Fisher, găsim:

Conform tabelului din Anexa 1 pentru criteriul F cu grade de libertate în ambele cazuri egale cu k=10 - 1 = 9 găsim F crit = 3,18 (<3.29), следовательно, в терминах статистических гипотез можно утвер­ждать, что Н 0 (гипотеза о сходстве) может быть отвергнута на уровне 5%, а принимается в этом случае гипотеза Н 1 . Иcследователь может утверждать, что по степени однородности такого показа­теля, как умственное развитие, имеется различие между выбор­ками из двух классов.

6.2 Teste neparametrice

Comparând cu ochi (în procente) rezultatele înainte și după orice expunere, cercetătorul ajunge la concluzia că dacă se observă diferențe, atunci există o diferență în probele comparate. O astfel de abordare este categoric inacceptabilă, deoarece este imposibil să se determine nivelul de încredere în diferențele pentru procente. Procentele luate de sine stătătoare nu permit tragerea unor concluzii sigure din punct de vedere statistic. Pentru a demonstra eficacitatea oricărui impact, este necesar să se identifice o tendință semnificativă statistic în schimbarea (deplasarea) indicatorilor. Pentru a rezolva astfel de probleme, cercetătorul poate folosi o serie de criterii de diferență. Mai jos vor fi luate în considerare teste neparametrice: testul semnului și testul chi-pătrat.

)

Calculul criteriului φ*

1. Determinați acele valori ale atributului care vor constitui criteriul de împărțire a subiecților în cei care „au efect” și cei care „nu au efect”. Dacă trăsătura este cuantificată, utilizați criteriul λ pentru a găsi punctul optim de împărțire.

2. Desenați un tabel cu patru celule (sinonim: patru câmpuri) de două coloane și două rânduri. Prima coloană este „există un efect”; a doua coloană este „fără efect”; prima linie din partea de sus - 1 grup (probă); a doua linie - 2 grup (probă).

4. Numărați numărul de subiecți din primul eșantion care au „niciun efect” și introduceți acest număr în celula din dreapta sus a tabelului. Calculați suma primelor două celule. Ar trebui să se potrivească cu numărul de subiecți din primul grup.

6. Numărați numărul de subiecți din cel de-al doilea eșantion care au „niciun efect” și introduceți acest număr în celula din dreapta jos a tabelului. Calculați suma celor două celule de jos. Ar trebui să se potrivească cu numărul de subiecți din al doilea grup (eșantion).

7. Determinați procentul subiecților care „au efect” raportând numărul lor la numărul total de subiecți din acest grup (eșantion). Înregistrați procentele rezultate în celulele din stânga sus și, respectiv, din stânga jos ale tabelului, între paranteze, pentru a nu le confunda cu valorile absolute.

8. Verificați dacă unul dintre procentele potrivite este egal cu zero. Dacă acesta este cazul, încercați să schimbați acest lucru mutând punctul de împărțire al grupurilor într-o parte sau cealaltă. Dacă acest lucru este imposibil sau nedorit, eliminați criteriul φ* și utilizați criteriul χ2.

9. Determinați conform tabelului. XII Anexa 1 valorile unghiurilor φ pentru fiecare dintre procentele comparate.

unde: φ1 - unghiul corespunzător procentului mai mare;

φ2 - unghi corespunzător unui procent mai mic;

N1 - numărul de observații din eșantionul 1;

N2 - numărul de observații din eșantionul 2.

11. Comparați valoarea obținută φ* cu valorile critice: φ* ≤1,64 (р<0,05) и φ* ≤2,31 (р<0,01).

Dacă φ*emp ≤φ*cr. H0 este respins.

Dacă este necesar, determinați nivelul exact de semnificație al φ*emp obținut conform tabelului. XIII Anexa 1.

Această metodă este descrisă în multe manuale (Plokhinsky N.A., 1970; Gubler E.V., 1978; Ivanter E.V., Korosov A.V., 1992, etc.) Această descriere se bazează pe versiunea metodei care a fost dezvoltată și prezentată de E.V. Gubler.

Scopul criteriului φ*

Testul lui Fisher este conceput pentru a compara două eșantioane în funcție de frecvența de apariție a efectului (indicatorului) de interes pentru cercetător. Cu cât este mai mare, cu atât diferențele sunt mai fiabile.

Descrierea criteriului

Criteriul evaluează fiabilitatea diferențelor dintre acele procente din două eșantioane în care se înregistrează efectul (indicatorul) care ne interesează. Figurat vorbind, comparăm cele mai bune 2 bucăți tăiate din 2 plăcinte între ele și decidem care dintre ele este cu adevărat mai mare.

Esența transformării unghiulare Fisher este conversia procentelor în unghiuri centrale, care sunt măsurate în radiani. Un procent mai mare va corespunde unui unghi mai mare φ, iar un procent mai mic va corespunde unui unghi mai mic, dar relațiile aici nu sunt liniare:

unde P este un procent exprimat în fracții de unitate (vezi Fig. 5.1).

Cu discrepanța crescândă între unghiurile φ 1 și φ 2 iar o creștere a numărului de probe, valoarea criteriului crește. Cu cât valoarea φ* este mai mare, cu atât este mai probabil ca diferențele să fie semnificative.

Ipoteze

H 0 : Ponderea persoanelor, care manifestă efectul studiat, în eșantionul 1 nu mai mult decât în ​​eșantionul 2.

H 1 : Proporția persoanelor care arată efectul studiat este mai mare în eșantionul 1 decât în ​​eșantionul 2.

Reprezentarea grafică a unui criteriu φ*

Metoda transformării unghiulare este oarecum mai abstractă decât restul criteriilor.

Formula la care aderă E. V. Gubler la calcularea valorilor lui φ presupune că 100% este unghiul φ=3,142, adică valoarea rotunjită π=3,14159... Acest lucru ne permite să reprezentăm mostrele comparate sub formă de două semicercuri, fiecare dintre ele simbolizează 100% din numărul eșantionului lor. Procentele subiecților cu „efect” vor fi prezentate ca sectoare formate din unghiurile centrale φ. Pe Fig. Figura 5.2 prezintă două semicercuri ilustrând Exemplul 1. În primul eșantion, 60% dintre subiecți au rezolvat problema. Acest procent corespunde unghiului φ=1,772. În al doilea eșantion, 40% dintre subiecți au rezolvat problema. Acest procent corespunde unghiului φ =1,369.

Criteriul φ* face posibilă determinarea dacă unul dintre unghiuri este statistic semnificativ superior celuilalt pentru dimensiunile eșantionului date.

Restricții de criterii φ*

1. Niciuna dintre acțiunile comparate nu trebuie să fie egală cu zero. Formal, nu există obstacole în calea aplicării metodei φ în cazurile în care proporția de observații dintr-unul dintre eșantioane este 0. Cu toate acestea, în aceste cazuri, rezultatul poate fi nerezonabil de mare (Gubler E.V., 1978, p. 86) .

2. Sus nu există o limită în criteriul φ - eșantioanele pot fi arbitrar mari.

Inferior limita este de 2 observații într-unul dintre eșantioane. Cu toate acestea, trebuie respectate următoarele rapoarte în dimensiunea celor două eșantioane:

a) dacă există doar 2 observații într-o probă, atunci a doua trebuie să aibă cel puțin 30:

b) dacă una dintre probe are doar 3 observații, atunci a doua trebuie să aibă cel puțin 7:

c) dacă una dintre probe are doar 4 observații, atunci a doua trebuie să aibă cel puțin 5:

d) lan 1 , n 2 ≥ 5 orice comparatie este posibila.

În principiu, este posibil să se compare și eșantioane care nu îndeplinesc această condiție, de exemplu, cu relațian 1 =2, n 2 = 15, dar în aceste cazuri nu se vor putea detecta diferențe semnificative.

Criteriul φ* nu are alte restricții.

Să ne uităm la câteva exemple pentru a ilustra posibilitățilecriteriul φ*.

Exemplul 1: compararea probelor în funcție de o caracteristică determinată calitativ.

Exemplul 2: compararea probelor în funcție de un atribut măsurat cantitativ.

Exemplul 3: compararea eșantioanelor atât în ​​ceea ce privește nivelul cât și distribuția unei caracteristici.

Exemplul 4: utilizarea criteriului φ* în combinație cu criteriulX Kolmogorov-Smirnov pentru a obține cel mai precis rezultat.

Exemplul 1 - compararea probelor după o caracteristică determinată calitativ

În această utilizare a testului, comparăm procentul de subiecți dintr-un eșantion care sunt caracterizați de o anumită calitate cu procentul de subiecți dintr-un alt eșantion care sunt caracterizați de aceeași calitate.

Să presupunem că ne interesează dacă două grupuri de elevi diferă în ceea ce privește succesul lor în rezolvarea unei noi probleme experimentale. În primul grup de 20 de persoane, 12 persoane i-au făcut față, iar în al doilea eșantion de 25 de persoane - 10. În primul caz, procentul celor care au rezolvat problema va fi de 12/20 100% = 60% și în al doilea 10/25 100% = 40%. Aceste procente diferă semnificativ cu datele?n 1 Șin 2 ?

S-ar părea că „prin ochi” se poate determina că 60% este mult mai mare decât 40%. Cu toate acestea, aceste diferențe sunt de faptn 1 , n 2 nesigure.

Hai să verificăm. Deoarece ne interesează faptul de a rezolva problema, vom considera succesul în rezolvarea problemei experimentale ca un „efect”, iar eșecul în rezolvarea acesteia ca absența unui efect.

Să formulăm ipoteze.

H 0 : Ponderea persoanelora făcut față sarcinii, în primul grup nu mai mult decât în ​​al doilea grup.

H 1 : Proporția persoanelor care au făcut față sarcinii în primul grup este mai mare decât în ​​al doilea grup.

Acum să construim așa-numitul tabel cu patru celule sau patru câmpuri, care este de fapt un tabel de frecvențe empirice pentru două valori de atribut: „există un efect” - „nu există niciun efect”.

Tabelul 5.1

Un tabel cu patru celule pentru calcularea criteriului atunci când se compară două grupuri de subiecți în funcție de procentul celor care au rezolvat problema.

Grupuri	„Există un efect”: sarcina este rezolvată			„Fără efect”: problema nu este rezolvată			Sume
	Cantitate subiecții de testare	% acțiune		Cantitate subiecții de testare	% acțiune
1 grup		(60%)			(40%)
2 grupa		(40%)			(60%)
Sume

Într-un tabel cu patru celule, de regulă, coloanele „Există un efect” și „Fără efect” sunt marcate deasupra, iar rândurile „Grup 1” și „Grup 2” sunt în stânga. De fapt, doar câmpurile (celulele) A și B participă la comparații, adică procentele din coloana „Există un efect”.

Conform Tabelului.XIIAnexa 1 definește valorile lui φ corespunzătoare procentelor din fiecare dintre grupuri.

Acum să calculăm valoarea empirică a lui φ* folosind formula:

unde φ 1 - unghiul corespunzător cotei % mai mari;

φ 2 - unghiul corespunzător cotei % mai mici;

n 1 - numărul de observații din eșantionul 1;

n 2 - numărul de observații din eșantion 2.

În acest caz:

Conform Tabelului.XIIIAnexa 1 determină ce nivel de semnificație corespunde lui φ* emp=1,34:

p=0,09

De asemenea, se pot stabili valori critice ale φ* corespunzătoare nivelurilor de semnificație statistică acceptate în psihologie:

Să construim o „axă a semnificației”.

Valoarea empirică φ* obținută se află în zona de nesemnificație.

Răspuns: H 0 admis. Proporția de oameni care au finalizat sarcinaVprimul grup nu mai mult decât al doilea grup.

Nu se poate simpatiza decât cu un cercetător care consideră diferențe semnificative de 20% și chiar 10% fără a le verifica fiabilitatea folosind criteriul φ*. În acest caz, de exemplu, doar diferențe de cel puțin 24,3% ar fi semnificative.

Se pare că atunci când comparăm două eșantioane după un criteriu calitativ, criteriul φ ne poate supăra mai degrabă decât să ne mulțumească. Ceea ce părea semnificativ, din punct de vedere statistic, poate să nu fie așa.

Mult mai multe oportunități de a-i face pe plac cercetătorului apar cu criteriul Fisher atunci când comparăm două mostre în funcție de trăsături măsurate cantitativ și putem varia „efectul.

Exemplul 2 - compararea a două probe în funcție de un atribut măsurat cantitativ

În această variantă de utilizare a criteriului, comparăm procentul subiecților dintr-un eșantion care ating un anumit nivel al unei valori caracteristice cu procentul subiecților care ating acest nivel într-un alt eșantion.

Într-un studiu al lui G. A. Tlegenova (1990), din 70 de tineri care studiază la școli profesionale cu vârsta cuprinsă între 14 și 16 ani, au fost selectați 10 subiecți cu un scor mare pe scara de agresivitate și 11 subiecți cu un scor scăzut pe scala de agresivitate. rezultatele unui sondaj folosind Chestionarul de personalitate Freiburg. Este necesar să se stabilească dacă grupurile de tineri agresivi și neagresivi diferă în ceea ce privește distanța pe care o aleg spontan într-o conversație cu un coleg. Datele lui G. A. Tlegenova sunt prezentate în tabel. 5.2. Se poate observa că tinerii agresivi aleg mai des o distanță de 50cm sau chiar mai puțin, în timp ce tinerii neagresivi sunt mai predispuși să aleagă distanțe mai mari de 50 cm.

Acum putem considera o distanță de 50 cm drept critică și considerăm că dacă distanța aleasă de subiect este mai mică sau egală cu 50 cm, atunci există un „efect”, iar dacă distanța aleasă este mai mare de 50 cm, atunci nu are efect. Observăm că la lotul tinerilor agresivi, efectul se observă în 7 din 10, adică în 70% din cazuri, iar la lotul tinerilor neagresivi, în 2 din 11, adică în 18,2. % din cazuri. Aceste procente pot fi comparate folosind metoda φ* pentru a stabili validitatea diferențelor dintre ele.

Tabelul 5.2

Indicatori ai distanței (în cm) alese de tinerii agresivi și neagresivi într-o conversație cu un coleg (conform lui G.A. Tlegenova, 1990)

	Grupa 1: băieți cu scoruri mari la scala de AgresivitateFPI- R (n 1 =10)		Grupa 2: băieți cu scoruri scăzute la scala de agresivitateFPI- R (n 2 =11)
	DC m )	% acțiune	DC M )	% acțiune
"Mânca Efect" d≤50 cm
				18,2%
"Nu efect" d>50 cm
	80 QO			81,8%
Sume		100%		100%
Mediu	5b:o		77.3

Să formulăm ipoteze.

H 0 d ≤ 50 vezi, nu există băieți mai agresivi în grup decât în ​​grupul băieților neagresivi.

H 1 : Proporția de oameni care aleg o distanțăd≤ 50 cm, în lotul băieților agresivi mai mult decât în ​​grupul băieților neagresivi. Acum să construim așa-numitul tabel cu patru celule.

Tabelul 53

Un tabel cu patru celule pentru calcularea criteriului φ* atunci când se compară grupuri de agresivi (nf=10) și băieți neagresivi (n2=11)

Grupuri	„Există un efect”: d≤50			"Fara efect." d>50			Sume
	Numărul de subiecți de testare	(% acțiune)		Numărul de subiecți de testare	(% acțiune)
Grupa 1 - băieți agresivi		(70%)			(30%)
Grupa 2 - băieți neagresivi		(180%)			(81,8%)
Sumă

Conform Tabelului.XIIAnexa 1 definește valorile lui φ corespunzătoare procentului „efectului” în fiecare dintre grupuri.

Valoarea empirică obținută φ* se află în zona de semnificație.

Răspuns: H 0 respins. admisH 1 . Proporția persoanelor care aleg o distanță într-o conversație mai mică sau egală cu 50 cm este mai mare în grupul băieților agresivi decât în ​​grupul băieților neagresivi

Pe baza rezultatului obținut, putem concluziona că băieții mai agresivi aleg mai des o distanță mai mică de jumătate de metru, în timp ce băieții neagresivi aleg mai des o distanță mai mare de jumătate de metru. Vedem că tinerii agresivi comunică de fapt la granița zonelor intime (0-46 cm) și personale (de la 46 cm). Ne amintim, totuși, că distanța intimă între parteneri este apanajul nu numai a unor bune relații apropiate, ciȘilupta corp la corp (SalaE. T., 1959).

Exemplul 3 - compararea mostrelor atât în ​​ceea ce privește nivelul cât și distribuția unei caracteristici.

În această variantă de utilizare a testului, putem verifica mai întâi dacă grupurile diferă în ceea ce privește nivelul oricărei trăsături, apoi comparăm distribuțiile trăsăturii în două eșantioane. O astfel de sarcină poate fi relevantă în analiza diferențelor dintre intervalele sau forma de distribuție a estimărilor obținute de subiecți folosind o metodă nouă.

În studiul lui R. T. Chirkina (1995), a fost folosit pentru prima dată un chestionar, care urmărea identificarea unei tendințe de scoatere din memorie a faptelor, numelor, intențiilor și metodelor de acțiune, din cauza complexelor personale, familiale și profesionale. Chestionarul a fost creat cu participarea lui E. V. Sidorenko pe baza materialelor cărții 3. Freud „Psihopatologia vieții de zi cu zi”. Un eșantion de 50 de studenți ai Institutului Pedagogic, necăsătoriți, fără copii, cu vârsta cuprinsă între 17 și 20 de ani, a fost examinat folosind acest chestionar, precum și tehnica Menester-Corzini pentru a identifica intensitatea sentimentului de insuficiență proprie,sau"complex de inferioritate"ManasterG. J., CorsiniR. J., 1982).

Rezultatele sondajului sunt prezentate în tabel. 5.4.

Se poate susține că există relații semnificative între indicatorul energiei deplasării, diagnosticat cu ajutorul chestionarului, și indicatorii de intensitate, sentimentul propriei insuficiențe?

Tabelul 5.4

Indicatori ai intensității sentimentului de insuficiență proprie în grupuri de elevi cu (nj=18) și energie de deplasare scăzută (n2=24).

Grupa 1: energie de deplasare de la 19 la 31 de puncte (n 1 =181		Grupa 2: energie de deplasare de la 7 la 13 puncte (n 2 =24)
0; 0; 0; 0; 0 20; 20 30; 30; 30; 30; 30; 30; 30 50; 50 60; 60		0; 0 5; 5; 5; 5 10; 10; 10; 10; 10; 10 15; 15 20; 20; 20; 20 30; 30; 30; 30; 30; 30
Sume Mediu	26,11	15,42

În ciuda faptului că valoarea medie în grupul cu deplasare mai viguroasă este mai mare, în acesta se observă și 5 valori zero. Dacă comparăm histogramele distribuției estimărilor în două eșantioane, atunci se găsește un contrast izbitor între ele (Fig. 5.3).

Pentru a compara două distribuții, am putea aplica criteriulχ 2 sau criteriuλ , dar pentru aceasta ar trebui să mărim cifrele, și în plus, în ambele mostren <30.

Criteriul φ* ne va permite să verificăm efectul discrepanței dintre cele două distribuții observate pe grafic, dacă suntem de acord să considerăm că există un „efect” dacă indicatorul sentimentului de insuficiență ia fie foarte scăzut (0) sau, dimpotrivă, valori foarte mari (S30) și că nu există „niciun efect” dacă scorul de lipsă este în intervalul mediu, între 5 și 25.

Să formulăm ipoteze.

H 0 : Valorile extreme ale indicelui de insuficiență (fie 0, fie 30 sau mai mult) în grupul cu represiune mai viguroasă nu sunt mai frecvente decât în ​​grupul cu represiune mai puțin viguroasă.

H 1 : Valorile extreme ale indicelui de insuficiență (fie 0, fie 30 sau mai mult) în grupul cu represiune mai viguroasă sunt mai frecvente decât în ​​grupul cu represiune mai puțin viguroasă.

Să creăm un tabel cu patru celule, convenabil pentru calcularea suplimentară a criteriului φ*.

Tabelul 5.5

Tabel cu patru celule pentru calcularea criteriului φ* la compararea grupurilor cu energie de deplasare mai mare și mai mică în funcție de raportul indicatorilor de insuficiență

Grupuri	„Este eficient”: scorul deficienței este 0 sau >30		„Fără efect”: scor de deficiență de la 5 la 25		Sume
		(88,9%)		(11,1%)
		(33,3%)		(66,7%)
Sume

Conform Tabelului.XIIAnexa 1, definim valorile lui φ corespunzătoare procentelor comparate:

Să calculăm valoarea empirică a lui φ*:

Valori critice ale φ* pentru oricaren 1 , n 2 , după cum ne amintim din exemplul anterior, sunt:

Tab.XIIIAnexa 1 ne permite să determinăm mai precis nivelul de semnificație al rezultatului obținut: p<0,001.

Răspuns: H 0 respins. admisH 1 . Valorile extreme ale indicelui de insuficiență (fie 0, fie 30 sau mai mult) în grupul cu o energie de deplasare mai mare sunt mai frecvente decât în ​​grupul cu o energie de deplasare mai mică.

Deci, subiecții cu energie de represiune mai mare pot avea atât indicatori foarte mari (30 sau mai mult) cât și foarte scăzuti (zero) de a-și simți propria insuficiență. Se poate presupune că își reprimă atât nemulțumirea, cât și nevoia de succes în viață. Aceste ipoteze necesită o verificare suplimentară.

Rezultatul obținut, indiferent de interpretarea sa, confirmă posibilitatea criteriului φ* în evaluarea diferențelor în forma distribuției trăsăturilor în două eșantioane.

Au fost 50 de persoane în eșantionul inițial, dar 8 dintre aceștia au fost excluși din luarea în considerare ca având un scor mediu la indicatorul anergiei deplasării (14-15). Indicatorii intensității sentimentului de insuficiență sunt, de asemenea, medii: 6 valori de 20 de puncte și 2 valori de 25 de puncte.

Posibilitățile puternice ale criteriului φ* pot fi văzute confirmând o ipoteză complet diferită atunci când se analizează materialele acestui exemplu. Putem demonstra, de exemplu, că într-un grup cu o energie de represiune mai mare, indicatorul de deficiență este tot mai mare, în ciuda caracterului paradoxal al distribuției sale în acest grup.

Să formulăm noi ipoteze.

H 0 Cele mai mari valori ale indicelui de insuficiență (30 sau mai mult) în grupul cu o energie de deplasare mai mare se găsesc nu mai des decât în ​​grupul cu o energie de deplasare mai mică.

H 1 : Cele mai mari valori ale indicelui de insuficiență (30 sau mai mult) în grupul cu o energie de deplasare mai mare sunt mai frecvente decât în ​​grupul cu o energie de deplasare mai mică. Să construim un tabel cu patru câmpuri folosind datele din Tabel. 5.4.

Tabelul 5.6

Tabel cu patru celule pentru calcularea criteriului φ* la compararea grupurilor cu energie de deplasare mai mare și mai mică în funcție de nivelul indicelui de deficiență

Grupuri	„Există un efect”* indicatorul de deficiență este mai mare sau egal cu 30		„Fără efect”: Scorul de deficiență este mai mic 30		Sume
Grupa 1 - cu energie de deplasare mai mare		(61,1%)		(38.9%)
Grupa 2 - cu energie de deplasare mai mică		(25.0%)		(75.0%)
Sume

Conform Tabelului.XIIIAnexa 1 determină că acest rezultat corespunde unui nivel de semnificație de p=0,008.

Răspuns: Dar este respins. admishj: Cele mai mari rate de eșec (30 sau mai multe puncte) din grupCucu energie de deplasare mai mare sunt mai frecvente decât în ​​grupul cu energie de deplasare mai mică (p=0,008).

Astfel, am putut demonstra astaVgrupCudeplasarea mai viguroasă este dominată de valorile extreme ale indicatorului de insuficiență și de faptul că acest indicator este mai mare decât valorile saleajungeîn acest grup special.

Acum am putea încerca să demonstrăm că în grupul cu o energie de deplasare mai mare, valorile mai mici ale indicelui de insuficiență sunt, de asemenea, mai frecvente, în ciuda faptului că valoarea medieV acest grup mai mult (26,11 față de 15,42 în grupCu deplasare mai mică).

Să formulăm ipoteze.

H 0 : Cele mai scăzute scoruri de malnutriție (nulă) din grupCu energie de deplasare mai mare se găsesc nu mai des decât în ​​grupCu energie de deplasare mai mică.

H 1 : Cele mai scăzute rate de malnutriție (nulă).V grupul cu energie de deplasare mai mare mai des decât în ​​grupCu deplasare mai puțin energetică. Să grupăm datele într-un nou tabel cu patru celule.

Tabelul 5.7

Un tabel cu patru celule pentru compararea grupurilor cu diferite energii de deplasare în ceea ce privește frecvența valorilor zero ale indicelui de deficiență

Grupuri	„Există un efect”: indicatorul insuficienței este 0		Eșec „Fără efect”.	exponentul nu este 0	Sume
Grupa 1 - cu energie de deplasare mai mare		(27,8%)		(72,2%)
1 grup - cu energie de deplasare mai mică		(8,3%)		(91,7%)
Sume

Determinăm valorile lui φ și calculăm valoarea lui φ*:

Răspuns: H 0 respins. Cele mai mici scoruri ale deficienței (nul) în grupul cu energie de deplasare mai mare sunt mai frecvente decât în ​​grupul cu energie de deplasare mai mică (p<0,05).

În concluzie, rezultatele obținute pot fi considerate ca dovada unei coincidențe parțiale a conceptelor de complex de Z. Freud și A. Adler.

Semnificativ este faptul că între indicatorul energiei de deplasare și indicatorul intensității sentimentului de insuficiență proprie, în întregul eșantion, s-a obținut o corelație liniară pozitivă (p = +0,491, p<0,01). Как мы можем убедиться, применение критерия φ* позволяет проникнуть в более тонкие и содержательно значимые соотношения между этими двумя показателями.

Exemplul 4 - utilizarea criteriului φ* în combinație cu criteriul λ Kolmogorov-Smirnov pentru a atinge maximul exacterezultat

Dacă eșantioanele sunt comparate după niște indicatori măsurați cantitativ, se pune problema identificării punctului de distribuție care poate fi folosit ca unul critic la împărțirea tuturor subiecților în cei „care au efect” și cei care „nu au efect”.

În principiu, punctul în care am împărți grupul în subgrupuri, unde există un efect și nu există efect, poate fi ales destul de arbitrar. Putem fi interesați de orice efect și, prin urmare, putem împărți ambele mostre în două părți în orice moment, atâta timp cât are sens.

Pentru a maximiza puterea testului φ*, totuși, este necesar să alegeți punctul în care diferențele dintre cele două grupuri comparate sunt cele mai mari. Mai exact, putem face acest lucru folosind algoritmul de calcul al criteriilorλ , care vă permite să găsiți punctul de discrepanță maximă între cele două mostre.

Posibilitatea combinarii criteriilor φ* siλ descris de E.V. Gubler (1978, p. 85-88). Să încercăm să folosim această metodă pentru a rezolva următoarea problemă.

Într-un studiu comun al lui M.A. Kurochkina, E.V. Sidorenko și Yu.A. Churakov (1992) în Marea Britanie, medicii generaliști englezi au fost chestionați în două categorii: a) medici care au susținut reforma medicală și și-au transformat deja cabinetele în organizații de sprijinire a fondurilor cu buget propriu; b) medici, ale căror recepții încă nu dispun de fonduri proprii și sunt asigurate integral de la bugetul de stat. Au fost trimise chestionare unui eșantion de 200 de medici, reprezentativ pentru populația generală de medici englezi în ceea ce privește reprezentarea persoanelor de sex, vârstă, vechime în muncă și loc de muncă diferit – în orașele mari sau în provincii.

Răspunsurile la chestionar au fost trimise de 78 de medici, 50 dintre ei lucrând în recepții cu fonduri și 28 în recepții fără fonduri. Fiecare dintre medici a trebuit să prezică care va fi ponderea recepțiilor cu fonduri în anul următor, 1993. Doar 70 de medici din 78 care au trimis răspunsuri au răspuns la această întrebare. Distribuția prognozelor acestora este prezentată în tabel. 5,8 separat pentru un grup de medici cu fonduri și un grup de medici fără fonduri.

Sunt cumva diferite predicțiile medicilor cu fonduri și ale medicilor fără fonduri?

Tabelul 5.8

Distribuția predicțiilor medicilor generaliști cu privire la cota de admitere cu fonduri în 1993

Cota estimată
săli de recepție cu fonduri	medici cu fond (n 1 =45)	medici fara fond (n 2 =25)	Sume
1. 0 până la 20%	4	5	9
2. 21 până la 40%	15	ȘI	26
3. 41 până la 60%	18	5	23
4. 61 până la 80%	7	4	ȘI
5. 81 până la 100%	1	0	1
Sume	45	25	70

Să determinăm punctul de discrepanță maximă dintre cele două distribuții de răspunsuri conform Algoritmului 15 din paragraful 4.3 (vezi Tabelul 5.9).

Tabelul 5.9

Calculul diferenței maxime de frecvențe acumulate în distribuțiile de prognoze ale medicilor din două grupe

Proporția proiectată de familii de plasament cu fonduri (%)	Frecvențele empirice pentru alegerea unei categorii de răspuns date		Frecvențe empirice		Frecvențe empirice cumulate		Diferență (d)
	medici cu fundatie(n 1 =45)	medici fara fond (n 2 =25)	f* uh 1	f* a2	∑f* e1	∑f* a1
1. 0 până la 20% 2. 21 până la 40% 3. 41 până la 60% 4. 61 până la 80% 5. 81 până la 100%	4 15 18 7 1	5 11 5 4 0	0,089 0,333 0,400 0,156 0,022	0,200 0,440 0,200 0,160 0	0,089 0,422 0,822 0,978 1,000	0,200 0,640 0,840 1,000 1,000	0111 0,218 0,018 0,022 0

Diferența maximă găsită între cele două frecvențe empirice acumulate este0,218.

Această diferență se acumulează în a doua categorie a prognozei. Să încercăm să folosim limita superioară a acestei categorii ca criteriu pentru împărțirea ambelor eșantioane într-un subgrup în care există un efect și un subgrup în care nu există efect. Vom presupune că există un „efect” dacă acest medic prezice de la 41 la 100% din sălile de recepție cu fonduri în1993 an, și că nu există „niciun efect” dacă un anumit medic prezice 0 până la 40% din operațiile cu fonduri în1993 an. Combinăm categoriile de prognoză 1 și 2, pe de o parte, și categoriile de prognoză 3, 4 și 5, pe de altă parte. Distribuția rezultată a prognozelor este prezentată în tabel. 5.10.

Tabelul 5.10

Repartizarea previziunilor pentru medicii cu fonduri și medicii fără fonduri

Ponderea proiectată a caselor de plasament cu fonduri (%1	Frecvențele empirice pentru alegerea unei anumite categorii de prognoză		Sume
	medici cu fundatie(n 1 =45)	medici fara fond(n 2 =25)
1. de la 0 la 40%	19	16	35
2. de la 41 la 100%	26	9	35
Sume	45	25	70

Putem folosi tabelul rezultat (Tabelul 5.10) testând diferite ipoteze prin compararea oricăror două dintre celulele sale. Ne amintim că acesta este așa-numitul tabel cu patru celule sau patru câmpuri.

În acest caz, ne interesează dacă medicii care au deja fonduri prevăd de fapt o mișcare mai mare în viitor decât medicii care nu au fonduri. Prin urmare, credem condiționat că există un „efect” atunci când prognoza se încadrează în categoria de la 41 la 100%. Pentru a simplifica calculele, acum trebuie să rotim masa cu 90°, rotindu-l în sensul acelor de ceasornic. Puteți chiar să o faceți literal, întorcând cartea împreună cu masa. Acum putem merge la foaia de lucru pentru calcularea criteriului φ* - transformarea unghiulară a lui Fisher.

Masa 5.11

Tabel cu patru celule pentru calcularea testului Fisher φ* pentru a identifica diferențele în prognozele a două grupuri de medici generaliști

grup	Există un efect - prognoză de la 41 la 100%	Niciun efect - prognoză de la 0 la 40%	Total
eugrupa – medici care au luat fondul	26 (57.8%)	19 (42.2%)	45
IIgrupa - medici care nu au luat fondul	9 (36.0%)	16 (64.0%)	25
Total	35	35	70

Să formulăm ipoteze.

H 0 : Procent de persoaneprezicerea repartizării fondurilor cu 41%-100% din toate recepțiile medicale, în grupul medicilor cu fonduri, nu există mai mult decât în ​​grupul medicilor fără fonduri.

H 1 : Proporția persoanelor care prevăd repartizarea fondurilor cu 41%-100% din toate recepțiile în grupul de medici cu fonduri este mai mare decât în ​​grupul de medici fără fonduri.

Determinăm valorile lui φ 1 și φ 2 conform tabeluluiXIIAnexa 1. Reamintim că φ 1 este întotdeauna unghiul corespunzător procentului mai mare.

Acum să determinăm valoarea empirică a criteriului φ*:

Conform Tabelului.XIIIAnexa 1 determină ce nivel de semnificație îi corespunde această valoare: p=0,039.

Conform aceluiași tabel din Anexa 1, se pot determina valorile critice ale criteriului φ*:

Răspuns: Dar respins (p=0,039). Procentul de oameni care prezic distribuirea fondurilor către41-100 % a tuturor recepţioniştilor, din lotul medicilor care au luat fondul, depăşeşte această pondere în lotul medicilor care nu au luat fondul.

Cu alte cuvinte, medicii care lucrează deja în cabinetele lor cu un buget separat prevăd că această practică va fi mai răspândită în acest an decât medicii care nu au fost încă de acord să treacă la un buget separat. Interpretările acestui rezultat sunt foarte apreciate. De exemplu, se poate presupune că medicii fiecăruia dintre grupuri consideră subconștient comportamentul lor ca fiind mai tipic. Ar putea însemna, de asemenea, că medicii care au trecut deja la un buget autosusținut tind să exagereze sfera acestei mișcări, deoarece trebuie să își justifice decizia. Diferențele relevate pot însemna, de asemenea, ceva care este complet dincolo de sfera întrebărilor puse în studiu. De exemplu, că activitatea medicilor care lucrează la buget independent contribuie la acutizarea diferențelor de poziții ale ambelor grupuri. Au fost foarte activi când au acceptat să ia fondurile, au fost foarte activi când și-au dat osteneala să răspundă la chestionarul prin poștă; sunt mai activi atunci când prevăd că alți medici vor fi mai activi în primirea fondurilor.

Într-un fel sau altul, putem fi siguri că nivelul diferențelor statistice găsite este maxim posibil pentru aceste date reale. Am stabilit cu ajutorul criteriuluiλ punctul de discrepanță maximă între cele două distribuții și tocmai în acest moment eșantioanele au fost împărțite în două părți.

Amprenta ta.