Distribuție binomială. Distribuții discrete în MS EXCEL
Distribuție binomială- una dintre cele mai importante distribuții de probabilitate de schimbare discretă variabilă aleatorie. Distribuția binomială este distribuția de probabilitate a unui număr m eveniment A V n observații reciproc independente. Adesea un eveniment A numit „succes” al observației, iar evenimentul opus - „eșec”, dar această desemnare este foarte condiționată.
Termenii distribuției binomiale:
- efectuate in totalitate n procese în care evenimentul A poate sau nu să apară;
- eveniment Aîn fiecare dintre încercări pot apărea cu aceeași probabilitate p;
- testele sunt independente reciproc.
Probabilitatea ca în n eveniment de testare A exact m ori, poate fi calculat folosind formula Bernoulli:
![]()
![]() ,
,
Unde p- probabilitatea producerii evenimentului A;
q = 1 - p este probabilitatea ca evenimentul opus să se producă.
Să ne dăm seama de ce distribuția binomială este legată de formula Bernoulli în modul descris mai sus . Eveniment - numărul de succese la n testele sunt împărțite într-un număr de opțiuni, în fiecare dintre acestea succesul este obținut în mîncercări și eșec - în n - m teste. Luați în considerare una dintre aceste opțiuni - B1 . Conform regulii adunării probabilităților, înmulțim probabilitățile evenimentelor opuse:
![]() ,
,
iar dacă notăm q = 1 - p, Acea
![]() .
.
Aceeași probabilitate va avea orice altă opțiune în care m succes și n - m eșecuri. Numărul de astfel de opțiuni este egal cu numărul de moduri în care este posibil n test get m succes.
Suma probabilităților tuturor m numărul evenimentului A(numerele de la 0 la n) este egal cu unu:
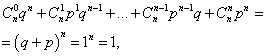
unde fiecare termen este un termen al binomului Newton. Prin urmare, distribuția considerată se numește distribuție binomială.
În practică, este adesea necesar să se calculeze probabilitățile „cel mult m succes in n teste” sau „cel puțin m succes in n teste". Pentru aceasta se folosesc următoarele formule.
Funcția integrală, adică probabilitate F(m) că în n eveniment de observare A nu va mai veni m o singura data, poate fi calculat folosind formula:
La randul lui probabilitate F(≥m) că în n eveniment de observare A vino măcar m o singura data, se calculează prin formula:
Uneori este mai convenabil să se calculeze probabilitatea ca în n eveniment de observare A nu va mai veni m ori, prin probabilitatea evenimentului opus:
![]() .
.
Care dintre formule să folosiți depinde de care dintre ele conține mai puțini termeni.
Caracteristicile distribuției binomiale se calculează folosind următoarele formule .
Valorea estimata: .
dispersie: .
Deviație standard: .
Distribuție binomială și calcule în MS Excel
Probabilitatea distribuției binomiale P n ( m) și valoarea funcției integrale F(m) poate fi calculat folosind funcția MS Excel BINOM.DIST. Fereastra pentru calculul corespunzător este prezentată mai jos (faceți clic pe butonul stâng al mouse-ului pentru a mări).

MS Excel vă solicită să introduceți următoarele date:
- numărul de succese;
- numărul de teste;
- probabilitatea de succes;
- integrală - valoare logică: 0 - dacă trebuie să calculați probabilitatea P n ( m) și 1 - dacă probabilitatea F(m).
Exemplul 1 Managerul companiei a rezumat informații despre numărul de camere vândute în ultimele 100 de zile. Tabelul rezumă informațiile și calculează probabilitățile ca un anumit număr de camere să fie vândute pe zi.
Ziua se încheie cu un profit dacă sunt vândute 13 sau mai multe camere. Probabilitatea ca ziua să fie calculată cu profit:
![]()
Probabilitatea ca ziua să fie lucrată fără profit:
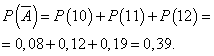
Fie ca probabilitatea ca ziua să fie calculată cu profit să fie constantă și egală cu 0,61, iar numărul de camere vândute pe zi nu depinde de zi. Apoi puteți utiliza distribuția binomială, unde evenimentul A- ziua va fi calculată cu profit, - fără profit.
Probabilitatea ca din 6 zile toate să fie rezolvate cu profit:
![]() .
.
Obținem același rezultat folosind funcția MS Excel BINOM.DIST (valoarea valorii integrale este 0):
P 6 (6 ) = BINOM.DIST(6; 6; 0,61; 0) = 0,052.
Probabilitatea ca din 6 zile 4 sau mai multe zile să fie lucrate cu profit:
Unde ![]() ,
,
![]() ,
,
Folosind funcția MS Excel BINOM.DIST, calculăm probabilitatea ca din 6 zile nu mai mult de 3 zile să fie finalizate cu profit (valoarea valorii integrale este 1):
P 6 (≤3 ) = BINOM.DIST(3, 6, 0,61, 1) = 0,435.
Probabilitatea ca din 6 zile toate să fie rezolvate cu pierderi:
![]() ,
,
Calculăm același indicator folosind funcția MS Excel BINOM.DIST:
P 6 (0 ) = BINOM.DIST(0; 6; 0,61; 0) = 0,0035.
Rezolvați singur problema și apoi vedeți soluția
Exemplul 2 O urna contine 2 bile albe si 3 negre. Se scoate o minge din urna, se pune culoarea si se pune la loc. Încercarea se repetă de 5 ori. Numărul de apariții de bile albe este o variabilă aleatorie discretă X, distribuit conform legii binomului. Alcătuiți legea distribuției unei variabile aleatoare. Definiți moda valorea estimatași dispersie.
Continuăm să rezolvăm problemele împreună
Exemplul 3 De la serviciul de curierat a mers la obiecte n= 5 curieri. Fiecare curier cu o probabilitate p= 0,3 este întârziat pentru obiect, indiferent de celelalte. Variabilă aleatorie discretă X- numarul de curieri intarziati. Construiți o serie de distribuție a acestei variabile aleatoare. Găsiți așteptările sale matematice, varianța, abaterea standard. Găsiți probabilitatea ca cel puțin doi curieri să întârzie obiectele.
Luați în considerare distribuția binomială, calculați așteptarea, varianța, modul ei matematic. Folosind funcția MS EXCEL BINOM.DIST(), vom reprezenta graficul funcției de distribuție și al densității probabilității. Să estimăm parametrul de distribuție p, așteptarea matematică a distribuției și abaterea standard. Luați în considerare și distribuția Bernoulli.
Definiție. Lasă-le să fie ținute n teste, în fiecare dintre ele pot apărea doar 2 evenimente: evenimentul „succes” cu o probabilitate p sau evenimentul „eşec” cu probabilitatea q =1-p (așa-numitul Schema Bernoulli,Bernoulliîncercări).
Probabilitatea de a obține exact X succes in acestea n teste este egal cu:
Numărul de succese din eșantion X este o variabilă aleatoare care are Distribuție binomială(Engleză) Binomdistributie) pȘi n– sunt parametri ai acestei distribuţii.
Amintiți-vă că pentru a aplica Scheme Bernoulliși în mod corespunzător distribuție binomială, trebuie îndeplinite următoarele condiții:
- fiecare încercare trebuie să aibă exact două rezultate, numite condiționat „succes” și „eșec”.
- rezultatul fiecărui test nu trebuie să depindă de rezultatele testelor anterioare (independența testului).
- rata de succes p ar trebui să fie constantă pentru toate testele.
Distribuție binomială în MS EXCEL
În MS EXCEL, începând cu versiunea 2010, pt Distribuție binomială există o funcție BINOM.DIST() , titlu englezesc- BINOM.DIST(), care vă permite să calculați probabilitatea ca eșantionul să fie exact X„succesuri” (adică funcția de densitate de probabilitate p(x), vezi formula de mai sus) și funcția de distribuție integrală(probabilitatea ca eșantionul să aibă X sau mai puține „reușite”, inclusiv 0).
Înainte de MS EXCEL 2010, EXCEL avea funcția BINOMDIST(), care vă permite, de asemenea, să calculați funcția de distribuțieȘi probabilitate densitate p(x). BINOMDIST() este lăsat în MS EXCEL 2010 pentru compatibilitate.
Fișierul exemplu conține grafice densitatea distribuției de probabilitateȘi .

Distribuție binomială are denumirea B(n; p) .
Notă: Pentru constructii funcția de distribuție integrală tip grafic de potrivire perfectă Programa, Pentru densitatea distributiei – Histogramă cu grupare. Pentru mai multe informații despre construirea diagramelor, citiți articolul Principalele tipuri de diagrame.
Notă: Pentru confortul scrierii formulelor în fișierul exemplu, au fost create Nume pentru parametri Distribuție binomială: n și p.

Fișierul exemplu arată diferite calcule de probabilitate folosind funcțiile MS EXCEL:

După cum se vede în imaginea de mai sus, se presupune că:
- Populația infinită din care este făcut eșantionul conține 10% (sau 0,1) elemente bune (parametru p, al treilea argument al funcției =BINOM.DIST() )
- Pentru a calcula probabilitatea ca într-un eșantion de 10 elemente (parametrul n, al doilea argument al funcției) vor fi exact 5 elemente valide (primul argument), trebuie să scrieți formula: =BINOM.DIST(5; 10; 0,1; FALSE)
- Ultimul, al patrulea element este setat = FALSE, i.e. valoarea funcției este returnată densitatea distributiei.
Dacă valoarea celui de-al patrulea argument = TRUE, atunci funcția BINOM.DIST() returnează valoarea funcția de distribuție integrală sau pur și simplu funcția de distribuție. În acest caz, puteți calcula probabilitatea ca numărul de elemente bune din eșantion să fie dintr-un anumit interval, de exemplu, 2 sau mai puțin (inclusiv 0).
Pentru a face acest lucru, trebuie să scrieți formula:
= BINOM.DIST(2; 10; 0,1; TRUE)
Notă: Pentru o valoare neîntregătoare a lui x, . De exemplu, următoarele formule vor returna aceeași valoare:
=BINOM.DIST( 2
; 10; 0,1; ADEVĂRAT)
=BINOM.DIST( 2,9
; 10; 0,1; ADEVĂRAT)
Notă: În fișierul exemplu probabilitate densitateȘi funcția de distribuție de asemenea, calculat folosind definiția și funcția COMBIN().
Indicatori de distribuție
ÎN fișier exemplu pe foaie Exemplu există formule pentru calcularea unor indicatori de distribuție:
- =n*p;
- (abaterea standard pătrată) = n*p*(1-p);
- = (n+1)*p;
- =(1-2*p)*ROOT(n*p*(1-p)).
Deducem formula așteptări matematice Distribuție binomială folosind Schema Bernoulli.
Prin definiție, o variabilă aleatoare X în Schema Bernoulli(variabilă aleatoare Bernoulli) are funcția de distribuție:

Această distribuție se numește distribuția Bernoulli.
Notă: distribuția Bernoulli- caz special Distribuție binomială cu parametrul n=1.
Să generăm 3 matrice de 100 de numere cu diferite probabilități de succes: 0,1; 0,5 și 0,9. Pentru a face acest lucru, în fereastră Generarea numerelor aleatorii setați următorii parametri pentru fiecare probabilitate p:

Notă: Dacă setați opțiunea Imprăștire aleatorie (Sămânță aleatorie), apoi puteți alege un anumit set aleatoriu de numere generate. De exemplu, setând această opțiune =25, puteți genera aceleași seturi de numere aleatorii pe computere diferite (dacă, desigur, alți parametri de distribuție sunt aceiași). Valoarea opțiunii poate lua valori întregi de la 1 la 32 767. Numele opțiunii Imprăștire aleatorie poate deruta. Ar fi mai bine să o traducem ca Setați un număr cu numere aleatorii.
Ca urmare, vom avea 3 coloane de 100 de numere, pe baza cărora, de exemplu, putem estima probabilitatea de succes p dupa formula: Număr de succese/100(cm. exemplu de fișă de fișier Generarea lui Bernoulli).

Notă: Pentru distribuții Bernoulli cu p=0,5, puteți folosi formula =RANDBETWEEN(0;1) , care corespunde cu .
Generarea numerelor aleatorii. Distribuție binomială
Să presupunem că există 7 articole defecte în eșantion. Aceasta înseamnă că este „foarte probabil” ca proporția produselor defecte să se fi schimbat. p, care este o caracteristică a procesului nostru de producție. Deși această situație este „foarte probabilă”, există o posibilitate (risc alfa, eroare de tip 1, „alarma falsă”) ca p a rămas neschimbată, iar numărul crescut de produse defecte s-a datorat prelevării aleatorii.
După cum se poate observa în figura de mai jos, 7 este numărul de produse defecte care este acceptabil pentru un proces cu p=0,21 la aceeași valoare Alfa. Acest lucru ilustrează faptul că, atunci când pragul de articole defecte dintr-o probă este depășit, p„probabil” a crescut. Expresia „cel mai probabil” înseamnă că există doar o șansă de 10% (100%-90%) ca abaterea procentului de produse defecte peste prag să se datoreze doar unor cauze aleatorii.

Astfel, depășirea numărului prag de produse defecte din probă poate servi drept semnal că procesul a devenit deranjat și a început să producă b O procent mai mare de produse defecte.
Notă: Înainte de MS EXCEL 2010, EXCEL avea o funcție CRITBINOM() , care este echivalentă cu BINOM.INV() . CRITBINOM() este lăsat în MS EXCEL 2010 și mai sus pentru compatibilitate.
Relația distribuției binomiale cu alte distribuții
Dacă parametrul n Distribuție binomială tinde spre infinit şi p tinde spre 0, atunci în acest caz Distribuție binomială poate fi aproximată.
Este posibil să se formuleze condiții când aproximarea Distribuția Poisson functioneaza bine:
- p<0,1 (mai putin pși altele n, cu atât aproximarea este mai precisă);
- p>0,9 (având în vedere că q=1- p, calculele în acest caz trebuie efectuate folosind q(A X trebuie inlocuit cu n- X). Prin urmare, cu atât mai puțin qși altele n, cu atât aproximarea este mai precisă).
La 0,1<=p<=0,9 и n*p>10 Distribuție binomială poate fi aproximată.
La randul lui, Distribuție binomială poate servi ca o bună aproximare atunci când dimensiunea populației este N Distribuție hipergeometrică mult mai mare decât dimensiunea eșantionului n (adică N>>n sau n/N<<1).
Puteți citi mai multe despre relația dintre distribuțiile de mai sus în articol. Acolo sunt date și exemple de aproximare, iar condițiile sunt explicate când este posibil și cu ce precizie.
SFAT: Puteți citi despre alte distribuții ale MS EXCEL în articol.
Spre deosebire de distribuțiile normale și uniforme, care descriu comportamentul unei variabile în eșantionul de subiecți studiati, distribuția binomială este utilizată în alte scopuri. Acesta servește la prezicerea probabilității a două evenimente care se exclud reciproc într-un anumit număr de încercări independente. Un exemplu clasic de distribuție binomială este aruncarea unei monede care cade pe o suprafață dură. Două rezultate (evenimente) sunt la fel de probabile: 1) moneda cade „vultur” (probabilitatea este egală cu R) sau 2) moneda cade „cozi” (probabilitatea este egală cu q). Dacă nu se dă un al treilea rezultat, atunci p = q= 0,5 și p + q= 1. Folosind formula de distribuție binomială, puteți determina, de exemplu, care este probabilitatea ca în 50 de încercări (numărul de aruncări de monede) ultima să cadă cu capul, să zicem, de 25 de ori.
Pentru raționament suplimentar, introducem notația general acceptată:
n este numărul total de observații;
i- numărul de evenimente (rezultate) care ne interesează;
n – i– numărul de evenimente alternative;
p- probabilitatea determinată empiric (uneori - asumată) a unui eveniment de interes pentru noi;
q este probabilitatea unui eveniment alternativ;
P n ( i) este probabilitatea prezisă a evenimentului care ne interesează i pentru un anumit număr de observații n.
Formula de distribuție binomială:
În cazul unui rezultat echiprobabil al evenimentelor ( p = q) puteți folosi formula simplificată:
![]() (6.8)
(6.8)
Să luăm în considerare trei exemple care ilustrează utilizarea formulelor de distribuție binomială în cercetarea psihologică.
Exemplul 1
Să presupunem că 3 elevi rezolvă o problemă de complexitate crescută. Pentru fiecare dintre ele, 2 rezultate sunt la fel de probabile: (+) - soluție și (-) - nerezolvarea problemei. În total, sunt posibile 8 rezultate diferite (2 3 = 8).
Probabilitatea ca niciun elev să nu facă față sarcinii este de 1/8 (opțiunea 8); 1 elev va îndeplini sarcina: P= 3/8 (opțiunile 4, 6, 7); 2 elevi - P= 3/8 (opțiunile 2, 3, 5) și 3 elevi – P=1/8 (opțiunea 1).
Este necesar să se determine probabilitatea ca trei din 5 elevi să facă față cu succes acestei sarcini.
Soluţie
Total de rezultate posibile: 2 5 = 32.
Numărul total de opțiuni 3(+) și 2(-) este

Prin urmare, probabilitatea rezultatului așteptat este 10/32 » 0,31.
Exemplul 3
Exercițiu
Determinați probabilitatea ca 5 extrovertiți să fie găsiți într-un grup de 10 subiecți la întâmplare.
Soluţie
1. Introduceți notația: p=q= 0,5; n= 10; i = 5; P 10 (5) = ?
2. Folosim o formulă simplificată (vezi mai sus):
Concluzie
Probabilitatea ca 5 extrovertiți să fie găsiți la 10 subiecți aleatoriu este de 0,246.
Note
1. Calculul prin formula cu un număr suficient de mare de încercări este destul de laborios, de aceea, în aceste cazuri, se recomandă utilizarea tabelelor de distribuție binomială.
2. În unele cazuri, valorile pȘi q poate fi setat inițial, dar nu întotdeauna. De regulă, acestea sunt calculate pe baza rezultatelor testelor preliminare (studii pilot).
3. Într-o imagine grafică (în coordonate P n(i) = f(i)) distribuţia binomială poate avea diferite forme: în cazul p = q distribuția este simetrică și seamănă cu distribuția normală Gaussiană; asimetria distribuției este mai mare, cu atât diferența dintre probabilități este mai mare pȘi q.
Distribuția Poisson
Distribuția Poisson este un caz special al distribuției binomiale, utilizată atunci când probabilitatea evenimentelor de interes este foarte scăzută. Cu alte cuvinte, această distribuție descrie probabilitatea unor evenimente rare. Formula Poisson poate fi folosită pentru p < 0,01 и q ≥ 0,99.
Ecuația Poisson este aproximativă și este descrisă prin următoarea formulă:
![]() (6.9)
(6.9)
unde μ este produsul dintre probabilitatea medie a evenimentului și numărul de observații.
Ca exemplu, luați în considerare algoritmul pentru rezolvarea următoarei probleme.
Sarcina
Timp de câțiva ani, în 21 de clinici mari din Rusia, a fost efectuată o examinare în masă a nou-născuților pentru boala sugarilor cu boala Down (eșantionul a fost în medie de 1000 de nou-născuți în fiecare clinică). Au fost primite următoarele date:
Exercițiu
1. Determinați probabilitatea medie a bolii (din punct de vedere al numărului de nou-născuți).
2. Determinați numărul mediu de nou-născuți cu o boală.
3. Determinați probabilitatea ca între 100 de nou-născuți selectați aleatoriu să fie 2 bebeluși cu boala Down.
Soluţie
1. Determinați probabilitatea medie a bolii. În acest sens, trebuie să ne ghidăm după următorul raționament. Boala Down a fost inregistrata doar in 10 clinici din 21. Nu au fost gasite boli in 11 clinici, 1 caz in 6 clinici, 2 cazuri in 2 clinici, 3 in clinica I si 4 cazuri in clinica I. 5 cazuri nu au fost găsite în nicio clinică. Pentru a determina probabilitatea medie a bolii, este necesar să se împartă numărul total de cazuri (6 1 + 2 2 + 1 3 + 1 4 = 17) la numărul total de nou-născuți (21000):
![]()
2. Numărul de nou-născuți care reprezintă o boală este reciproca probabilității medii, adică egal cu numărul total de nou-născuți împărțit la numărul de cazuri înregistrate:
![]()
3. Înlocuiți valorile p = 0,00081, n= 100 și i= 2 în formula Poisson:
Răspuns
Probabilitatea ca dintre 100 de nou-născuți selectați aleatoriu să se găsească 2 sugari cu boala Down este de 0,003 (0,3%).
Sarcini conexe
Sarcina 6.1
Exercițiu
Folosind datele problemei 5.1 privind timpul reacției senzorio-motorii, se calculează asimetria și curtoza distribuției VR.
Sarcina 6. 2
200 de absolvenți au fost testați pentru nivelul de inteligență ( IQ). După normalizarea distribuţiei rezultate IQ conform abaterii standard s-au obtinut urmatoarele rezultate:
Exercițiu
Folosind testele Kolmogorov și chi-pătrat, determinați dacă distribuția rezultată a indicatorilor corespunde cu IQ normal.
Sarcina 6. 3
La un subiect adult (un bărbat de 25 de ani), a fost studiat timpul unei reacții senzoriomotorii simple (SR) ca răspuns la un stimul sonor cu o frecvență constantă de 1 kHz și o intensitate de 40 dB. Stimulul a fost prezentat de o sută de ori la intervale de 3-5 secunde. Valorile individuale VR pentru 100 de repetări au fost distribuite după cum urmează:
Exercițiu
1. Construiți o histogramă de frecvență a distribuției VR; determinați valoarea medie a VR și valoarea abaterii standard.
2. Calculați coeficientul de asimetrie și curtoza distribuției BP; pe baza valorilor primite La fel deȘi Ex faceți o concluzie despre conformitatea sau nerespectarea acestei distribuții cu cea normală.
Sarcina 6.4
În 1998, 14 persoane (5 băieți și 9 fete) au absolvit școlile din Nijni Tagil cu medalii de aur, 26 de persoane (8 băieți și 18 fete) cu medalii de argint.
Întrebare
Se poate spune că fetele primesc medalii mai des decât băieții?
Notă
Raportul dintre numărul de băieți și fete din populația generală este considerat egal.
Sarcina 6.5
Se crede că numărul de extrovertiți și introvertiți dintr-un grup omogen de subiecți este aproximativ același.
Exercițiu
Determinați probabilitatea ca într-un grup de 10 subiecți aleși aleatoriu să se găsească 0, 1, 2, ..., 10 extrovertiți. Construiți o expresie grafică pentru distribuția probabilității de a găsi 0, 1, 2, ..., 10 extrovertiți într-un grup dat.
Sarcina 6.6
Exercițiu
Calculați probabilitatea P n(i) funcții de distribuție binomială pentru p= 0,3 și q= 0,7 pentru valori n= 5 și i= 0, 1, 2, ..., 5. Construiți o expresie grafică a dependenței P n(i) = f(i) .
Sarcina 6.7
În ultimii ani, credința în prognozele astrologice s-a impus în rândul unei anumite părți a populației. Conform rezultatelor sondajelor preliminare, s-a constatat că aproximativ 15% din populație crede în astrologie.
Exercițiu
Determinați probabilitatea ca printre 10 respondenți selectați aleatoriu să fie 1, 2 sau 3 persoane care cred în prognozele astrologice.
Sarcina 6.8
Sarcina
În 42 de școli secundare din orașul Ekaterinburg și regiunea Sverdlovsk (numărul total de elevi este de 12.260), a fost dezvăluit următorul număr de cazuri de boală mintală în rândul elevilor de-a lungul mai multor ani:
Exercițiu
Să fie examinați aleatoriu 1000 de școlari. Calculați care este probabilitatea ca 1, 2 sau 3 copii bolnavi mintal să fie identificați printre această mie de școlari?
SECȚIUNEA 7. MĂSURI DE DIFERENȚĂ
Formularea problemei
Să presupunem că avem două eșantioane independente de subiecți XȘi la. Independent probele sunt numărate atunci când același subiect (subiect) apare într-un singur eșantion. Sarcina este de a compara aceste eșantioane (două seturi de variabile) între ele pentru diferențele lor. Desigur, oricât de apropiate sunt valorile variabilelor din primul și al doilea eșantion, unele, chiar dacă nesemnificative, vor fi detectate diferențe între ele. Din punct de vedere al statisticii matematice, ne interesează întrebarea dacă diferențele dintre aceste eșantioane sunt semnificative statistic (semnificative statistic) sau nesigure (aleatoare).
Cele mai comune criterii pentru semnificația diferențelor dintre eșantioane sunt măsurile parametrice ale diferențelor - Criteriul elevuluiȘi criteriul lui Fisher. În unele cazuri, sunt utilizate criterii neparametrice - Testul Q al lui Rosenbaum, testul U Mann-Whitney si altii. Transformată unghiulară Fisher φ*, care vă permit să comparați valorile exprimate în procente (procente) între ele. Și, în sfârșit, ca caz special, pentru a compara eșantioanele, pot fi utilizate criterii care caracterizează forma distribuțiilor eșantioanelor - criteriul χ 2 PearsonȘi criteriul λ Kolmogorov – Smirnov.
Pentru a înțelege mai bine acest subiect, vom proceda după cum urmează. Vom rezolva aceeași problemă cu patru metode folosind patru criterii diferite - Rosenbaum, Mann-Whitney, Student și Fisher.
Sarcina
30 de elevi (14 băieți și 16 fete) în timpul sesiunii de examene au fost testați conform testului Spielberger pentru nivelul de anxietate reactivă. S-au obţinut următoarele rezultate (Tabelul 7.1):
Tabelul 7.1
| Subiecte | Nivel de anxietate reactiv | |||||||||||||||
| Tineri | ||||||||||||||||
| fetelor |
Exercițiu
Pentru a determina dacă diferențele în nivelul de anxietate reactivă la băieți și fete sunt semnificative statistic.
Sarcina pare a fi destul de tipică pentru un psiholog specializat în domeniul psihologiei educaționale: cine experimentează mai acut stresul de la examen - băieți sau fete? Dacă diferențele dintre eșantioane sunt semnificative statistic, atunci există diferențe semnificative de gen în acest aspect; dacă diferențele sunt aleatorii (nu sunt semnificative din punct de vedere statistic), această ipoteză trebuie eliminată.
7. 2. Test neparametric Q Rosenbaum
Q- Criteriul lui Rozenbaum se bazează pe compararea serii de valori „suprapuse” una pe cealaltă a două variabile independente. În același timp, nu este analizată natura distribuției trăsăturii în cadrul fiecărui rând - în acest caz contează doar lățimea secțiunilor care nu se suprapun din cele două rânduri clasate. Când comparăm două serii de variabile clasificate între ele, sunt posibile 3 opțiuni:
1. Ranguri clasate XȘi y nu au o zonă de suprapunere, adică toate valorile primei serii clasate ( X) este mai mare decât toate valorile seriei clasate a doua ( y):
În acest caz, diferențele dintre eșantioane, determinate de orice criteriu statistic, sunt cu siguranță semnificative, iar utilizarea criteriului Rosenbaum nu este necesară. Cu toate acestea, în practică, această opțiune este extrem de rară.
2. Rândurile clasate se suprapun complet între ele (de regulă, unul dintre rânduri este în interiorul celuilalt), nu există zone care nu se suprapun. În acest caz, criteriul Rosenbaum nu este aplicabil.

3. Există o zonă suprapusă a rândurilor, precum și două zone care nu se suprapun ( N 1Și N 2) în legătură cu diferit serii clasate (notăm X- un rând deplasat spre mare, y- în direcția valorilor inferioare):

Acest caz este tipic pentru utilizarea criteriului Rosenbaum, atunci când se utilizează următoarele condiții trebuie respectate:
1. Volumul fiecărei probe trebuie să fie de cel puțin 11.
2. Dimensiunile mostrelor nu trebuie să difere semnificativ unele de altele.
Criteriu Q Rosenbaum corespunde numărului de valori care nu se suprapun: Q = N 1 +N 2 . Concluzia despre fiabilitatea diferențelor dintre eșantioane se face dacă Q > Q kr . În același timp, valorile Q cr sunt în tabele speciale (vezi Anexa, Tabelul VIII).
Să revenim la sarcina noastră. Să introducem notația: X- o selecție de fete, y- O selecție de băieți. Pentru fiecare probă, construim o serie clasificată:
X: 28 30 34 34 35 36 37 39 40 41 42 42 43 44 45 46
y: 26 28 32 32 33 34 35 38 39 40 41 42 43 44
Numărăm numărul de valori din zonele care nu se suprapun din seria clasată. Consecutiv X valorile 45 și 46 nu se suprapun, adică N 1 = 2;la rând y doar 1 valoare care nu se suprapune 26 i.e. N 2 = 1. Prin urmare, Q = N 1 +N 2 = 1 + 2 = 3.
În tabel. VIII Anexă constatăm că Q kr . = 7 (pentru un nivel de semnificație de 0,95) și Q cr = 9 (pentru un nivel de semnificație de 0,99).
Concluzie
Deoarece Q<Q cr, apoi conform criteriului Rosenbaum, diferențele dintre eșantioane nu sunt semnificative statistic.
Notă
Testul Rosenbaum poate fi utilizat indiferent de natura distribuției variabilelor, adică în acest caz, nu este nevoie să folosiți testele lui Pearson χ 2 și λ ale lui Kolmogorov pentru a determina tipul de distribuții în ambele eșantioane.
7. 3. U- Testul Mann-Whitney
Spre deosebire de criteriul Rosenbaum, U Testul Mann-Whitney se bazează pe determinarea zonei de suprapunere între două rânduri clasate, adică cu cât zona de suprapunere este mai mică, cu atât diferențele dintre probe sunt mai semnificative. Pentru aceasta, se folosește o procedură specială de conversie a scalelor de interval în scale de rang.
Să luăm în considerare algoritmul de calcul pentru U-criteriul pe exemplul sarcinii anterioare.
Tabelul 7.2
| X y | R X y | R X y * | R X | R y |
| 26 28 32 32 33 34 35 38 39 40 41 42 43 44 | 2,5 2,5 5,5 5,5 11,5 11,5 16,5 16,5 18,5 18,5 20,5 20,5 25,5 25,5 27,5 27,5 | 2,5 11,5 16,5 18,5 20,5 25,5 27,5 | 1 2,5 5,5 5,5 7 9 11,5 15 16,5 18,5 20,5 23 25,5 27,5 | |
| Σ | 276,5 | 188,5 |
1. Construim o singură serie clasată din două mostre independente. În acest caz, valorile pentru ambele probe sunt amestecate, coloana 1 ( X, y). Pentru a simplifica munca ulterioară (inclusiv în versiunea pentru computer), valorile pentru diferite mostre ar trebui să fie marcate în fonturi diferite (sau culori diferite), ținând cont de faptul că în viitor le vom posta în coloane diferite.
2. Transformați scara intervalului de valori într-una ordinală (pentru a face acest lucru, redesemnăm toate valorile cu numere de rang de la 1 la 30, coloana 2 ( R X y)).
3. Introducem corecții pentru rangurile aferente (aceleași valori ale variabilei sunt notate cu același rang, cu condiția ca suma rangurilor să nu se modifice, coloana 3 ( R X y *). În această etapă, se recomandă calcularea sumelor rangurilor din coloana a 2-a și a 3-a (dacă toate corecțiile sunt corecte, atunci aceste sume ar trebui să fie egale).
4. Împărțim numerele de rang în funcție de apartenența lor la un anumit eșantion (coloanele 4 și 5 ( R x și R y)).
5. Efectuăm calcule după formula:
![]() (7.1)
(7.1)
Unde T x este cea mai mare dintre sumele de rang ; n x și n y, respectiv, dimensiunile eșantionului. În acest caz, rețineți că dacă T X< T y , apoi notația XȘi y ar trebui inversat.
6. Comparați valoarea obținută cu cea tabelară (vezi Anexe, Tabelul IX) Concluzia despre fiabilitatea diferențelor dintre cele două eșantioane se face dacă U exp.< U cr. .
În exemplul nostru ![]() U exp. = 83,5 > U cr. = 71.
U exp. = 83,5 > U cr. = 71.
Concluzie
Diferențele dintre cele două probe conform testului Mann-Whitney nu sunt semnificative statistic.
Note
1. Testul Mann-Whitney practic nu are restricții; dimensiunile minime ale eșantioanelor comparate sunt de 2 și 5 persoane (vezi Tabelul IX din Anexă).
2. Similar testului Rosenbaum, testul Mann-Whitney poate fi utilizat pentru orice probe, indiferent de natura distribuției.
Criteriul elevului
Spre deosebire de criteriile Rosenbaum și Mann-Whitney, criteriul t Metoda studentului este parametrică, adică se bazează pe determinarea principalilor indicatori statistici - valorile medii din fiecare eșantion ( și ) și variațiile acestora (s 2 x și s 2 y), calculate folosind formule standard (a se vedea secțiunea 5).
Utilizarea criteriului Studentului presupune următoarele condiții:
1. Distribuțiile de valori pentru ambele eșantioane trebuie să respecte legea distributie normala(vezi secțiunea 6).
2. Volumul total al probelor trebuie să fie de cel puțin 30 (pentru β 1 = 0,95) și de cel puțin 100 (pentru β 2 = 0,99).
3. Volumele a două probe nu trebuie să difere semnificativ una de alta (nu mai mult de 1,5 ÷ 2 ori).
Ideea criteriului elevului este destul de simplă. Să presupunem că valorile variabilelor din fiecare dintre eșantioane sunt distribuite conform legii normale, adică avem de-a face cu două distribuții normale care diferă una de cealaltă ca valori medii și varianță (respectiv, și , și , vezi Fig. 7.1).

s X s y
Orez. 7.1. Estimarea diferențelor dintre două eșantioane independente: și - valorile medii ale eșantioanelor XȘi y; s x și s y - abateri standard
Este ușor de înțeles că diferențele dintre două eșantioane vor fi cu atât mai mari, cu atât diferența dintre medii este mai mare și cu atât variațiile (sau abaterile standard) ale acestora sunt mai mici.
În cazul probelor independente, coeficientul Student este determinat de formula:
 (7.2)
(7.2)
Unde n x și n y - respectiv, numărul de mostre XȘi y.
După calcularea coeficientului Student în tabelul valorilor standard (critice). t(vezi Anexa, Tabelul X) găsiți valoarea corespunzătoare numărului de grade de libertate n = n x + n y - 2 și comparați-l cu cel calculat prin formulă. Dacă t exp. £ t cr. , atunci se respinge ipoteza despre fiabilitatea diferenţelor dintre eşantioane, dacă t exp. > t cr. , atunci este acceptat. Cu alte cuvinte, eșantioanele sunt semnificativ diferite unele de altele dacă coeficientul Student calculat prin formulă este mai mare decât valoarea tabelară pentru nivelul de semnificație corespunzător.
În problema pe care am analizat-o mai devreme, calcularea valorilor medii și a variațiilor dă următoarele valori: X cf. = 38,5; σ x 2 = 28,40; la cf. = 36,2; σ y 2 = 31,72.
Se poate observa că valoarea medie a anxietății în grupul fetelor este mai mare decât în grupul băieților. Cu toate acestea, aceste diferențe sunt atât de mici încât este puțin probabil să fie semnificative statistic. Dispersarea valorilor la băieți, dimpotrivă, este puțin mai mare decât la fete, dar diferențele dintre variații sunt și ele mici.

Concluzie
t exp. = 1,14< t cr. = 2,05 (β 1 = 0,95). Diferențele dintre cele două eșantioane comparate nu sunt semnificative statistic. Această concluzie este destul de consistentă cu cea obținută folosind criteriile Rosenbaum și Mann-Whitney.
O altă modalitate de a determina diferențele dintre două eșantioane folosind testul t Student este de a calcula intervalul de încredere al abaterilor standard. Intervalul de încredere este abaterea pătrată medie (standard) împărțită la rădăcina pătrată a dimensiunii eșantionului și înmulțită cu valoarea standard a coeficientului Student pentru n– 1 grad de libertate (respectiv, și ).
Notă
Valoare = mx se numește eroarea pătratică medie (vezi Secțiunea 5). Prin urmare, intervalul de încredere este eroarea standard înmulțită cu coeficientul Student pentru o dimensiune dată de eșantion, unde numărul de grade de libertate ν = n- 1, și pentru nivelul dat semnificaţie.
Două eșantioane care sunt independente unele de altele sunt considerate a fi semnificativ diferite dacă intervalele de încredere pentru aceste eșantioane nu se suprapun. În cazul nostru, avem 38,5 ± 2,84 pentru primul eșantion și 36,2 ± 3,38 pentru al doilea.
Prin urmare, variații aleatorii x i se află în intervalul 35,66 ¸ 41,34 și variații y eu- în intervalul 32,82 ¸ 39,58. Pe baza acestui fapt, se poate afirma că diferențele dintre probe XȘi y nesigure din punct de vedere statistic (intervalele de variații se suprapun unele cu altele). În acest caz, trebuie avut în vedere că lățimea zonei de suprapunere în acest caz nu contează (important este doar faptul că se suprapun intervalele de încredere).
Metoda studentului pentru eșantioane interdependente (de exemplu, pentru a compara rezultatele obținute în urma testărilor repetate pe același eșantion de subiecți) este folosită destul de rar, deoarece există alte tehnici statistice, mai informative în aceste scopuri (vezi Secțiunea 10). Cu toate acestea, în acest scop, ca primă aproximare, puteți utiliza formula Student de următoarea formă:
 (7.3)
(7.3)
Rezultatul obținut este comparat cu valoarea tabelului pt n– 1 grad de libertate, unde n– numărul de perechi de valori XȘi y. Rezultatele comparației sunt interpretate exact în același mod ca și în cazul calculării diferenței dintre două eșantioane independente.
criteriul lui Fisher
criteriul Fisher ( F) se bazează pe același principiu ca și testul t al lui Student, adică implică calcularea valorilor medii și a variațiilor în eșantioanele comparate. Este folosit cel mai adesea atunci când se compară eșantioane care sunt inegale ca mărime (diferite ca mărime) între ele. Testul Fisher este ceva mai riguros decât testul Student și, prin urmare, este mai preferabil în cazurile în care există îndoieli cu privire la fiabilitatea diferențelor (de exemplu, dacă, conform testului Student, diferențele sunt semnificative la zero și nu sunt semnificative la prima semnificație nivel).
Formula lui Fisher arată astfel:
 (7.4)
(7.4)
unde si  (7.5, 7.6)
(7.5, 7.6)
În problema noastră d2= 5,29; σz 2 = 29,94.
Înlocuiți valorile din formula: ![]()
În tabel. XI Aplicații, constatăm că pentru nivelul de semnificație β 1 = 0,95 și ν = n x + n y - 2 = 28 valoarea critică este 4,20.
Concluzie
F = 1,32 < F cr.= 4,20. Diferențele dintre eșantioane nu sunt semnificative statistic.
Notă
Când utilizați testul Fisher, trebuie îndeplinite aceleași condiții ca și pentru testul Student (vezi subsecțiunea 7.4). Cu toate acestea, este permisă diferența în numărul de probe de mai mult de două ori.
Astfel, atunci când rezolvăm aceeași problemă cu patru metode diferite folosind două criterii neparametrice și două criterii parametrice, am ajuns la concluzia fără echivoc că diferențele dintre grupul de fete și grupul de băieți în ceea ce privește nivelul de anxietate reactivă sunt nesigure (i.e. , sunt în variația aleatorie). Cu toate acestea, pot exista cazuri când nu este posibil să faceți o concluzie fără ambiguitate: unele criterii dau diferențe de încredere, altele - diferențe nesigure. În aceste cazuri, se acordă prioritate criteriilor parametrice (în funcție de suficiența dimensiunii eșantionului și de distribuția normală a valorilor studiate).
7. 6. Criteriul j* - Transformarea unghiulară a lui Fisher
Criteriul j*Fisher este conceput pentru a compara două eșantioane în funcție de frecvența de apariție a efectului de interes pentru cercetător. Evaluează semnificația diferențelor dintre procentele a două eșantioane în care se înregistrează efectul interesului. Compararea procentelor în cadrul aceluiași eșantion este, de asemenea, permisă.
esență transformare unghiulară Fisher trebuie să convertească procentele în unghiuri centrale, care sunt măsurate în radiani. Un procent mai mare va corespunde unui unghi mai mare j, și o cotă mai mică - un unghi mai mic, dar relația aici este neliniară:
![]()
Unde R– procent, exprimat în fracții de unitate.
Cu o creștere a discrepanței dintre unghiurile j 1 și j 2 și o creștere a numărului de eșantioane, valoarea criteriului crește.
Criteriul Fisher se calculează prin următoarea formulă:
| |
unde j 1 este unghiul corespunzător procentului mai mare; j 2 - unghiul corespunzător unui procent mai mic; n 1 și n 2 - respectiv, volumul primei și celei de-a doua probe.
Valoarea calculată prin formulă este comparată cu valoarea standard (j* st = 1,64 pentru b 1 = 0,95 și j* st = 2,31 pentru b 2 = 0,99. Diferențele dintre cele două eșantioane sunt considerate semnificative statistic dacă j*> j* st pentru un anumit nivel de semnificație.
Exemplu
Ne interesează dacă cele două grupuri de elevi diferă unul de celălalt în ceea ce privește succesul îndeplinirii unei sarcini destul de complexe. În primul grup de 20 de persoane, 12 studenți au făcut față, în al doilea - 10 persoane din 25.
Soluţie
1. Introduceți notația: n 1 = 20, n 2 = 25.
2. Calculați procente R 1 și R 2: R 1 = 12 / 20 = 0,6 (60%), R 2 = 10 / 25 = 0,4 (40%).
3. În tabel. XII Aplicații, găsim valorile lui φ corespunzătoare procentelor: j 1 = 1,772, j 2 = 1,369.
| |
De aici:
Concluzie
Diferențele dintre grupuri nu sunt semnificative statistic deoarece j*< j* ст для 1-го и тем более для 2-го уровня значимости.
7.7. Utilizând testul χ2 al lui Pearson și testul λ al lui Kolmogorov
Desigur, atunci când se calculează funcția de distribuție cumulativă, ar trebui să se folosească relația menționată între distribuțiile binomiale și beta. Această metodă este cu siguranță mai bună decât însumarea directă atunci când n > 10.
În manualele clasice de statistică, pentru a obține valorile distribuției binomiale, se recomandă adesea utilizarea formulelor bazate pe teoreme limită (cum ar fi formula Moivre-Laplace). Trebuie remarcat faptul că din punct de vedere pur computaţional valoarea acestor teoreme este aproape de zero, mai ales acum, când există un computer puternic pe aproape fiecare masă. Principalul dezavantaj al aproximărilor de mai sus este acuratețea lor complet insuficientă pentru valorile lui n tipice pentru majoritatea aplicațiilor. Un dezavantaj nu mai mic este absența oricăror recomandări clare cu privire la aplicabilitatea uneia sau alteia aproximări (în textele standard sunt date doar formulări asimptotice, nu sunt însoțite de estimări de acuratețe și, prin urmare, sunt de puțin folos). Aș spune că ambele formule sunt valabile doar pentru n< 200 и для совсем грубых, ориентировочных расчетов, причем делаемых “вручную” с помощью статистических таблиц. А вот связь между биномиальным распределением и бета-распределением позволяет вычислять биномиальное распределение достаточно экономно.
Nu iau în considerare aici problema găsirii cuantilelor: pentru distribuțiile discrete, este banală, iar în acele probleme în care apar astfel de distribuții, ea, de regulă, nu este relevantă. Dacă mai sunt necesare cuantile, recomand reformularea problemei în așa fel încât să se lucreze cu valorile p (semnificații observate). Iată un exemplu: la implementarea unor algoritmi de enumerare, la fiecare pas este necesară verificarea ipoteza statistica despre o variabilă aleatoare binomială. Conform abordării clasice, la fiecare pas este necesar să se calculeze statisticile criteriului și să se compare valoarea acestuia cu limita mulțimii critice. Deoarece, totuși, algoritmul este enumerativ, este necesar să se determine din nou granița setului critic de fiecare dată (la urma urmei, dimensiunea eșantionului se schimbă de la pas la pas), ceea ce crește neproductiv costurile de timp. Abordare modernă recomandă calcularea semnificației observate și compararea acesteia cu nivel de încredere, economisind la căutarea cuantilelor.
Prin urmare, următoarele coduri nu calculează funcția inversă, în schimb, este dată funcția rev_binomialDF, care calculează probabilitatea p de succes într-o singură încercare având în vedere numărul n de încercări, numărul m de succese din acestea și valoarea y a probabilității de a obține aceste m succese. Aceasta folosește relația menționată mai sus dintre distribuțiile binomiale și beta.
De fapt, această funcție vă permite să obțineți limitele intervalelor de încredere. Într-adevăr, să presupunem că obținem m succese în n încercări binomiale. După cum se știe, limita din stânga a intervalului de încredere cu două fețe pentru parametrul p cu un nivel de încredere este 0 dacă m = 0 și for este soluția ecuației  . În mod similar, limita dreaptă este 1 dacă m = n și pentru este o soluție a ecuației
. În mod similar, limita dreaptă este 1 dacă m = n și pentru este o soluție a ecuației  . Aceasta implică faptul că pentru a găsi limita stângă, trebuie să rezolvăm ecuația
. Aceasta implică faptul că pentru a găsi limita stângă, trebuie să rezolvăm ecuația  , și pentru a căuta cea potrivită - ecuația
, și pentru a căuta cea potrivită - ecuația  . Acestea sunt rezolvate în funcțiile binom_leftCI și binom_rightCI , care returnează limitele superioare și, respectiv, inferioare ale intervalului de încredere cu două fețe.
. Acestea sunt rezolvate în funcțiile binom_leftCI și binom_rightCI , care returnează limitele superioare și, respectiv, inferioare ale intervalului de încredere cu două fețe.
Vreau să observ că, dacă nu este necesară o precizie absolut incredibilă, atunci pentru n suficient de mare, puteți utiliza următoarea aproximare [B.L. van der Waerden, Statistica matematică. M: IL, 1960, cap. 2, sec. 7]:  , unde g este cuantila distribuției normale. Valoarea acestei aproximări este că există aproximări foarte simple care vă permit să calculați cuantilele distribuției normale (vezi textul despre calcularea distribuției normale și secțiunea corespunzătoare a acestei referințe). În practica mea (în principal pentru n > 100), această aproximare a dat aproximativ 3-4 cifre, ceea ce, de regulă, este destul de suficient.
, unde g este cuantila distribuției normale. Valoarea acestei aproximări este că există aproximări foarte simple care vă permit să calculați cuantilele distribuției normale (vezi textul despre calcularea distribuției normale și secțiunea corespunzătoare a acestei referințe). În practica mea (în principal pentru n > 100), această aproximare a dat aproximativ 3-4 cifre, ceea ce, de regulă, este destul de suficient.
Calculele cu următoarele coduri necesită fișierele betaDF.h , betaDF.cpp (vezi secțiunea despre distribuția beta), precum și logGamma.h , logGamma.cpp (vezi anexa A). De asemenea, puteți vedea un exemplu de utilizare a funcțiilor.
fișier binomialDF.h
| #ifndef __BINOMIAL_H__ #include "betaDF.h" binom dubluDF(încercări duble, succese duble, p dublu); /* * Să fie „încercări” de observații independente * cu probabilitatea „p” de succes în fiecare. * Calculați probabilitatea B(reușite|încercări,p) ca numărul * de succese să fie între 0 și „reușite” (inclusiv). */ double rev_binomialDF(încercări duble, succese duble, y dublu); /* * Fie cunoscută probabilitatea y de cel puțin m succese * în încercările schemei Bernoulli. Funcția găsește probabilitatea p * de succes într-o singură încercare. * * Următoarea relație este utilizată în calcule * * 1 - p = rev_Beta(încercări-reușite| succese+1, y). */ double binom_leftCI(double trials, double success, double level); /* Să fie „încercări” de observații independente * cu probabilitatea „p” de succes în fiecare * iar numărul de succese este „reușite”. * Limita stângă a intervalului de încredere cu două fețe * este calculată cu nivelul nivelului de semnificație. */ double binom_rightCI(double n, double succeses, double level); /* Să fie „încercări” de observații independente * cu probabilitatea „p” de succes în fiecare * iar numărul de succese este „reușite”. * Limita dreaptă a intervalului de încredere cu două fețe * este calculată cu nivelul nivelului de semnificație. */ #endif /* Se termină #ifndef __BINOMIAL_H__ */ |
fișier binomialDF.cpp
| /************************************************ **** **********/ /* Distribuție binomială */ /**************************** **** ****************************/ #include |
Salutări tuturor cititorilor!
Analiza statistică, după cum știți, se ocupă de colectarea și prelucrarea datelor reale. Este util, și adesea profitabil, pentru că. concluziile corecte vă permit să evitați greșelile și pierderile în viitor și, uneori, să ghiciți corect acest viitor. Datele colectate reflectă starea unor fenomene observate. Datele sunt adesea (dar nu întotdeauna) numerice și pot fi manipulate cu diverse manipulări matematice pentru a extrage informații suplimentare.
Cu toate acestea, nu toate fenomenele sunt măsurate pe o scară cantitativă precum 1, 2, 3 ... 100500 ... Nu întotdeauna un fenomen poate lua un infinit sau un număr mare de stări diferite. De exemplu, genul unei persoane poate fi fie M, fie F. trăgătorul fie lovește ținta, fie ratează. Puteți vota fie „pentru”, fie „împotrivă”, etc. și așa mai departe. Cu alte cuvinte, astfel de date reflectă starea unui atribut alternativ - fie „da” (evenimentul a avut loc), fie „nu” (evenimentul nu a avut loc). Evenimentul care urmează (rezultat pozitiv) se mai numește și „succes”. Astfel de fenomene pot fi, de asemenea, masive și întâmplătoare. Prin urmare, ele pot fi măsurate și se pot trage concluzii valide statistic.
Se numesc experimente cu astfel de date Schema Bernoulli, în onoarea celebrului matematician elvețian care a stabilit că atunci când în număr mare studii, raportul dintre rezultatele pozitive și numărul total de încercări tinde la probabilitatea ca acest eveniment să apară.
Variabilă alternativă de caracteristică
Pentru a utiliza aparatul matematic în analiză, rezultatele acestor observații trebuie notate în formă numerică. Pentru a face acest lucru, unui rezultat pozitiv i se atribuie numărul 1, unul negativ - 0. Cu alte cuvinte, avem de-a face cu o variabilă care poate lua doar două valori: 0 sau 1.
Ce beneficii se poate obține din asta? De fapt, nu mai puțin decât din date obișnuite. Deci, este ușor să numărăm numărul de rezultate pozitive - este suficient să însumăm toate valorile, de exemplu. toate 1 (succes). Puteți merge mai departe, dar pentru aceasta trebuie să introduceți câteva notații.
Primul lucru de remarcat este că rezultatele pozitive (care sunt egale cu 1) au o anumită probabilitate de a apărea. De exemplu, obținerea capetelor la aruncarea unei monede este ½ sau 0,5. Această probabilitate este indicată în mod tradițional Literă latină p. Prin urmare, probabilitatea ca un eveniment alternativ să se producă este 1-p, care se notează și prin q, acesta este q = 1 – p. Aceste denumiri pot fi sistematizate vizual sub forma unei plăci de distribuție variabilă X.
Acum avem o listă de valori posibile și probabilitățile acestora. Puteți începe să calculați astfel de caracteristici minunate ale unei variabile aleatorii ca valorea estimataȘi dispersie. Permiteți-mi să vă reamintesc că așteptarea matematică este calculată ca suma produselor tuturor valorilor posibile și probabilitățile lor corespunzătoare:
![]()
Să calculăm valoarea așteptată folosind notația din tabelele de mai sus.
Se pare că așteptarea matematică a unui semn alternativ este egală cu probabilitatea acestui eveniment - p.
Acum să definim care este varianța unei caracteristici alternative. Permiteți-mi să vă reamintesc, de asemenea, că varianța este pătratul mediu al abaterilor de la așteptarea matematică. Formula generala(pentru date discrete) are forma:
De aici variația caracteristicii alternative:

Este ușor de observat că această dispersie are un maxim de 0,25 (at p=0,5).
Abaterea standard - rădăcina varianței:
Valoarea maximă nu depășește 0,5.
După cum puteți vedea, atât așteptarea matematică, cât și varianța semnului alternativ au o formă foarte compactă.
Distribuția binomială a unei variabile aleatoare
Acum luați în considerare situația dintr-un unghi diferit. Într-adevăr, cui îi pasă că pierderea medie de capete la o aruncare este de 0,5? Este chiar imposibil de imaginat. Este mai interesant să ridicăm problema numărului de capete care apar pentru un anumit număr de aruncări.
Cu alte cuvinte, cercetătorul este adesea interesat de probabilitatea ca un anumit număr de evenimente de succes să aibă loc. Acesta poate fi numărul de produse defecte din lotul testat (1 - defect, 0 - bun) sau numărul de recuperări (1 - sănătos, 0 - bolnav), etc. Numărul de astfel de „reușite” va fi egal cu suma tuturor valorilor variabilei X, adică numărul de rezultate unice.
Valoare aleatoare B se numește binom și ia valori de la 0 la n(la B= 0 - toate părțile sunt bune, cu B = n- toate piesele sunt defecte). Se presupune că toate valorile X independente unele de altele. Luați în considerare principalele caracteristici ale variabilei binomiale, adică vom stabili așteptările matematice, varianța și distribuția acesteia.
Așteptarea unei variabile binomiale este foarte ușor de obținut. Amintiți-vă că există o sumă de așteptări matematice pentru fiecare valoare adăugată și este aceeași pentru toată lumea, prin urmare:
De exemplu, așteptarea numărului de capete la 100 de aruncări este 100 × 0,5 = 50.
Acum derivăm formula pentru varianța variabilei binomiale. este suma varianțelor. De aici
Abaterea standard, respectiv
Pentru 100 de aruncări de monede, abaterea standard este
Și, în sfârșit, luați în considerare distribuția valoare binomială, adică probabilitatea ca variabila aleatoare B va lua diverse sensuri k, Unde 0≤k≤n. Pentru o monedă, această problemă ar putea suna așa: care este probabilitatea de a obține 40 de capete în 100 de aruncări?
Pentru a înțelege metoda de calcul, să ne imaginăm că moneda este aruncată doar de 4 ori. Oricare parte poate cădea de fiecare dată. Ne întrebăm: care este probabilitatea de a obține 2 capete din 4 aruncări. Fiecare aruncare este independentă una de cealaltă. Aceasta înseamnă că probabilitatea de a obține orice combinație va fi egală cu produsul dintre probabilitățile unui rezultat dat pentru fiecare aruncare individuală. Fie O capete și P cozi. Atunci, de exemplu, una dintre combinațiile care ni se potrivesc poate arăta ca OOPP, adică:

Probabilitatea unei astfel de combinații este egală cu produsul a două probabilități de a obține cap și a încă două probabilități de a nu apărea (evenimentul invers calculat ca 1-p), adică 0,5×0,5×(1-0,5)×(1-0,5)=0,0625. Aceasta este probabilitatea uneia dintre combinațiile care ni se potrivesc. Dar întrebarea era despre numărul total de vulturi, și nu despre o anumită ordine. Apoi trebuie să adăugați probabilitățile tuturor combinațiilor în care există exact 2 vulturi. Este clar că toate sunt la fel (produsul nu se schimbă de la schimbarea locurilor factorilor). Prin urmare, trebuie să calculați numărul lor și apoi să înmulțiți cu probabilitatea unei astfel de combinații. Să numărăm toate combinațiile de 4 aruncări a 2 vulturi: RROO, RORO, ROOR, ORRO, OROR, OORR. Doar 6 variante.

Prin urmare, probabilitatea dorită de a obține 2 capete după 4 aruncări este 6×0,0625=0,375.
Cu toate acestea, numărarea în acest fel este plictisitoare. Deja pentru 10 monede, va fi foarte dificil să obțineți numărul total de opțiuni prin forță brută. Prin urmare, oamenii inteligenți au inventat cu mult timp în urmă o formulă, cu ajutorul căreia calculează numărul de combinații diferite de n elemente prin k, Unde n este numărul total de elemente, k este numărul de elemente ale căror opțiuni de aranjare sunt calculate. Formula combinată a n elemente prin k este:
![]()
Lucruri similare au loc în secțiunea de combinatorie. Trimit acolo pe toți cei care doresc să-și îmbunătățească cunoștințele. De aici, apropo, numele distribuției binomiale (formula de mai sus este coeficientul de expansiune al binomului Newton).
Formula pentru determinarea probabilității poate fi generalizată cu ușurință la orice număr nȘi k. Ca rezultat, formula de distribuție binomială are următoarea formă.
Cu alte cuvinte: înmulțiți numărul de combinații potrivite cu probabilitatea uneia dintre ele.
Pentru uz practic este suficient doar să cunoaștem formula distribuției binomiale. Și poate nici nu știți - mai jos este cum să determinați probabilitatea folosind Excel. Dar e mai bine să știi.
Să folosim această formulă pentru a calcula probabilitatea de a obține 40 de capete în 100 de aruncări:
Sau doar 1,08%. Pentru comparație, probabilitatea așteptării matematice a acestui experiment, adică 50 de capete, este de 7,96%. Probabilitatea maximă a unei valori binomiale aparține valorii corespunzătoare așteptării matematice.
Calcularea probabilităților de distribuție binomială în Excel
Dacă utilizați doar hârtie și un calculator, atunci calcule folosind formula distribuție binomială, în ciuda absenței integralelor, sunt destul de dificile. De exemplu, o valoare de 100! - are mai mult de 150 de caractere. Este imposibil să calculați acest lucru manual. Anterior, și chiar acum, se foloseau formule aproximative pentru a calcula astfel de cantități. În acest moment, este recomandabil să folosiți software special, precum MS Excel. Astfel, orice utilizator (chiar și un umanist de educație) poate calcula cu ușurință probabilitatea valorii unei variabile aleatoare distribuite binomial.
Pentru a consolida materialul, vom folosi Excel deocamdată ca un calculator obișnuit, adică. Să facem un calcul pas cu pas folosind formula de distribuție binomială. Să calculăm, de exemplu, probabilitatea de a obține 50 de capete. Mai jos este o poză cu pașii de calcul și rezultatul final.

După cum puteți vedea, rezultatele intermediare sunt de o asemenea scară încât nu se potrivesc într-o celulă, deși funcții simple de tipul sunt folosite peste tot: FACTOR (calcul factorial), POWER (ridicarea unui număr la o putere), precum și ca operatori de înmulţire şi împărţire. Mai mult, acest calcul este destul de greoi, în orice caz nu este compact, deoarece multe celule implicate. Și da, este greu să-ți dai seama.
În general, Excel oferă o funcție gata făcută pentru calcularea probabilităților distribuției binomiale. Funcția se numește BINOM.DIST.

Numărul de succese este numărul de încercări reușite. Avem 50 dintre ele.
Numărul de încercări- număr de aruncări: de 100 de ori.
Probabilitatea de succes– probabilitatea de a obține capete la o aruncare este de 0,5.
Integral- este indicat fie 1, fie 0. Dacă 0, atunci probabilitatea este calculată P(B=k); dacă 1, atunci se calculează funcția de distribuție binomială, i.e. suma tuturor probabilităților de la B=0 inainte de B=k inclusiv.
Apăsăm OK și obținem același rezultat ca mai sus, doar totul a fost calculat de o singură funcție.

Foarte confortabil. De dragul experimentului, în loc de ultimul parametru 0, punem 1. Obținem 0,5398. Aceasta înseamnă că în 100 de aruncări de monede, probabilitatea de a obține capete între 0 și 50 este de aproape 54%. Și la început părea că ar trebui să fie de 50%. În general, calculele se fac ușor și rapid.
Un analist adevărat trebuie să înțeleagă cum se comportă funcția (care este distribuția ei), așa că haideți să calculăm probabilitățile pentru toate valorile de la 0 la 100. Adică să ne întrebăm: care este probabilitatea ca niciun vultur să nu cadă, că va cădea 1 vultur, 2, 3, 50, 90 sau 100. Calculul este prezentat în următoarea imagine în mișcare. Linia albastră este distribuția binomială în sine, punctul roșu este probabilitatea pentru un anumit număr de succese k.

S-ar putea întreba, nu este distribuția binomială similară cu... Da, foarte asemănătoare. Chiar și De Moivre (în 1733) spunea că cu eșantioane mari se apropie distribuția binomială (nu știu cum se numea atunci), dar nimeni nu l-a ascultat. Doar Gauss, și apoi Laplace, 60-70 de ani mai târziu, au redescoperit și studiat cu atenție legea distribuției normale. Graficul de mai sus arată clar că probabilitatea maximă cade pe așteptarea matematică și, pe măsură ce se abate de la aceasta, scade brusc. La fel ca legea normală.
Distribuția binomială este de mare importanță practică, apare destul de des. Prin utilizarea calcule Excel realizat rapid si usor. Așa că nu ezitați să-l utilizați.
În acest sens îmi propun să-mi iau rămas bun până la următoarea întâlnire. Toate cele bune, fiți sănătoși!




