"ส่วนแรกกำหนดข้อกำหนดที่จำเป็นขั้นต่ำสำหรับการทำความเข้าใจเคมีเคมี และส่วนที่สองประกอบด้วยข้อเท็จจริงที่คุณจำเป็นต้องรู้เพื่อความเข้าใจที่ลึกซึ้งยิ่งขึ้นเกี่ยวกับวิธีการวิเคราะห์หลายตัวแปร การนำเสนอนี้แสดงตัวอย่างพร้อมตัวอย่างที่ทำไว้ในสมุดงาน Excel Matrix.xlsที่มาพร้อมกับเอกสารนี้

ลิงก์ไปยังตัวอย่างจะอยู่ในข้อความเป็นวัตถุ Excel ตัวอย่างเหล่านี้มีลักษณะเป็นนามธรรม ไม่ได้เชื่อมโยงกับงานแต่อย่างใด เคมีวิเคราะห์. ตัวอย่างจริงการใช้พีชคณิตเมทริกซ์ในเคมีเคมีจะกล่าวถึงในบทความอื่นๆ ที่ครอบคลุมการใช้งานทางเคมีที่หลากหลาย

การวัดส่วนใหญ่ที่ทำในเคมีวิเคราะห์ไม่ใช่การวัดโดยตรง ทางอ้อม- ซึ่งหมายความว่าในการทดลอง แทนที่จะได้ค่าของสารวิเคราะห์ C ที่ต้องการ (ความเข้มข้น) จะได้รับค่าอื่น x(สัญญาณ) เกี่ยวข้องแต่ไม่เท่ากับ C เช่น x(C) ≠ C. ตามกฎแล้วประเภทของการพึ่งพา x(C) ไม่เป็นที่รู้จัก แต่โชคดีในเคมีวิเคราะห์ การวัดส่วนใหญ่เป็นสัดส่วน ซึ่งหมายความว่าเมื่อความเข้มข้นของ C เพิ่มขึ้น กเท่า สัญญาณ X จะเพิ่มขึ้นตามจำนวนที่เท่ากัน นั่นคือ x(กค) = เอ็กซ์(ค) นอกจากนี้ สัญญาณยังเป็นการบวก ดังนั้นสัญญาณจากตัวอย่างซึ่งมีสารสองชนิดที่มีความเข้มข้น C 1 และ C 2 อยู่จะเท่ากับผลรวมของสัญญาณจากแต่ละส่วนประกอบ กล่าวคือ x(ค 1 + ค 2) = x(ค1)+ x(ค2). สัดส่วนและส่วนเสริมร่วมกันให้ ความเป็นเส้นตรง- สามารถยกตัวอย่างได้มากมายเพื่ออธิบายหลักการของความเป็นเชิงเส้น แต่ก็เพียงพอที่จะกล่าวถึงตัวอย่างที่โดดเด่นที่สุดสองตัวอย่าง ได้แก่ โครมาโตกราฟีและสเปกโทรสโกปี คุณลักษณะที่สองที่มีอยู่ในการทดลองทางเคมีวิเคราะห์คือ หลายช่อง- อุปกรณ์วิเคราะห์ที่ทันสมัยจะวัดสัญญาณหลายช่องพร้อมกัน ตัวอย่างเช่น ความเข้มของการส่งผ่านแสงจะถูกวัดสำหรับความยาวคลื่นหลายช่วงในคราวเดียว กล่าวคือ สเปกตรัม ดังนั้นในการทดลองเราจึงต้องจัดการกับสัญญาณต่างๆ มากมาย x 1 , x 2 ,...., x n กำหนดลักษณะชุดความเข้มข้น C 1 , C 2 , ..., C m ของสารที่มีอยู่ในระบบที่กำลังศึกษา

ข้าว. 1 สเปกตรัม

ดังนั้น การทดลองเชิงวิเคราะห์จึงมีลักษณะเป็นเส้นตรงและหลายมิติ ดังนั้นจึงสะดวกที่จะพิจารณาข้อมูลการทดลองเป็นเวกเตอร์และเมทริกซ์ และจัดการข้อมูลเหล่านั้นโดยใช้เครื่องมือของพีชคณิตเมทริกซ์ ประสิทธิผลของแนวทางนี้แสดงไว้ในตัวอย่างที่แสดงใน ซึ่งนำเสนอสเปกตรัม 3 สเปกตรัมที่ถ่ายที่ความยาวคลื่น 200 ช่วงตั้งแต่ 4000 ถึง 4796 ซม. -1 อันดับแรก ( x 1) และวินาที ( x 2) ได้รับสเปกตรัมสำหรับตัวอย่างมาตรฐานซึ่งทราบความเข้มข้นของสาร A และ B สองชนิด: ในตัวอย่างแรก [A] = 0.5, [B] = 0.1 และในตัวอย่างที่สอง [A] = 0.2, [ ข] = 0.6 สิ่งที่สามารถพูดได้เกี่ยวกับตัวอย่างใหม่ที่ไม่รู้จักซึ่งมีการระบุสเปกตรัม x 3 ?

ให้เราพิจารณาสเปกตรัมทดลองสามสเปกตรัม x 1 , x 2 และ x 3 เป็นเวกเตอร์สามมิติที่มีมิติ 200 การใช้พีชคณิตเชิงเส้น เราสามารถแสดงได้อย่างง่ายดาย x 3 = 0.1 x 1 +0.3 x 2 ดังนั้นตัวอย่างที่สามมีเพียงสาร A และ B เท่านั้นที่มีความเข้มข้น [A] = 0.5×0.1 + 0.2×0.3 = 0.11 และ [B] = 0.1×0.1 + 0.6×0.3 = 0.19

1. ข้อมูลพื้นฐาน

1.1 เมทริกซ์

เมทริกซ์เรียกว่าตารางตัวเลขสี่เหลี่ยม เป็นต้น

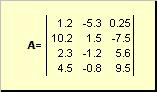
ข้าว. 2 เมทริกซ์

เมทริกซ์แสดงด้วยอักษรตัวพิมพ์ใหญ่ ( ก) และองค์ประกอบ - โดยตัวอักษรพิมพ์เล็กที่สอดคล้องกันพร้อมดัชนีเช่น กฉัน ดัชนีแรกระบุแถวและดัชนีที่สองคือคอลัมน์ ในเคมีเคมี เป็นเรื่องปกติที่จะต้องระบุค่าสูงสุดของดัชนีด้วยตัวอักษรเดียวกับตัวดัชนี แต่ใช้อักษรตัวพิมพ์ใหญ่ ดังนั้นเมทริกซ์ กยังสามารถเขียนเป็น ( ก ฉัน , ฉัน = 1,..., ฉัน; เจ = 1,..., เจ- สำหรับเมทริกซ์ตัวอย่าง ฉัน = 4, เจ= 3 และ ก 23 = −7.5.

คู่ของตัวเลข ฉันและ เจเรียกว่ามิติของเมทริกซ์และเขียนแทนเป็น ฉัน× เจ- ตัวอย่างของเมทริกซ์ในเคมีเคมีคือชุดสเปกตรัมที่ได้รับ ฉันตัวอย่างสำหรับ เจความยาวคลื่น

1.2. การดำเนินการที่ง่ายที่สุดด้วยเมทริกซ์

เมทริกซ์สามารถเป็นได้ คูณด้วยตัวเลข- ในกรณีนี้ แต่ละองค์ประกอบจะคูณด้วยตัวเลขนี้ ตัวอย่างเช่น -

ข้าว. 3 การคูณเมทริกซ์ด้วยตัวเลข

เมทริกซ์สองตัวที่มีมิติเดียวกันสามารถแยกเป็นองค์ประกอบได้ พับและ ลบ- ตัวอย่างเช่น,

ข้าว. 4 การบวกเมทริกซ์

จากการคูณด้วยตัวเลขและการบวกจะได้เมทริกซ์ที่มีมิติเดียวกัน

เมทริกซ์ศูนย์คือเมทริกซ์ที่ประกอบด้วยศูนย์ มันถูกกำหนดไว้ โอ- เห็นได้ชัดว่า ก+โอ = ก, ก−ก = โอและ 0 ก = โอ.

เมทริกซ์สามารถเป็นได้ ย้าย- ในระหว่างการดำเนินการนี้เมทริกซ์จะถูกพลิกเช่น แถวและคอลัมน์ถูกสลับกัน การขนย้ายถูกระบุด้วยจำนวนเฉพาะ ก"หรือดัชนี กที ดังนั้นหาก ก = {ก ฉัน , ฉัน = 1,..., ฉัน; เจ = 1,...,เจ), ที่ กเสื้อ = ( ก จิ , เจ = 1,...,เจ- ผม = 1,..., ฉัน- ตัวอย่างเช่น

ข้าว. 5 การขนย้ายเมทริกซ์

เห็นได้ชัดว่า ( กเสื้อ) เสื้อ = ก, (ก+บี) ที =กที+ บีที

1.3. การคูณเมทริกซ์

เมทริกซ์สามารถเป็นได้ คูณแต่เฉพาะในกรณีที่มีขนาดที่เหมาะสมเท่านั้น เหตุใดจึงเป็นเช่นนี้จะชัดเจนจากคำจำกัดความ ผลิตภัณฑ์เมทริกซ์ ก, มิติ ฉัน× เคและเมทริกซ์ บี, มิติ เค× เจเรียกว่าเมทริกซ์ ค, มิติ ฉัน× เจซึ่งมีองค์ประกอบเป็นตัวเลข

ดังนั้นสำหรับผลิตภัณฑ์ เอบีจำเป็นที่จำนวนคอลัมน์ในเมทริกซ์ด้านซ้าย กเท่ากับจำนวนแถวในเมทริกซ์ด้านขวา บี- ตัวอย่างของผลิตภัณฑ์เมทริกซ์ -

รูปที่ 6 ผลคูณของเมทริกซ์

กฎสำหรับการคูณเมทริกซ์สามารถกำหนดได้ดังนี้ เพื่อค้นหาองค์ประกอบเมทริกซ์ ค, ยืนอยู่ที่ทางแยก ฉัน-บรรทัดที่ และ เจคอลัมน์ที่ ( ค ฉัน) จะต้องคูณองค์ประกอบด้วยองค์ประกอบ ฉัน- แถวที่หนึ่งของเมทริกซ์แรก กบน เจคอลัมน์ที่ th ของเมทริกซ์ตัวที่สอง บีและบวกผลลัพธ์ทั้งหมดเข้าด้วยกัน ในตัวอย่างที่แสดง องค์ประกอบจากแถวที่สามและคอลัมน์ที่สองจะได้มาเป็นผลรวมของผลคูณเชิงองค์ประกอบของแถวที่สาม กและคอลัมน์ที่สอง บี

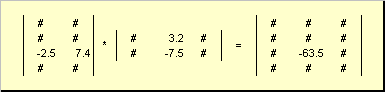
รูปที่ 7 องค์ประกอบของผลคูณของเมทริกซ์

ผลคูณของเมทริกซ์ขึ้นอยู่กับลำดับเช่น เอบี ≠ ปริญญาตรีอย่างน้อยก็ด้วยเหตุผลด้านมิติ พวกเขาบอกว่ามันไม่สับเปลี่ยน อย่างไรก็ตาม ผลคูณของเมทริกซ์มีความเชื่อมโยง นี่หมายความว่า เอบีซี = (เอบี)ค = ก(บี.ซี.- นอกจากนี้ยังเป็นการจำหน่ายเช่น ก(บี+ค) = เอบี+เอ.ซี.- เห็นได้ชัดว่า อ.โอ. = โอ.

1.4. เมทริกซ์จตุรัส

หากจำนวนคอลัมน์เมทริกซ์เท่ากับจำนวนแถว ( ฉัน = เจ=น) จากนั้นเมทริกซ์ดังกล่าวเรียกว่าสี่เหลี่ยมจัตุรัส ในส่วนนี้เราจะพิจารณาเฉพาะเมทริกซ์ดังกล่าวเท่านั้น ในบรรดาเมทริกซ์เหล่านี้ สามารถแยกแยะเมทริกซ์ที่มีคุณสมบัติพิเศษได้

เดี่ยวเมทริกซ์ (แสดง ฉัน,และบางครั้ง อี) เป็นเมทริกซ์ที่องค์ประกอบทั้งหมดมีค่าเท่ากับศูนย์ ยกเว้นองค์ประกอบในแนวทแยงซึ่งมีค่าเท่ากับ 1 นั่นคือ

อย่างชัดเจน AI. = ไอเอ = ก.

เมทริกซ์เรียกว่า เส้นทแยงมุมถ้าองค์ประกอบทั้งหมดยกเว้นเส้นทแยงมุม ( ก ครั้งที่สอง) เท่ากับศูนย์ ตัวอย่างเช่น

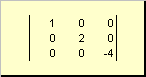
ข้าว. 8 เมทริกซ์แนวทแยง

เมทริกซ์ กเรียกว่าด้านบน สามเหลี่ยมหากองค์ประกอบทั้งหมดที่อยู่ต่ำกว่าเส้นทแยงมุมมีค่าเท่ากับศูนย์ เช่น ก ฉัน= 0 ณ ฉัน>เจ- ตัวอย่างเช่น

ข้าว. 9 เมทริกซ์สามเหลี่ยมบน

เมทริกซ์สามเหลี่ยมด้านล่างถูกกำหนดในทำนองเดียวกัน

เมทริกซ์ กเรียกว่า สมมาตร, ถ้า กเสื้อ = ก- กล่าวอีกนัยหนึ่ง ก ฉัน = ก จิ- ตัวอย่างเช่น

ข้าว. 10 เมทริกซ์สมมาตร

เมทริกซ์ กเรียกว่า ตั้งฉาก, ถ้า

กที ก = เอเอเสื้อ = ฉัน.

เมทริกซ์เรียกว่า ปกติถ้า

1.5. ติดตามและปัจจัยกำหนด

ต่อไปเมทริกซ์จตุรัส ก(แสดงโดย Tr( ก) หรือ Sp( ก)) คือผลรวมขององค์ประกอบในแนวทแยง

ตัวอย่างเช่น,

ข้าว. 11 การติดตามเมทริกซ์

เห็นได้ชัดว่า

เอสพี(α ก) = α เอสพี( ก) และ

เอสพี( ก+บี) = เอสพี( ก)+ เอสพี( บี).

ก็สามารถแสดงได้ว่า

เอสพี( ก) = เอสพี( กเสื้อ), Sp( ฉัน) = เอ็น,

และนั่นด้วย

เอสพี( เอบี) = เอสพี( ปริญญาตรี).

ลักษณะสำคัญอีกประการหนึ่งของเมทริกซ์จตุรัสก็คือ ปัจจัยกำหนด(หมายถึง det( ก- คำจำกัดความของปัจจัยกำหนดใน กรณีทั่วไปค่อนข้างซับซ้อนดังนั้นเราจะเริ่มต้นด้วยตัวเลือกที่ง่ายที่สุด - เมทริกซ์ กขนาด (2×2) แล้ว

สำหรับเมทริกซ์ (3×3) ดีเทอร์มิแนนต์จะเท่ากับ

ในกรณีของเมทริกซ์ ( เอ็น× เอ็น) ดีเทอร์มิแนนต์จะคำนวณเป็นผลรวม 1·2·3· ... · เอ็น= เอ็น- เงื่อนไขซึ่งแต่ละข้อจะเท่ากัน

ดัชนี เค 1 , เค 2 ,..., เคเอ็นถูกกำหนดเป็นการเรียงสับเปลี่ยนลำดับที่เป็นไปได้ทั้งหมด รตัวเลขในชุด (1, 2, ..., เอ็น- การคำนวณดีเทอร์มิแนนต์ของเมทริกซ์เป็นขั้นตอนที่ซับซ้อนซึ่งในทางปฏิบัติจะดำเนินการโดยใช้โปรแกรมพิเศษ ตัวอย่างเช่น,

ข้าว. 12 ดีเทอร์มิแนนต์เมทริกซ์

ให้เราสังเกตเฉพาะคุณสมบัติที่ชัดเจนเท่านั้น:

เดต( ฉัน) = 1, เดช( ก) = เดช( กเสื้อ)

เดต( เอบี) = เดช( ก)เดต( บี).

1.6. เวกเตอร์

หากเมทริกซ์ประกอบด้วยคอลัมน์เดียวเท่านั้น ( เจ= 1) จากนั้นจึงเรียกวัตถุดังกล่าว เวกเตอร์- แม่นยำยิ่งขึ้นคือเวกเตอร์คอลัมน์ ตัวอย่างเช่น

เราสามารถพิจารณาเมทริกซ์ที่ประกอบด้วยหนึ่งแถวได้เช่นกัน

วัตถุนี้ก็เป็นเวกเตอร์เช่นกัน แต่ เวกเตอร์แถว- เมื่อวิเคราะห์ข้อมูล สิ่งสำคัญคือต้องเข้าใจว่าเรากำลังจัดการกับเวกเตอร์ใด - คอลัมน์หรือแถว ดังนั้นสเปกตรัมที่ใช้สำหรับหนึ่งตัวอย่างจึงถือเป็นเวกเตอร์แถวได้ จากนั้น เซตของความเข้มสเปกตรัมที่ความยาวคลื่นที่แน่นอนสำหรับตัวอย่างทั้งหมดควรถือเป็นเวกเตอร์คอลัมน์

มิติของเวกเตอร์คือจำนวนองค์ประกอบ

เห็นได้ชัดว่าเวกเตอร์คอลัมน์ใดๆ สามารถแปลงเป็นเวกเตอร์แถวได้โดยการขนย้าย กล่าวคือ

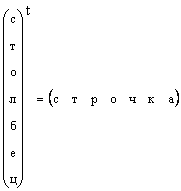
ในกรณีที่รูปร่างของเวกเตอร์ไม่ได้ระบุไว้เป็นพิเศษ แต่พูดง่ายๆ ว่าเป็นเวกเตอร์ ก็จะหมายถึงเวกเตอร์คอลัมน์ เราจะปฏิบัติตามกฎนี้ด้วย เวกเตอร์แสดงด้วยตัวอักษรพิมพ์เล็ก ตั้งตรง และหนา เวกเตอร์ศูนย์คือเวกเตอร์ที่มีองค์ประกอบทั้งหมดเป็นศูนย์ มันถูกกำหนดไว้ 0 .

1.7. การดำเนินการที่ง่ายที่สุดด้วยเวกเตอร์

เวกเตอร์สามารถบวกและคูณด้วยตัวเลขได้ในลักษณะเดียวกับเมทริกซ์ ตัวอย่างเช่น,

ข้าว. 13 การดำเนินการกับเวกเตอร์

เวกเตอร์สองตัว xและ ยถูกเรียก โคลิเนียร์ถ้ามีเลข α แบบนั้น

1.8. ผลิตภัณฑ์ของเวกเตอร์

เวกเตอร์สองตัวที่มีมิติเท่ากัน เอ็นสามารถคูณได้ ให้มีเวกเตอร์สองตัว x = (x 1 , x 2 ,...,xน)ที และ ย = (ย 1 , ย 2 ,...,ยน) เสื้อ จากกฎการคูณแบบแถวต่อคอลัมน์ เราสามารถเขียนผลคูณสองจากกฎเหล่านี้ได้: xที ยและ เอ็กซ์ซีที งานแรก

เรียกว่า สเกลาร์หรือ ภายใน- ผลลัพธ์ของมันคือตัวเลข นอกจากนี้ยังแสดงด้วย ( x,ย)= xที ย- ตัวอย่างเช่น,

ข้าว. 14 ผลคูณภายใน (สเกลาร์)

ชิ้นที่สอง

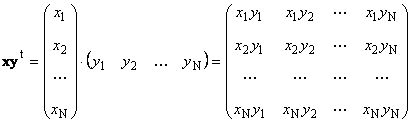
เรียกว่า ภายนอก- ผลลัพธ์ของมันคือเมทริกซ์ของมิติ ( เอ็น× เอ็น- ตัวอย่างเช่น,

ข้าว. 15 งานภายนอก

เวกเตอร์ที่มีผลคูณสเกลาร์เป็นศูนย์จะถูกเรียกว่า ตั้งฉาก.

1.9. บรรทัดฐานของเวกเตอร์

ผลคูณสเกลาร์ของเวกเตอร์ที่มีตัวมันเองเรียกว่ากำลังสองสเกลาร์ ค่านี้

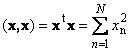
กำหนดสี่เหลี่ยมจัตุรัส ความยาวเวกเตอร์ x- เพื่อระบุความยาว (หรือที่เรียกว่า บรรทัดฐานเวกเตอร์) ใช้สัญลักษณ์

ตัวอย่างเช่น,

ข้าว. 16 บรรทัดฐานเวกเตอร์

เวกเตอร์ความยาวหน่วย (|| x- = 1) เรียกว่าทำให้เป็นมาตรฐาน เวกเตอร์ที่ไม่ใช่ศูนย์ ( x ≠ 0 ) สามารถทำให้เป็นมาตรฐานได้โดยการหารด้วยความยาว เช่น x = ||x|| (เอ็กซ์/||x||) = ||x|| จ- ที่นี่ จ = เอ็กซ์/||x- - เวกเตอร์ที่ทำให้เป็นมาตรฐาน

เวกเตอร์จะถูกเรียกว่าออร์โธนอร์มอลหากพวกมันทั้งหมดถูกทำให้เป็นมาตรฐานและตั้งฉากเป็นคู่

1.10. มุมระหว่างเวกเตอร์

ผลิตภัณฑ์สเกลาร์กำหนดและ มุมφ ระหว่างเวกเตอร์สองตัว xและ ย

ถ้าเวกเตอร์ตั้งฉาก ดังนั้น cosφ = 0 และ φ = π/2 และถ้าเวกเตอร์เหล่านั้นอยู่ในแนวโคลิเนียร์ ดังนั้น cosφ = 1 และ φ = 0

1.11. การแสดงเวกเตอร์ของเมทริกซ์

แต่ละเมทริกซ์ กขนาด ฉัน× เจสามารถแสดงเป็นเซตของเวกเตอร์ได้

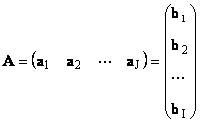
ตรงนี้ทุกเวกเตอร์ ก เจเป็น เจคอลัมน์ที่ 3 และเวกเตอร์แถว ข ฉันเป็น ฉันแถวที่หนึ่งของเมทริกซ์ ก

1.12. เวกเตอร์ที่ขึ้นอยู่กับเชิงเส้น

เวกเตอร์ที่มีมิติเดียวกัน ( เอ็น) สามารถบวกและคูณด้วยตัวเลขได้ เช่นเดียวกับเมทริกซ์ ผลลัพธ์ที่ได้จะเป็นเวกเตอร์ที่มีมิติเดียวกัน ให้มีเวกเตอร์หลายตัวที่มีมิติเดียวกัน x 1 , x 2 ,...,x K และจำนวนตัวเลขเท่ากัน α α 1 , α 2 ,...,α เค- เวกเตอร์

ย= แอลฟา 1 x 1 + แอลฟา 2 x 2 +...+ α เค x เค

เรียกว่า การรวมกันเชิงเส้นเวกเตอร์ x เค .

หากมีตัวเลขที่ไม่ใช่ศูนย์ดังกล่าว α เค ≠ 0, เค = 1,..., เค, อะไร ย = 0 แล้วเซตของเวกเตอร์แบบนั้น x เคเรียกว่า ขึ้นอยู่กับเชิงเส้น- มิฉะนั้นจะเรียกเวกเตอร์ว่าเป็นอิสระเชิงเส้น ตัวอย่างเช่น เวกเตอร์ x 1 = (2, 2)t และ x 2 = (−1, −1) t มีความสัมพันธ์เชิงเส้นตรง เพราะ x 1 +2x 2 = 0

1.13. อันดับเมทริกซ์

พิจารณาชุดของ เคเวกเตอร์ x 1 , x 2 ,...,x เคขนาด เอ็น- อันดับของระบบเวกเตอร์นี้คือจำนวนเวกเตอร์อิสระเชิงเส้นสูงสุด เช่นในชุด

ตัวอย่างเช่น มีเวกเตอร์อิสระเชิงเส้นเพียงสองตัวเท่านั้น x 1 และ x 2 ดังนั้นอันดับของมันคือ 2

แน่นอน หากมีเวกเตอร์ในชุดมากกว่ามิติ ( เค>เอ็น) ดังนั้นพวกมันจึงจำเป็นต้องขึ้นอยู่กับเชิงเส้นตรง

อันดับเมทริกซ์(แสดงด้วยอันดับ ( ก)) คืออันดับของระบบเวกเตอร์ที่ประกอบด้วย แม้ว่าเมทริกซ์ใดๆ จะสามารถแสดงได้สองวิธี (เวกเตอร์คอลัมน์หรือแถว) แต่สิ่งนี้จะไม่ส่งผลต่อค่าอันดับ เนื่องจาก

1.14. เมทริกซ์ผกผัน

เมทริกซ์จตุรัส กเรียกว่าไม่เสื่อมถ้ามีลักษณะเฉพาะ ย้อนกลับเมทริกซ์ ก-1 กำหนดโดยเงื่อนไข

เอเอ −1 = ก −1 ก = ฉัน.

เมทริกซ์ผกผันไม่มีอยู่ในเมทริกซ์ทั้งหมด เงื่อนไขที่จำเป็นและเพียงพอสำหรับการไม่เสื่อมคือ

เดต( ก) ≠ 0 หรืออันดับ ( ก) = เอ็น.

การผกผันเมทริกซ์เป็นขั้นตอนที่ซับซ้อนซึ่งมีโปรแกรมพิเศษ ตัวอย่างเช่น,

ข้าว. 17 การผกผันเมทริกซ์

ให้เรานำเสนอสูตรสำหรับกรณีที่ง่ายที่สุด - เมทริกซ์ 2×2

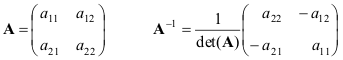
ถ้าเมทริกซ์ กและ บีก็ไม่เสื่อมเสียแล้ว

(เอบี) −1 = บี −1 ก −1 .

1.15. เมทริกซ์ผกผันเทียม

ถ้าเป็นเมทริกซ์ กเป็นเอกพจน์และไม่มีเมทริกซ์ผกผัน ดังนั้นในบางกรณีคุณสามารถใช้ได้ หลอกผกผันเมทริกซ์ซึ่งถูกกำหนดให้เป็นเมทริกซ์ดังกล่าว ก+ นั่น

เอเอ + ก = ก.

เมทริกซ์ pseudoinverse ไม่ใช่เพียงเมทริกซ์เดียวและรูปแบบของมันขึ้นอยู่กับวิธีการก่อสร้าง ตัวอย่างเช่น สำหรับเมทริกซ์สี่เหลี่ยม คุณสามารถใช้วิธี Moore-Penrose

ถ้าจำนวนคอลัมน์น้อยกว่าจำนวนแถวแล้ว

ก + =(กที ก) −1 กที

ตัวอย่างเช่น,

ข้าว. 17a การผกผันหลอกของเมทริกซ์

หากจำนวนคอลัมน์มากกว่าจำนวนแถวแสดงว่า

ก + =กเสื้อ( เอเอเสื้อ) −1

1.16. การคูณเวกเตอร์ด้วยเมทริกซ์

เวกเตอร์ xสามารถคูณด้วยเมทริกซ์ได้ กขนาดที่เหมาะสม ในกรณีนี้ เวกเตอร์คอลัมน์จะถูกคูณทางด้านขวา ขวานและแถวเวกเตอร์อยู่ทางด้านซ้าย xที ก- ถ้าเป็นมิติเวกเตอร์ เจและมิติเมทริกซ์ ฉัน× เจผลลัพธ์ที่ได้จะเป็นเวกเตอร์ของมิติ ฉัน- ตัวอย่างเช่น,

ข้าว. 18 การคูณเวกเตอร์ด้วยเมทริกซ์

ถ้าเป็นเมทริกซ์ ก- สี่เหลี่ยม ( ฉัน× ฉัน) จากนั้นเวกเตอร์ ย = ขวานมีมิติเดียวกันกับ x- เห็นได้ชัดว่า

ก(α1 x 1 + แอลฟา 2 x 2) = α 1 ขวาน 1 + แอลฟา 2 ขวาน 2 .

ดังนั้นเมทริกซ์จึงถือได้ว่าเป็นการแปลงเชิงเส้นของเวกเตอร์ โดยเฉพาะ ทรงเครื่อง = x, วัว = 0 .

2. ข้อมูลเพิ่มเติม

2.1. ระบบสมการเชิงเส้น

อนุญาต ก- ขนาดเมทริกซ์ ฉัน× เจ, ก ข- เวกเตอร์มิติ เจ- พิจารณาสมการ

ขวาน = ข

สัมพันธ์กับเวกเตอร์ x, ขนาด ฉัน- โดยพื้นฐานแล้วมันเป็นระบบของ ฉัน สมการเชิงเส้นกับ เจไม่ทราบ x 1 ,...,x เจ- วิธีแก้ปัญหามีอยู่ก็ต่อเมื่อเท่านั้น

อันดับ ( ก) = อันดับ( บี) = ร,

ที่ไหน บีเป็นเมทริกซ์ขยายของมิติ ฉัน×( เจ+1) ประกอบด้วยเมทริกซ์ กเสริมด้วยคอลัมน์ ข, บี = (ก ข- มิฉะนั้นสมการจะไม่สอดคล้องกัน

ถ้า ร = ฉัน = เจดังนั้นโซลูชันจะไม่ซ้ำกัน

x = ก −1 ข.

ถ้า ร < ฉันจึงมีคำตอบที่แตกต่างกันมากมายที่สามารถแสดงผ่านผลรวมเชิงเส้นได้ เจ−รเวกเตอร์ ระบบ สมการเอกพันธ์ ขวาน = 0 ด้วยเมทริกซ์จตุรัส ก (เอ็น× เอ็น) มี วิธีแก้ปัญหาที่ไม่สำคัญ (x ≠ 0 ) ถ้าและเฉพาะในกรณีที่ det( ก) = 0 ถ้า ร= อันดับ( ก)<เอ็นแล้วก็มี เอ็น−รโซลูชั่นอิสระเชิงเส้น

2.2. รูปแบบไบลิเนียร์และกำลังสอง

ถ้า กเป็นเมทริกซ์จตุรัส และ xและ ย- เวกเตอร์ของมิติที่สอดคล้องกัน จากนั้นเป็นผลคูณสเกลาร์ของแบบฟอร์ม xที อ๋อเรียกว่า ไบลิเนียร์รูปแบบที่กำหนดโดยเมทริกซ์ ก- ที่ x = ยการแสดงออก xที ขวานเรียกว่า กำลังสองรูปร่าง.

2.3. เมทริกซ์แน่นอนเชิงบวก

เมทริกซ์จตุรัส กเรียกว่า บวกแน่นอน, ถ้าสำหรับเวกเตอร์ที่ไม่ใช่ศูนย์ใดๆ x ≠ 0 ,

xที ขวาน > 0.

กำหนดไว้เช่นเดียวกัน เชิงลบ (xที ขวาน < 0), ไม่เป็นลบ (xที ขวาน≥ 0) และ เชิงลบ (xที ขวาน≤ 0) เมทริกซ์บางตัว

2.4. การสลายตัวของโชเลสกี้

ถ้าเมทริกซ์สมมาตร กเป็นบวกแน่นอน แล้วจะมีเมทริกซ์สามเหลี่ยมเฉพาะ คุณด้วยองค์ประกอบเชิงบวกซึ่ง

ก = คุณที คุณ.

ตัวอย่างเช่น,

ข้าว. 19 การสลายตัวของโชเลสกี้

2.5. การสลายตัวของขั้วโลก

อนุญาต กเป็นเมทริกซ์จตุรัสที่ไม่เป็นเอกพจน์ของมิติ เอ็น× เอ็น- แล้วมีความเป็นเอกลักษณ์ ขั้วโลกผลงาน

ก = เอส.อาร์.

ที่ไหน สเป็นเมทริกซ์สมมาตรที่ไม่เป็นลบ และ รเป็นเมทริกซ์มุมฉาก เมทริกซ์ สและ รสามารถกำหนดได้อย่างชัดเจน:

ส 2 = เอเอทีหรือ ส = (เอเอเสื้อ) ½ และ ร = ส −1 ก = (เอเอเสื้อ) −½ ก.

ตัวอย่างเช่น,

ข้าว. 20 การสลายตัวของขั้ว

ถ้าเป็นเมทริกซ์ กเสื่อมลงแล้วการสลายตัวไม่ซ้ำกัน กล่าวคือ สยังคงอยู่คนเดียว แต่ รอาจจะมาก การสลายตัวแบบขั้วแสดงถึงเมทริกซ์ กเป็นการผสมผสานระหว่างการบีบอัด/การขยาย สและเลี้ยว ร.

2.6. เวกเตอร์ลักษณะเฉพาะและค่าลักษณะเฉพาะ

อนุญาต กเป็นเมทริกซ์จตุรัส เวกเตอร์ โวลต์เรียกว่า eigenvectorเมทริกซ์ ก, ถ้า

อ = λ โวลต์,

โดยที่หมายเลข lah ถูกเรียก ค่าลักษณะเฉพาะเมทริกซ์ ก- ดังนั้นการเปลี่ยนแปลงที่เมทริกซ์ดำเนินการ กเหนือเวกเตอร์ โวลต์ลงมาเป็นการยืดหรือบีบอัดอย่างง่ายด้วยค่าสัมประสิทธิ์ แล eigenvector ถูกกำหนดขึ้นอยู่กับการคูณด้วยค่าคงที่ α ≠ 0 เช่น ถ้า โวลต์เป็นเวกเตอร์ลักษณะเฉพาะ แล้ว α โวลต์- ยังเป็นเวกเตอร์ลักษณะเฉพาะอีกด้วย

2.7. ค่าลักษณะเฉพาะ

ที่เมทริกซ์ ก, มิติ ( เอ็น× เอ็น) ต้องไม่เกิน เอ็นค่าลักษณะเฉพาะ พวกเขาตอบสนอง สมการลักษณะเฉพาะ

เดต( ก − λ ฉัน) = 0,

สิ่งมีชีวิต สมการพีชคณิต เอ็น-ลำดับที่ โดยเฉพาะอย่างยิ่งสำหรับเมทริกซ์ 2x2 สมการลักษณะเฉพาะดูเหมือนว่า

ตัวอย่างเช่น,

ข้าว. 21 ค่าลักษณะเฉพาะ

เซตของค่าลักษณะเฉพาะ แลม 1 ,..., แลมบ์ เอ็นเมทริกซ์ กเรียกว่า สเปกตรัม ก.

สเปกตรัมมีคุณสมบัติหลากหลาย โดยเฉพาะ

เดต( ก) = แลมบ์ดา 1 ×...×แลมบ์ เอ็น,สป( ก) = แลมบ์ดา 1 +...+แลม เอ็น.

ค่าลักษณะเฉพาะของเมทริกซ์ที่กำหนดเองสามารถเป็นตัวเลขเชิงซ้อนได้ แต่ถ้าเมทริกซ์มีความสมมาตร ( กเสื้อ = ก) จากนั้นค่าลักษณะเฉพาะของมันก็เป็นจริง

2.8. ไอเกนเวกเตอร์

ที่เมทริกซ์ ก, มิติ ( เอ็น× เอ็น) ต้องไม่เกิน เอ็น eigenvector ซึ่งแต่ละค่าสอดคล้องกับค่าลักษณะเฉพาะของตัวเอง เพื่อกำหนดไอเกนเวคเตอร์ โวลต์ nจำเป็นต้องแก้ระบบสมการเอกพันธ์

(ก − λ n ฉัน)โวลต์ n = 0 .

มันมีวิธีแก้ปัญหาที่ไม่สำคัญ เนื่องจาก det( เอ -λ n ฉัน) = 0.

ตัวอย่างเช่น,

ข้าว. 22 ไอเกนเวกเตอร์

เวกเตอร์ลักษณะเฉพาะของเมทริกซ์สมมาตรนั้นตั้งฉาก

ค่าลักษณะเฉพาะ (ตัวเลข) และ เวกเตอร์ลักษณะเฉพาะ.
ตัวอย่างการแก้ปัญหา

เป็นตัวของตัวเอง

จากสมการทั้งสองจึงเป็นไปตามนั้น

เอาเป็นว่า: .

เป็นผลให้: – เวกเตอร์ลักษณะเฉพาะตัวที่สอง

ให้เราทำซ้ำประเด็นสำคัญของการตัดสินใจ:

– ระบบผลลัพธ์ย่อมมีวิธีแก้ปัญหาทั่วไป (สมการขึ้นอยู่กับเชิงเส้นตรง)

– เราเลือก "y" ในลักษณะที่เป็นจำนวนเต็มและพิกัด "x" แรกเป็นจำนวนเต็ม บวก และเล็กที่สุดเท่าที่จะเป็นไปได้

– เราตรวจสอบว่าคำตอบเฉพาะนั้นเป็นไปตามแต่ละสมการของระบบ

คำตอบ .

มี "จุดตรวจ" ระดับกลางค่อนข้างเพียงพอ ดังนั้น โดยหลักการแล้ว การตรวจสอบความเท่าเทียมกันจึงไม่จำเป็น

ในแหล่งข้อมูลต่างๆ พิกัดของเวกเตอร์ลักษณะเฉพาะมักไม่ได้เขียนเป็นคอลัมน์ แต่เขียนเป็นแถว เช่น (และบอกตามตรงว่าฉันเองก็เคยชินกับการจดมันลงในบรรทัด)- ตัวเลือกนี้เป็นที่ยอมรับ แต่ในแง่ของหัวข้อ การแปลงเชิงเส้นในทางเทคนิคแล้วสะดวกกว่าในการใช้งาน เวกเตอร์คอลัมน์.

บางทีวิธีแก้ปัญหาอาจดูยาวมากสำหรับคุณ แต่นี่เป็นเพียงเพราะฉันแสดงความคิดเห็นอย่างละเอียดในตัวอย่างแรกเท่านั้น

ตัวอย่างที่ 2

เมทริกซ์

มาฝึกด้วยตัวเองกันเถอะ! ตัวอย่างงานสุดท้ายโดยประมาณในตอนท้ายของบทเรียน

บางครั้งคุณจำเป็นต้องทำ งานเพิ่มเติมกล่าวคือ:

เขียนการสลายตัวของเมทริกซ์แบบบัญญัติ

มันคืออะไร?

ถ้าเวกเตอร์ลักษณะเฉพาะของเมทริกซ์ก่อตัว พื้นฐานจากนั้นจึงสามารถแสดงเป็น:

เมทริกซ์ประกอบด้วยพิกัดของเวกเตอร์ลักษณะเฉพาะอยู่ที่ไหน – เส้นทแยงมุมเมทริกซ์ที่มีค่าลักษณะเฉพาะที่สอดคล้องกัน

การสลายตัวของเมทริกซ์นี้เรียกว่า ตามบัญญัติหรือ เส้นทแยงมุม.

ลองดูที่เมทริกซ์ของตัวอย่างแรก เวกเตอร์ลักษณะเฉพาะของมัน เป็นอิสระเชิงเส้น(ไม่ใช่คอลลิเนียร์) และสร้างเป็นพื้นฐาน มาสร้างเมทริกซ์พิกัดกัน:

บน เส้นทแยงมุมหลักเมทริกซ์ ในลำดับที่เหมาะสมมีค่าลักษณะเฉพาะอยู่และองค์ประกอบที่เหลือมีค่าเท่ากับศูนย์:
– ฉันเน้นย้ำถึงความสำคัญของลำดับอีกครั้ง: “สอง” สอดคล้องกับเวกเตอร์ที่ 1 และดังนั้นจึงอยู่ในคอลัมน์ที่ 1 “สาม” – ถึงเวกเตอร์ที่ 2

ใช้อัลกอริธึมปกติในการค้นหา เมทริกซ์ผกผันหรือ วิธีเกาส์-จอร์แดนเราพบ - ไม่ นั่นไม่ได้พิมพ์ผิด! - ตรงหน้าคุณเป็นเหตุการณ์ที่เกิดขึ้นไม่บ่อยนัก เช่น สุริยุปราคา ซึ่งการกลับด้านเกิดขึ้นใกล้กับเมทริกซ์ดั้งเดิม

ยังคงต้องเขียนการสลายตัวของเมทริกซ์ตามรูปแบบบัญญัติ:

ระบบสามารถแก้ไขได้โดยใช้ การเปลี่ยนแปลงเบื้องต้นและในตัวอย่างต่อไปนี้ เราจะใช้วิธีนี้ แต่ที่นี่วิธีการ "โรงเรียน" ทำงานได้เร็วกว่ามาก จากสมการที่ 3 เราแสดง: – แทนที่ในสมการที่สอง:

เนื่องจากพิกัดแรกเป็นศูนย์ เราจึงได้ระบบ จากแต่ละสมการที่เป็นไปตามนั้น

และอีกครั้ง ให้ความสนใจกับการมีอยู่ของความสัมพันธ์เชิงเส้น- หากได้รับวิธีแก้ปัญหาเพียงเล็กน้อยเท่านั้น จากนั้นพบค่าลักษณะเฉพาะอย่างไม่ถูกต้อง หรือระบบถูกคอมไพล์/แก้ไขโดยมีข้อผิดพลาด

พิกัดแบบกระชับจะให้ค่า

ไอเกนเวกเตอร์:

และอีกครั้งเราตรวจสอบวิธีแก้ปัญหาที่พบ ตอบสนองทุกสมการของระบบ- ในย่อหน้าถัดไปและในงานต่อ ๆ ไป ฉันขอแนะนำให้ใช้ความปรารถนานี้เป็นกฎบังคับ

2) สำหรับค่าลักษณะเฉพาะ เราจะได้ระบบต่อไปนี้โดยใช้หลักการเดียวกัน:

จากสมการที่ 2 ของระบบ เราแสดง: – แทนที่ในสมการที่สาม:

เนื่องจากพิกัด "ซีตา" เท่ากับศูนย์ เราจึงได้ระบบจากแต่ละสมการที่ตามมา การพึ่งพาเชิงเส้น.

อนุญาต

การตรวจสอบวิธีแก้ปัญหา ตอบสนองทุกสมการของระบบ

ดังนั้น eigenvector คือ:

3) และสุดท้าย ระบบก็สอดคล้องกับค่าลักษณะเฉพาะ:

สมการที่สองดูง่ายที่สุด ดังนั้นมาแสดงสมการนี้และแทนที่มันลงในสมการที่ 1 และ 3 กัน:

ทุกอย่างเรียบร้อยดี - มีความสัมพันธ์เชิงเส้นเกิดขึ้นซึ่งเราแทนที่เป็นนิพจน์:

เป็นผลให้ "x" และ "y" ถูกแสดงผ่าน "z": ในทางปฏิบัติ ไม่จำเป็นต้องบรรลุความสัมพันธ์ดังกล่าวอย่างแม่นยำ ในบางกรณี จะสะดวกกว่าที่จะแสดงทั้งผ่าน หรือ และผ่าน หรือแม้แต่ "ฝึก" - เช่น "X" ถึง "I" และ "I" ถึง "Z"

เอาเป็นว่า:

เราตรวจสอบว่าพบวิธีแก้ปัญหาแล้ว เป็นไปตามแต่ละสมการของระบบและเขียนเวกเตอร์ลักษณะเฉพาะตัวที่สาม

คำตอบ: เวกเตอร์ลักษณะเฉพาะ:

ในเชิงเรขาคณิต เวกเตอร์เหล่านี้กำหนดทิศทางเชิงพื้นที่ที่แตกต่างกันสามทิศทาง ("ไปมา")ตามนั้น การแปลงเชิงเส้นแปลงเวกเตอร์ที่ไม่ใช่ศูนย์ (eigenvectors) เป็นเวกเตอร์คอลลิเนียร์

หากเงื่อนไขจำเป็นต้องค้นหาการสลายตัวตามแบบบัญญัติ สิ่งนี้เป็นไปได้ที่นี่เพราะ ค่าลักษณะเฉพาะที่แตกต่างกันสอดคล้องกับค่าลักษณะเฉพาะอิสระเชิงเส้นที่แตกต่างกัน การสร้างเมทริกซ์ จากพิกัดของมันคือเมทริกซ์แนวทแยง จาก ที่เกี่ยวข้องค่าลักษณะเฉพาะและค้นหา เมทริกซ์ผกผัน .

หากตามเงื่อนไขคุณต้องเขียน เมทริกซ์การแปลงเชิงเส้นโดยใช้เวกเตอร์ลักษณะเฉพาะแล้วเราจะให้คำตอบในรูปแบบ มีความแตกต่างและความแตกต่างก็สำคัญ!เพราะเมทริกซ์นี้คือเมทริกซ์ “de”

ปัญหาเกี่ยวกับการคำนวณที่ง่ายกว่าให้คุณแก้ไขได้ด้วยตัวเอง:

ตัวอย่างที่ 5

ค้นหาเวกเตอร์ลักษณะเฉพาะของการแปลงเชิงเส้นที่กำหนดโดยเมทริกซ์

เมื่อค้นหาตัวเลขของคุณเอง พยายามอย่าไปจนสุดถึงพหุนามดีกรีที่ 3 นอกจากนี้ โซลูชันระบบของคุณอาจแตกต่างจากโซลูชันของฉัน - ไม่มีความแน่นอนในที่นี้ และเวกเตอร์ที่คุณพบอาจแตกต่างจากเวกเตอร์ตัวอย่างขึ้นอยู่กับสัดส่วนของพิกัดที่เกี่ยวข้อง ตัวอย่างเช่น และ. การนำเสนอคำตอบในรูปแบบจะสวยงามกว่า แต่ก็ไม่เป็นไรหากคุณหยุดที่ตัวเลือกที่สอง อย่างไรก็ตาม มีข้อจำกัดที่สมเหตุสมผลสำหรับทุกสิ่ง เวอร์ชันนี้ดูไม่ดีนักอีกต่อไป

ตัวอย่างงานสุดท้ายโดยประมาณในตอนท้ายของบทเรียน

จะแก้ไขปัญหาในกรณีที่มีค่าลักษณะเฉพาะหลายค่าได้อย่างไร

อัลกอริธึมทั่วไปยังคงเหมือนเดิม แต่มีลักษณะเฉพาะของตัวเอง และขอแนะนำให้เก็บวิธีแก้ปัญหาบางส่วนไว้ในรูปแบบวิชาการที่เข้มงวดกว่านี้:

ตัวอย่างที่ 6

ค้นหาค่าลักษณะเฉพาะและเวกเตอร์ลักษณะเฉพาะ

สารละลาย

แน่นอนว่า เราจะมาใช้ประโยชน์จากคอลัมน์แรกสุดอลังการกันดีกว่า:

และหลังจากแยกตัวประกอบตรีโกณมิติกำลังสองแล้ว:

เป็นผลให้ได้รับค่าลักษณะเฉพาะซึ่งสองค่านั้นเป็นทวีคูณ

มาหาเวกเตอร์ลักษณะเฉพาะกัน:

1) มาจัดการกับทหารคนเดียวตามโครงการ "เรียบง่าย":

จากสมการสองสมการสุดท้ายจะมองเห็นความเท่าเทียมกันได้ชัดเจนซึ่งแน่นอนว่าควรแทนที่ลงในสมการที่ 1 ของระบบ:

คุณจะไม่พบชุดค่าผสมที่ดีกว่า:
ไอเกนเวกเตอร์:

2-3) ตอนนี้เราลบยามสองสามคนออก ในกรณีนี้อาจกลายเป็นว่า สองหรือหนึ่งอย่างใดอย่างหนึ่ง eigenvector ไม่ว่ารากจะมีหลายหลาก เราก็แทนค่าลงในดีเทอร์มิแนนต์ ซึ่งนำเราไปสู่สิ่งต่อไป ระบบเอกพันธ์ของสมการเชิงเส้น:

Eigenvector ก็คือเวกเตอร์นั่นเอง
ระบบพื้นฐานของการแก้ปัญหา

จริงๆ แล้ว ตลอดทั้งบทเรียน เราไม่ได้ทำอะไรเลยนอกจากค้นหาเวกเตอร์ของระบบพื้นฐาน เพียงแต่ว่าคำนี้ไม่จำเป็นอย่างยิ่งในขณะนี้ อย่างไรก็ตาม นักเรียนที่ฉลาดเหล่านั้นที่พลาดหัวข้อในชุดลายพราง สมการเอกพันธ์จะถูกบังคับให้สูบบุหรี่แล้ว

การดำเนินการเพียงอย่างเดียวคือการลบบรรทัดพิเศษออก ผลลัพธ์ที่ได้คือเมทริกซ์ขนาด 1 x 3 โดยมี "ขั้นตอน" อย่างเป็นทางการอยู่ตรงกลาง
– ตัวแปรพื้นฐาน – ตัวแปรอิสระ มีตัวแปรอิสระสองตัว ดังนั้น นอกจากนี้ยังมีเวกเตอร์สองตัวของระบบพื้นฐานอีกด้วย.

เรามาแสดงตัวแปรพื้นฐานในรูปของตัวแปรอิสระกัน: ปัจจัยศูนย์ที่อยู่หน้า "X" ช่วยให้สามารถรับค่าใด ๆ ก็ได้ (ซึ่งมองเห็นได้ชัดเจนจากระบบสมการ)

ในบริบทของปัญหานี้ จะสะดวกกว่าถ้าเขียนวิธีแก้ปัญหาทั่วไปไม่เรียงกัน แต่เขียนเป็นคอลัมน์:

ทั้งคู่สอดคล้องกับ eigenvector:
ทั้งคู่สอดคล้องกับ eigenvector:

บันทึก : ผู้อ่านที่เชี่ยวชาญสามารถเลือกเวกเตอร์เหล่านี้ได้ด้วยวาจา - เพียงแค่วิเคราะห์ระบบ แต่จำเป็นต้องมีความรู้บางอย่างที่นี่ มีตัวแปรสามตัว อันดับเมทริกซ์ของระบบ- หนึ่งซึ่งหมายถึง ระบบการตัดสินใจขั้นพื้นฐานประกอบด้วยเวกเตอร์ 3 – 1 = 2 ตัว อย่างไรก็ตาม เวกเตอร์ที่พบจะมองเห็นได้ชัดเจนแม้จะไม่มีความรู้นี้ก็ตาม โดยเป็นเพียงระดับสัญชาตญาณเท่านั้น ในกรณีนี้ เวกเตอร์ที่สามจะถูกเขียนให้ "สวยงาม" ยิ่งขึ้น: อย่างไรก็ตาม ฉันขอเตือนคุณว่าในอีกตัวอย่างหนึ่ง การเลือกแบบง่ายๆ อาจไม่สามารถทำได้ ซึ่งเป็นเหตุผลว่าทำไมประโยคนี้จึงมีไว้สำหรับผู้ที่มีประสบการณ์ นอกจากนี้ ทำไมไม่ลองพูดเป็นเวกเตอร์ที่สามดูล่ะ? ท้ายที่สุดแล้ว พิกัดของมันก็เป็นไปตามแต่ละสมการของระบบและเวกเตอร์ด้วย เป็นอิสระเชิงเส้น โดยหลักการแล้วตัวเลือกนี้เหมาะสม แต่ "คด" เนื่องจากเวกเตอร์ "อื่น ๆ " เป็นการรวมกันเชิงเส้นของเวกเตอร์ของระบบพื้นฐาน

คำตอบ: ค่าลักษณะเฉพาะ: , เวกเตอร์ลักษณะเฉพาะ:

ตัวอย่างที่คล้ายกันสำหรับโซลูชันอิสระ:

ตัวอย่างที่ 7

ค้นหาค่าลักษณะเฉพาะและเวกเตอร์ลักษณะเฉพาะ

ตัวอย่างการออกแบบขั้นสุดท้ายโดยประมาณในตอนท้ายของบทเรียน

ควรสังเกตว่าในตัวอย่างที่ 6 และ 7 จะได้รับ eigenvectors อิสระเชิงเส้นสามเท่าดังนั้นเมทริกซ์ดั้งเดิมจึงสามารถแสดงได้ในการสลายตัวตามรูปแบบบัญญัติ แต่ราสเบอร์รี่ดังกล่าวไม่ได้เกิดขึ้นในทุกกรณี:

ตัวอย่างที่ 8

สารละลาย: มาสร้างและแก้สมการคุณลักษณะกันดีกว่า:

มาขยายดีเทอร์มิแนนต์ในคอลัมน์แรก:

เราดำเนินการลดความซับซ้อนเพิ่มเติมตามวิธีการที่พิจารณา โดยหลีกเลี่ยงพหุนามดีกรีที่ 3:

– ค่าลักษณะเฉพาะ

มาหาเวกเตอร์ลักษณะเฉพาะกัน:

1) ไม่มีปัญหากับรูท:

อย่าแปลกใจเลย นอกจากชุดอุปกรณ์แล้ว ยังมีตัวแปรที่ใช้งานอยู่ด้วย ซึ่งก็ไม่มีความแตกต่างกัน

จากสมการที่ 3 เราแสดงมันและแทนที่มันลงในสมการที่ 1 และ 2:

จากสมการทั้งสองดังนี้:

ให้แล้ว:

2-3) สำหรับหลายค่าเราได้รับระบบ .

ลองเขียนเมทริกซ์ของระบบแล้วใช้การแปลงเบื้องต้น ทำให้มันอยู่ในรูปแบบขั้นตอน:

เวกเตอร์ลักษณะเฉพาะของเมทริกซ์จตุรัสคือค่าหนึ่งที่เมื่อคูณด้วยเมทริกซ์ที่กำหนด จะทำให้เกิดเวกเตอร์คอลลิเนียร์ ด้วยคำพูดง่ายๆเมื่อคูณเมทริกซ์ด้วยเวกเตอร์ลักษณะเฉพาะ ค่าหลังจะยังคงเหมือนเดิม แต่คูณด้วยจำนวนที่แน่นอน

คำนิยาม

เวกเตอร์ลักษณะเฉพาะคือเวกเตอร์ V ที่ไม่เป็นศูนย์ ซึ่งเมื่อคูณด้วยเมทริกซ์จตุรัส M แล้วตัวมันเองจะเพิ่มขึ้นด้วยตัวเลขจำนวนหนึ่ง แล ในสัญกรณ์พีชคณิตดูเหมือนว่า:

ม × วี = แลมบ์ × วี

โดยที่ แล คือค่าลักษณะเฉพาะของเมทริกซ์ M

ลองดูตัวอย่างเชิงตัวเลข เพื่อความสะดวกในการบันทึก ตัวเลขในเมทริกซ์จะถูกคั่นด้วยเครื่องหมายอัฒภาค ขอให้เรามีเมทริกซ์:

• ม = 0; 4;
• 6; 10.

ลองคูณด้วยเวกเตอร์คอลัมน์:

• วี = -2;

เมื่อเราคูณเมทริกซ์ด้วยเวกเตอร์คอลัมน์ เราจะได้เวกเตอร์คอลัมน์ด้วย ในภาษาคณิตศาสตร์ที่เข้มงวด สูตรสำหรับการคูณเมทริกซ์ 2 × 2 ด้วยเวกเตอร์คอลัมน์จะมีลักษณะดังนี้:

• ม × วี = M11 × V11 + M12 × V21;
• M21 × V11 + M22 × V21

M11 หมายถึงองค์ประกอบของเมทริกซ์ M ที่อยู่ในแถวแรกและคอลัมน์แรก และ M22 หมายถึงองค์ประกอบที่อยู่ในแถวที่สองและคอลัมน์ที่สอง สำหรับเมทริกซ์ของเรา องค์ประกอบเหล่านี้จะเท่ากับ M11 = 0, M12 = 4, M21 = 6, M22 10 สำหรับเวกเตอร์คอลัมน์ ค่าเหล่านี้จะเท่ากับ V11 = –2, V21 = 1 ตามสูตรนี้ เราได้รับผลลัพธ์ของผลิตภัณฑ์ของเมทริกซ์จตุรัสด้วยเวกเตอร์ดังต่อไปนี้:

• ม × วี = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2

เพื่อความสะดวก ลองเขียนเวกเตอร์คอลัมน์ลงในแถวกัน ดังนั้นเราจึงคูณเมทริกซ์จตุรัสด้วยเวกเตอร์ (-2; 1) ผลลัพธ์ที่ได้คือเวกเตอร์ (4; -2) แน่นอนว่านี่คือเวกเตอร์เดียวกันคูณด้วย แล = -2 แลมบ์ดาในกรณีนี้แสดงถึงค่าลักษณะเฉพาะของเมทริกซ์

eigenvector ของเมทริกซ์คือเวกเตอร์ collinear นั่นคือวัตถุที่ไม่เปลี่ยนตำแหน่งในอวกาศเมื่อคูณด้วยเมทริกซ์ แนวคิดเรื่องความเป็นเส้นตรงในพีชคณิตเวกเตอร์มีความคล้ายคลึงกับคำว่าความเท่าเทียมในเรขาคณิต ในการตีความทางเรขาคณิต เวกเตอร์คอลลิเนียร์เป็นส่วนที่มีทิศทางขนานกันซึ่งมีความยาวต่างกัน ตั้งแต่สมัยยุคลิด เรารู้ว่าเส้นตรงหนึ่งเส้นมีจำนวนเส้นขนานกับเส้นตรงเป็นอนันต์ ดังนั้นจึงมีเหตุผลที่จะสรุปได้ว่าแต่ละเมทริกซ์มีจำนวนเวกเตอร์ลักษณะเฉพาะที่ไม่มีที่สิ้นสุด

จากตัวอย่างก่อนหน้านี้ เห็นได้ชัดว่า eigenvector สามารถเป็น (-8; 4) และ (16; -8) และ (32, -16) เหล่านี้คือเวกเตอร์คอลลิเนียร์ทั้งหมดที่สอดคล้องกับค่าลักษณะเฉพาะ แล = -2 เมื่อคูณเมทริกซ์ดั้งเดิมด้วยเวกเตอร์เหล่านี้ เราจะยังได้เวกเตอร์ที่แตกต่างจากต้นฉบับ 2 เท่า นั่นคือเหตุผลที่เมื่อแก้ไขปัญหาในการค้นหาเวกเตอร์ลักษณะเฉพาะ จำเป็นต้องค้นหาเฉพาะวัตถุเวกเตอร์ที่เป็นอิสระเชิงเส้นเท่านั้น ส่วนใหญ่แล้ว สำหรับเมทริกซ์ขนาด n × n จะมีเวกเตอร์ลักษณะเฉพาะจำนวน n จำนวน เครื่องคิดเลขของเราออกแบบมาเพื่อการวิเคราะห์เมทริกซ์กำลังสองอันดับสอง ดังนั้นผลลัพธ์จะพบเวกเตอร์ลักษณะเฉพาะสองตัวเกือบทุกครั้ง ยกเว้นกรณีที่ตรงกัน

ในตัวอย่างข้างต้น เรารู้เวกเตอร์ลักษณะเฉพาะของเมทริกซ์ดั้งเดิมล่วงหน้า และระบุจำนวนแลมบ์ดาอย่างชัดเจน อย่างไรก็ตามในทางปฏิบัติทุกอย่างเกิดขึ้นในทางตรงกันข้าม: ค่าลักษณะเฉพาะจะถูกค้นพบก่อนและหลังค่าลักษณะเฉพาะเท่านั้น

อัลกอริธึมโซลูชัน

ลองดูเมทริกซ์ M เดิมอีกครั้งแล้วลองหาเวกเตอร์ลักษณะเฉพาะของมันทั้งสองตัว ดังนั้นเมทริกซ์จึงมีลักษณะดังนี้:

• ม = 0; 4;
• 6; 10.

ก่อนอื่น เราต้องกำหนดค่าลักษณะเฉพาะ แล ซึ่งต้องคำนวณดีเทอร์มิแนนต์ของเมทริกซ์ต่อไปนี้:

• (0 - แลม); 4;
• 6; (10 - แลม)

เมทริกซ์นี้ได้มาจากการลบค่าที่ไม่รู้จัก γ ออกจากองค์ประกอบบนเส้นทแยงมุมหลัก ดีเทอร์มิแนนต์ถูกกำหนดโดยใช้สูตรมาตรฐาน:

• detA = M11 × M21 − M12 × M22
• detA = (0 − แลม) × (10 − แลม) − 24

เนื่องจากเวกเตอร์ของเราต้องไม่เป็นศูนย์ เราจึงยอมรับสมการผลลัพธ์ที่ขึ้นอยู่กับเชิงเส้นตรง และถือว่าดีเทอร์มีแนนต์ detA ของเราเป็นศูนย์

(0 - แลมบ์ดา) × (10 - แลมบ์ดา) - 24 = 0

ลองเปิดวงเล็บแล้วรับสมการคุณลักษณะของเมทริกซ์:

แล 2 - 10 แล - 24 = 0

นี่คือมาตรฐาน สมการกำลังสองซึ่งจะต้องแก้ไขด้วยการแยกแยะ

D = ข 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196

รากของการจำแนกคือ sqrt(D) = 14 ดังนั้น แลมบ์ดา = -2, แลมบ์ดา = 12 ทีนี้สำหรับค่าแลมบ์ดาแต่ละค่า เราจำเป็นต้องหาเวกเตอร์ลักษณะเฉพาะ ให้เราแสดงค่าสัมประสิทธิ์ของระบบสำหรับ แล = -2

• M - แลมบ์ × E = 2; 4;
• 6; 12.

ในสูตรนี้ E คือเมทริกซ์เอกลักษณ์ จากเมทริกซ์ผลลัพธ์ เราสร้างระบบสมการเชิงเส้น:

2x + 4y = 6x + 12y,

โดยที่ x และ y เป็นองค์ประกอบเวกเตอร์ลักษณะเฉพาะ

มารวบรวม X ทั้งหมดทางด้านซ้ายและ Y ทั้งหมดทางด้านขวา แน่นอน - 4x = 8y หารนิพจน์ด้วย - 4 แล้วได้ x = –2y ตอนนี้เราสามารถกำหนด eigenvector แรกของเมทริกซ์ได้โดยรับค่าใด ๆ ของสิ่งที่ไม่รู้จัก (จำค่าอนันต์ของ eigenvector ที่ขึ้นกับเชิงเส้นตรง) ลองหา y = 1 จากนั้น x = –2 ดังนั้น eigenvector ตัวแรกจะมีลักษณะดังนี้ V1 = (–2; 1) กลับไปที่จุดเริ่มต้นของบทความ วัตถุเวกเตอร์นี้เองที่เราคูณเมทริกซ์ด้วยเพื่อแสดงแนวคิดของเวกเตอร์ลักษณะเฉพาะ

ทีนี้ลองหาเวกเตอร์ลักษณะเฉพาะของ แล = 12 กัน

• ม - แลม× E = -12; 4
• 6; -2.

มาสร้างระบบสมการเชิงเส้นแบบเดียวกันกัน

• -12x + 4y = 6x − 2y
• -18x = -6ป
• 3x = ย

ตอนนี้เราหา x = 1 ดังนั้น y = 3 ดังนั้น เวกเตอร์ลักษณะเฉพาะตัวที่สองจะดูเหมือน V2 = (1; 3) เมื่อคูณเมทริกซ์ดั้งเดิมด้วยเวกเตอร์ที่กำหนด ผลลัพธ์จะเป็นเวกเตอร์เดียวกันคูณด้วย 12 เสมอ นี่คือจุดที่อัลกอริทึมของการแก้ปัญหาสิ้นสุดลง ตอนนี้คุณรู้วิธีกำหนดเวกเตอร์ลักษณะเฉพาะของเมทริกซ์ด้วยตนเองแล้ว

• ปัจจัยกำหนด;
• ติดตามนั่นคือผลรวมขององค์ประกอบบนเส้นทแยงมุมหลัก
• อันดับ ซึ่งก็คือจำนวนสูงสุดของแถว/คอลัมน์ที่เป็นอิสระเชิงเส้น

โปรแกรมทำงานตามอัลกอริธึมข้างต้น ช่วยลดขั้นตอนการแก้ปัญหาให้ได้มากที่สุด สิ่งสำคัญคือต้องชี้ให้เห็นว่าในโปรแกรม lambda ถูกกำหนดด้วยตัวอักษร "c" ลองดูตัวอย่างเชิงตัวเลข

ตัวอย่างการทำงานของโปรแกรม

ลองหาเวกเตอร์ลักษณะเฉพาะสำหรับเมทริกซ์ต่อไปนี้:

• ม = 5; 13;
• 4; 14.

ป้อนค่าเหล่านี้ลงในเซลล์ของเครื่องคิดเลขและรับคำตอบในรูปแบบต่อไปนี้:

• อันดับเมทริกซ์: 2;
• ดีเทอร์มิแนนต์เมทริกซ์: 18;
• การติดตามเมทริกซ์: 19;
• การคำนวณไอเกนเวคเตอร์: c 2 − 19.00c + 18.00 (สมการคุณลักษณะ);
• การคำนวณ Eigenvector: 18 (ค่าแลมบ์ดาแรก);
• การคำนวณ Eigenvector: 1 (ค่าแลมบ์ดาที่สอง);
• ระบบสมการของเวกเตอร์ 1: -13x1 + 13y1 = 4x1 − 4y1;
• ระบบสมการของเวกเตอร์ 2: 4x1 + 13y1 = 4x1 + 13y1;
• ไอเกนเวกเตอร์ 1: (1; 1);
• ไอเกนเวกเตอร์ 2: (-3.25; 1)

ดังนั้นเราจึงได้ไอเกนเวคเตอร์อิสระเชิงเส้นสองตัว

บทสรุป

พีชคณิตเชิงเส้นและ เรขาคณิตเชิงวิเคราะห์- วิชามาตรฐานสำหรับนักศึกษาใหม่ในสาขาวิชาเฉพาะทางด้านเทคนิค ปริมาณมากเวกเตอร์และเมทริกซ์นั้นน่ากลัว และในการคำนวณที่ยุ่งยากเช่นนี้ จึงเกิดข้อผิดพลาดได้ง่าย โปรแกรมของเราจะช่วยให้นักเรียนตรวจสอบการคำนวณหรือแก้ปัญหาการค้นหาเวกเตอร์ลักษณะเฉพาะได้โดยอัตโนมัติ มีเครื่องคิดเลขพีชคณิตเชิงเส้นอื่นๆ ในแค็ตตาล็อกของเรา ใช้ในการศึกษาหรือทำงานของคุณ

สำหรับเมทริกซ์ A หากมีตัวเลข l ดังนั้น AX = lX

ในกรณีนี้จะเรียกหมายเลข l ค่าลักษณะเฉพาะตัวดำเนินการ (เมทริกซ์ A) ที่สอดคล้องกับเวกเตอร์ X

กล่าวอีกนัยหนึ่ง eigenvector คือเวกเตอร์ที่ภายใต้การกระทำของตัวดำเนินการเชิงเส้น แปลงสภาพเป็นเวกเตอร์คอลลิเนียร์ กล่าวคือ แค่คูณด้วยจำนวนหนึ่ง ในทางตรงกันข้าม เวกเตอร์ที่ไม่เหมาะสมจะแปลงได้ยากกว่า

ลองเขียนคำจำกัดความของ eigenvector ในรูปแบบของระบบสมการ:

ย้ายเงื่อนไขทั้งหมดไปทางซ้าย:

ระบบหลังสามารถเขียนได้ในรูปแบบเมทริกซ์ดังนี้

(A - lE)X = O

ระบบผลลัพธ์จะมีคำตอบเป็นศูนย์เสมอ X = O ระบบดังกล่าวซึ่งมีเงื่อนไขอิสระทั้งหมดเท่ากับศูนย์จะถูกเรียก เป็นเนื้อเดียวกัน- หากเมทริกซ์ของระบบดังกล่าวเป็นรูปสี่เหลี่ยมจัตุรัสและดีเทอร์มิแนนต์ไม่เท่ากับศูนย์ ดังนั้นเมื่อใช้สูตรของแครมเมอร์ เราจะได้คำตอบเฉพาะเสมอ - ศูนย์ สามารถพิสูจน์ได้ว่าระบบมีวิธีแก้ปัญหาที่ไม่เป็นศูนย์ก็ต่อเมื่อดีเทอร์มีแนนต์ของเมทริกซ์นี้เท่ากับศูนย์เท่านั้น เช่น

|เอ - เลอี| - = 0

สมการนี้ที่ไม่ทราบค่า l เรียกว่า สมการลักษณะเฉพาะ (พหุนามลักษณะเฉพาะ) เมทริกซ์ A (ตัวดำเนินการเชิงเส้น)

สามารถพิสูจน์ได้ว่าพหุนามคุณลักษณะของตัวดำเนินการเชิงเส้นไม่ได้ขึ้นอยู่กับการเลือกพื้นฐาน

ตัวอย่างเช่น ลองหาค่าลักษณะเฉพาะและเวกเตอร์ลักษณะเฉพาะของตัวดำเนินการเชิงเส้นที่กำหนดโดยเมทริกซ์ A =

เมื่อต้องการทำเช่นนี้ เรามาสร้างสมการคุณลักษณะ |A - lE| กัน - = (1 - ลิตร) 2 - 36 = 1 - 2ล. + ลิตร 2 - 36 = ลิตร 2 - 2ล. - 35 = 0; ง = 4 + 140 = 144; ค่าลักษณะเฉพาะ l 1 = (2 - 12)/2 = -5; ลิตร 2 = (2 + 12)/2 = 7

ในการค้นหาเวกเตอร์ลักษณะเฉพาะ เราจะแก้สมการสองระบบ

(A + 5E)X = O

(A - 7E)X = O

ประการแรกเมทริกซ์แบบขยายจะอยู่ในรูปแบบ

,

โดยที่ x 2 = c, x 1 + (2/3)c = 0; x 1 = -(2/3)s เช่น X (1) = (-(2/3)s; s)

ประการที่สองเมทริกซ์ที่ขยายจะอยู่ในรูปแบบ

,

จากที่ไหน x 2 = c 1, x 1 - (2/3)c 1 = 0; x 1 = (2/3)s 1 เช่น X (2) = ((2/3)s 1; s 1)

ดังนั้น เวกเตอร์ลักษณะเฉพาะของตัวดำเนินการเชิงเส้นนี้คือเวกเตอร์ทั้งหมดของรูปแบบ (-(2/3)с; с) ที่มีค่าลักษณะเฉพาะ (-5) และเวกเตอร์ทั้งหมดของรูปแบบ ((2/3)с 1 ; с 1) ด้วย ค่าลักษณะเฉพาะ 7

สามารถพิสูจน์ได้ว่าเมทริกซ์ของตัวดำเนินการ A บนพื้นฐานที่ประกอบด้วยเวกเตอร์ลักษณะเฉพาะนั้นเป็นเส้นทแยงมุมและมีรูปแบบ:

,

โดยที่ ฉัน คือค่าลักษณะเฉพาะของเมทริกซ์นี้

กลับกันก็เป็นจริงเช่นกัน: หากเมทริกซ์ A ในบางฐานเป็นเส้นทแยงมุม เวกเตอร์ทั้งหมดของฐานนี้จะเป็นเวกเตอร์ลักษณะเฉพาะของเมทริกซ์นี้

นอกจากนี้ยังสามารถพิสูจน์ได้ว่าหากตัวดำเนินการเชิงเส้นมีค่าลักษณะเฉพาะที่แตกต่างกันเป็นคู่ ดังนั้นเวกเตอร์ลักษณะเฉพาะที่สอดคล้องกันจะเป็นอิสระเชิงเส้น และเมทริกซ์ของตัวดำเนินการนี้บนพื้นฐานที่สอดคล้องกันจะมีรูปแบบแนวทแยง

เรามาอธิบายสิ่งนี้ด้วยตัวอย่างก่อนหน้านี้ ลองใช้ค่าที่ไม่ใช่ศูนย์โดยพลการ c และ c 1 แต่เพื่อให้เวกเตอร์ X (1) และ X (2) มีความเป็นอิสระเชิงเส้นเช่น จะเป็นการสร้างพื้นฐาน ตัวอย่างเช่น ให้ c = c 1 = 3 จากนั้น X (1) = (-2; 3), X (2) = (2; 3)

มาตรวจสอบให้แน่ใจกัน ความเป็นอิสระเชิงเส้นเวกเตอร์เหล่านี้:

12 ≠ 0 ในพื้นฐานใหม่นี้ เมทริกซ์ A จะอยู่ในรูปแบบ A * =

เพื่อยืนยันสิ่งนี้ ให้ใช้สูตร A * = C -1 AC ก่อนอื่น มาหา C -1 กันก่อน

ค -1 = ;

รูปร่างกำลังสอง

รูปร่างกำลังสอง f(x 1, x 2, x n) ของตัวแปร n ตัวเรียกว่าผลรวม ซึ่งแต่ละเทอมจะเป็นกำลังสองของตัวแปรตัวใดตัวหนึ่ง หรือผลคูณของตัวแปรสองตัวที่ต่างกัน ซึ่งใช้ค่าสัมประสิทธิ์ที่แน่นอน: f(x 1 , x 2, x n) = (อาจ = อาจิ)

เมทริกซ์ A ที่ประกอบด้วยสัมประสิทธิ์เหล่านี้เรียกว่า เมทริกซ์รูปแบบกำลังสอง ก็เสมอกัน สมมาตรเมทริกซ์ (เช่น เมทริกซ์สมมาตรเกี่ยวกับเส้นทแยงมุมหลัก a ij = a ji)

ในรูปแบบเมทริกซ์ รูปแบบกำลังสองคือ f(X) = X T AX โดยที่

อย่างแท้จริง

ตัวอย่างเช่น ลองเขียนรูปกำลังสองในรูปแบบเมทริกซ์

เมื่อต้องการทำเช่นนี้ เราจะหาเมทริกซ์ที่มีรูปแบบกำลังสอง องค์ประกอบในแนวทแยงจะเท่ากับค่าสัมประสิทธิ์ของตัวแปรกำลังสอง และองค์ประกอบที่เหลือจะเท่ากับครึ่งหนึ่งของสัมประสิทธิ์ที่สอดคล้องกันของรูปแบบกำลังสอง นั่นเป็นเหตุผล

ปล่อยให้เมทริกซ์คอลัมน์ของตัวแปร X ได้รับจากการแปลงเชิงเส้นที่ไม่เสื่อมของเมทริกซ์คอลัมน์ Y เช่น X = CY โดยที่ C คือเมทริกซ์ที่ไม่เอกพจน์ในลำดับที่ n จากนั้นรูปแบบกำลังสอง f(X) = X T AX = (CY) T A(CY) = (Y T C T)A(CY) = Y T (C T AC)Y

ดังนั้น ด้วยการแปลงเชิงเส้นที่ไม่เสื่อมลง C เมทริกซ์ของรูปแบบกำลังสองจึงมีรูปแบบ: A * = C T AC

ตัวอย่างเช่น ลองหารูปแบบกำลังสอง f(y 1, y 2) ซึ่งได้จากรูปแบบกำลังสอง f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 โดยการแปลงเชิงเส้น

รูปทรงกำลังสองเรียกว่า ตามบัญญัติ(มี มุมมองที่เป็นที่ยอมรับ) ถ้าค่าสัมประสิทธิ์ทั้งหมด a ij = 0 สำหรับ i ≠ j เช่น
f(x 1, x 2, x n) = a 11 x 1 2 + a 22 x 2 2 + a nn x n 2 =

เมทริกซ์ของมันคือเส้นทแยงมุม

ทฤษฎีบท(ไม่ได้ให้หลักฐานที่นี่) รูปแบบกำลังสองใดๆ สามารถถูกลดให้เป็นรูปแบบมาตรฐานได้โดยใช้การแปลงเชิงเส้นที่ไม่เสื่อมลง

ตัวอย่างเช่น ขอให้เราลดรูปแบบกำลังสองให้เป็นรูปแบบมาตรฐาน
ฉ(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3

เมื่อต้องการทำสิ่งนี้ ขั้นแรกให้เลือกกำลังสองที่สมบูรณ์ด้วยตัวแปร x 1:

ฉ(x 1, x 2, x 3) = 2(x 1 2 + 2x 1 x 2 + x 2 2) - 2x 2 2 - 3x 2 2 - x 2 x 3 = 2(x 1 + x 2) 2 - 5x 2 2 - x 2 x 3

ตอนนี้เราเลือกกำลังสองที่สมบูรณ์ด้วยตัวแปร x 2:

ฉ(x 1, x 2, x 3) = 2(x 1 + x 2) 2 - 5(x 2 2 + 2* x 2 *(1/10)x 3 + (1/100)x 3 2) + (5/100)x 3 2 =
= 2(x 1 + x 2) 2 - 5(x 2 - (1/10)x 3) 2 + (1/20)x 3 2.

จากนั้นการแปลงเชิงเส้นที่ไม่เสื่อมลง y 1 = x 1 + x 2, y 2 = x 2 + (1/10)x 3 และ y 3 = x 3 นำรูปแบบกำลังสองนี้มาสู่รูปแบบมาตรฐาน f(y 1, y 2 , ปี 3) = 2ปี 1 2 - 5ปี 2 2 + (1/20)ปี 3 2 .

โปรดทราบว่ารูปแบบมาตรฐานของรูปแบบกำลังสองถูกกำหนดไว้อย่างคลุมเครือ (รูปแบบกำลังสองเดียวกันสามารถลดเป็นรูปแบบมาตรฐานในรูปแบบบัญญัติได้หลายวิธี) อย่างไรก็ตามได้รับ ในรูปแบบต่างๆรูปแบบบัญญัติมีคุณสมบัติทั่วไปหลายประการ โดยเฉพาะอย่างยิ่ง จำนวนพจน์ที่มีค่าสัมประสิทธิ์บวก (ลบ) ของรูปแบบกำลังสองไม่ได้ขึ้นอยู่กับวิธีการลดรูปแบบให้อยู่ในรูปแบบนี้ (ตัวอย่างเช่น ในตัวอย่างที่พิจารณาว่าจะมีค่าสัมประสิทธิ์ลบสองค่าและค่าบวกหนึ่งค่าเสมอ) คุณสมบัตินี้เรียกว่ากฎความเฉื่อยของรูปแบบกำลังสอง

ขอให้เราตรวจสอบสิ่งนี้โดยนำรูปแบบกำลังสองเดียวกันมาสู่รูปแบบมาตรฐานในรูปแบบที่ต่างออกไป มาเริ่มการแปลงด้วยตัวแปร x 2:

ฉ(x 1, x 2, x 3) = 2x 1 2 + 4x 1 x 2 - 3x 2 2 - x 2 x 3 = -3x 2 2 - x 2 x 3 + 4x 1 x 2 + 2x 1 2 = - 3(x 2 2 +
+ 2* x 2 ((1/6) x 3 - (2/3)x 1) + ((1/6) x 3 - (2/3)x 1) 2) + 3((1/6) x 3 - (2/3)x 1) 2 + 2x 1 2 =
= -3(x 2 + (1/6) x 3 - (2/3)x 1) 2 + 3((1/6) x 3 + (2/3)x 1) 2 + 2x 1 2 = f (ปี 1 , ปี 2 , ปี 3) = -3ปี 1 2 -
+3y 2 2 + 2y 3 2 โดยที่ y 1 = - (2/3)x 1 + x 2 + (1/6) x 3, y 2 = (2/3)x 1 + (1/6) x 3 และ y 3 = x 1 . ที่นี่มีค่าสัมประสิทธิ์ลบ -3 ที่ y 1 และค่าสัมประสิทธิ์บวกสองตัว 3 และ 2 ที่ y 2 และ y 3 (และเมื่อใช้วิธีอื่นเราจะได้ค่าสัมประสิทธิ์ลบ (-5) ที่ y 2 และค่าบวกสองตัว: 2 ที่ y 1 และ 1/20 ที่ y 3)

ควรสังเกตด้วยว่าอันดับของเมทริกซ์รูปแบบกำลังสองเรียกว่า อันดับของรูปแบบกำลังสองเท่ากับจำนวนสัมประสิทธิ์ที่ไม่ใช่ศูนย์ของรูปแบบมาตรฐานและไม่เปลี่ยนแปลงภายใต้การแปลงเชิงเส้น

รูปแบบกำลังสอง f(X) เรียกว่า ในเชิงบวก (เชิงลบ) แน่ใจถ้าสำหรับค่าทั้งหมดของตัวแปรที่ไม่เท่ากับศูนย์พร้อมกันจะเป็นค่าบวกนั่นคือ f(X) > 0 (ลบ เช่น
ฉ(เอ็กซ์)< 0).

ตัวอย่างเช่น รูปกำลังสอง f 1 (X) = x 1 2 + x 2 2 เป็นค่าแน่นอนที่เป็นบวก เนื่องจาก คือผลรวมของกำลังสอง และรูปแบบกำลังสอง f 2 (X) = -x 1 2 + 2x 1 x 2 - x 2 2 เป็นค่าแน่นอนที่เป็นลบ เนื่องจาก แสดงว่าสามารถแสดงเป็น f 2 (X) = -(x 1 - x 2) 2

ในสถานการณ์จริงส่วนใหญ่ การสร้างเครื่องหมายที่แน่นอนของรูปกำลังสองจะยากกว่า ดังนั้นในกรณีนี้เราใช้ทฤษฎีบทใดทฤษฎีหนึ่งต่อไปนี้ (เราจะกำหนดโดยไม่ต้องพิสูจน์)

ทฤษฎีบท- รูปแบบกำลังสองเป็นบวก (ลบ) แน่นอนหากค่าลักษณะเฉพาะทั้งหมดของเมทริกซ์เป็นบวก (ลบ)

ทฤษฎีบท(เกณฑ์ซิลเวสเตอร์) รูปแบบกำลังสองเป็นบวกแน่นอนก็ต่อเมื่อค่ารองนำหน้าทั้งหมดของเมทริกซ์ในรูปแบบนี้เป็นบวกเท่านั้น

หลัก (มุม) ผู้เยาว์เมทริกซ์ลำดับที่ k ของเมทริกซ์ A ของลำดับที่ n เรียกว่าดีเทอร์มิแนนต์ของเมทริกซ์ ซึ่งประกอบด้วย k แถวและคอลัมน์แรกของเมทริกซ์ A ()

โปรดทราบว่าสำหรับรูปกำลังสองแน่นอนที่เป็นลบ เครื่องหมายของตัวรองหลักจะสลับกัน และตัวรองอันดับแรกต้องเป็นค่าลบ

ตัวอย่างเช่น ลองตรวจสอบรูปแบบกำลังสอง f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 + 3x 2 2 เพื่อดูความแน่นอนของเครื่องหมาย

= (2 - ลิตร)*
*(3 - ลิตร) - 4 = (6 - 2l - 3l + l 2) - 4 = l 2 - 5l + 2 = 0; ง = 25 - 8 = 17;
- ดังนั้นรูปกำลังสองจึงเป็นค่าแน่นอนที่เป็นบวก

วิธีที่ 2 Principal minor ของลำดับแรกของเมทริกซ์ A D 1 = a 11 = 2 > 0 Principal minor ของลำดับที่สอง D 2 = = 6 - 4 = 2 > 0 ดังนั้น ตามเกณฑ์ของ Sylvester รูปกำลังสองคือ บวกแน่นอน

เราตรวจสอบรูปแบบกำลังสองอีกรูปแบบหนึ่งเพื่อหาค่าแน่นอนของเครื่องหมาย f(x 1, x 2) = -2x 1 2 + 4x 1 x 2 - 3x 2 2

วิธีที่ 1 มาสร้างเมทริกซ์กำลังสองรูปแบบ A = กันดีกว่า สมการคุณลักษณะจะมีรูปแบบ = (-2 - ลิตร)*
*(-3 - ลิตร) - 4 = (6 + 2l + 3l + l 2) - 4 = l 2 + 5l + 2 = 0; ง = 25 - 8 = 17;
- ดังนั้นรูปกำลังสองจึงเป็นค่าแน่นอนเชิงลบ

วิธีที่ 2 หลักของเมทริกซ์ลำดับแรกของเมทริกซ์ A D 1 = a 11 =
= -2 < 0. Главный минор второго порядка D 2 = = 6 - 4 = 2 >0. ดังนั้น ตามเกณฑ์ของซิลเวสเตอร์ รูปแบบกำลังสองจึงเป็นค่าแน่นอนเชิงลบ (สัญญาณของผู้เยาว์หลักสลับกัน โดยเริ่มจากเครื่องหมายลบ)

และอีกตัวอย่างหนึ่ง เราจะตรวจสอบรูปแบบกำลังสองที่กำหนดเครื่องหมาย f(x 1, x 2) = 2x 1 2 + 4x 1 x 2 - 3x 2 2

วิธีที่ 1 มาสร้างเมทริกซ์กำลังสองรูปแบบ A = กันดีกว่า สมการคุณลักษณะจะมีรูปแบบ = (2 - ลิตร)*
*(-3 - ลิตร) - 4 = (-6 - 2l + 3l + l 2) - 4 = l 2 + l - 10 = 0; ง = 1 + 40 = 41;
.

หนึ่งในจำนวนเหล่านี้เป็นลบและอีกจำนวนหนึ่งเป็นค่าบวก สัญญาณของค่าลักษณะเฉพาะนั้นแตกต่างกัน ดังนั้น รูปแบบกำลังสองไม่สามารถเป็นได้ทั้งค่าลบหรือค่าบวกที่แน่นอน กล่าวคือ รูปแบบกำลังสองนี้ไม่มีเครื่องหมายที่แน่นอน (สามารถรับค่าของเครื่องหมายใดก็ได้)

วิธีที่ 2. Principal minor ของลำดับที่ 1 ของเมทริกซ์ A D 1 = a 11 = 2 > 0. Principal minor ของลำดับที่ 2 D 2 = = -6 - 4 = -10< 0. Следовательно, по критерию Сильвестра квадратичная форма не является знакоопределенной (знаки главных миноров разные, при этом первый из них - положителен).

คำนิยาม 9.3เวกเตอร์ เอ็กซ์ เรียกว่า eigenvectorเมทริกซ์ กถ้ามีตัวเลขดังกล่าว λ, ที่มีความเท่าเทียมกัน: ก เอ็กซ์= λ เอ็กซ์, นั่นคือผลของการสมัคร เอ็กซ์ การแปลงเชิงเส้นที่ระบุโดยเมทริกซ์ ก, คือการคูณเวกเตอร์นี้ด้วยตัวเลข λ - เบอร์นั้นเอง λ เรียกว่า ค่าลักษณะเฉพาะเมทริกซ์ ก.

แทนลงในสูตร (9.3) x` เจ = แลม x เจ ,เราได้รับระบบสมการในการกำหนดพิกัดของเวกเตอร์ลักษณะเฉพาะ:

. (9.5)

เชิงเส้นนี้ ระบบที่เป็นเนื้อเดียวกันจะมีวิธีแก้ปัญหาที่ไม่ซับซ้อนก็ต่อเมื่อปัจจัยกำหนดหลักคือ 0 (กฎของแครเมอร์) โดยเขียนเงื่อนไขนี้ในรูปแบบ:

เราได้รับสมการในการกำหนดค่าลักษณะเฉพาะ λ , เรียกว่า สมการลักษณะเฉพาะ- สามารถแสดงโดยย่อได้ดังนี้:

| เอ - เลอี | = 0, (9.6)

เนื่องจากด้านซ้ายมีดีเทอร์มิแนนต์ของเมทริกซ์ เอ-เลอี- ญาติพหุนาม แล | เอ - เลอี- เรียกว่า พหุนามลักษณะเฉพาะเมทริกซ์ A

คุณสมบัติของพหุนามคุณลักษณะ:

1) พหุนามคุณลักษณะของการแปลงเชิงเส้นไม่ได้ขึ้นอยู่กับการเลือกพื้นฐาน การพิสูจน์. (ดู (9.4)) แต่ เพราะฉะนั้น, . จึงไม่ขึ้นอยู่กับการเลือกพื้นฐาน ซึ่งหมายความว่า | เอ-เลอี- ไม่เปลี่ยนแปลงเมื่อย้ายไปยังพื้นฐานใหม่

2) ถ้าเป็นเมทริกซ์ กการแปลงเชิงเส้นคือ สมมาตร(เหล่านั้น. และ อิจ = อา จิ) จากนั้นรากทั้งหมดของสมการคุณลักษณะ (9.6) จะเป็นจำนวนจริง

คุณสมบัติของค่าลักษณะเฉพาะและเวกเตอร์ลักษณะเฉพาะ:

1) หากคุณเลือกพื้นฐานจากเวกเตอร์ลักษณะเฉพาะ x 1, x 2, x 3 ซึ่งสอดคล้องกับค่าลักษณะเฉพาะ แล 1, แล 2, แล 3เมทริกซ์ กจากนั้นบนพื้นฐานนี้ การแปลงเชิงเส้น A มีเมทริกซ์ที่มีรูปแบบแนวทแยง:

(9.7) การพิสูจน์คุณสมบัตินี้เป็นไปตามคำจำกัดความของเวกเตอร์ลักษณะเฉพาะ

2) ถ้าค่าลักษณะเฉพาะของการเปลี่ยนแปลง กต่างกัน ดังนั้นเวกเตอร์ลักษณะเฉพาะที่สอดคล้องกันของพวกมันจะเป็นอิสระเชิงเส้นตรง

3) ถ้าพหุนามลักษณะเฉพาะของเมทริกซ์ กมีรากที่แตกต่างกันสามราก แล้วมีพื้นฐานบางอย่างคือเมทริกซ์ กมีลักษณะเป็นแนวทแยง

มาหาค่าลักษณะเฉพาะและเวกเตอร์ลักษณะเฉพาะของเมทริกซ์ มาสร้างสมการลักษณะเฉพาะกัน: (1- λ )(5 - λ )(1 - λ ) + 6 - 9(5 - λ ) - (1 - λ ) - (1 - λ ) = 0, λ ลูกบาศก์ - 7 λ ² + 36 = 0, λ 1 = -2, λ 2 = 3, λ 3 = 6.

มาหาพิกัดของเวกเตอร์ลักษณะเฉพาะที่สอดคล้องกับแต่ละค่าที่พบ λ. จาก (9.5) จะได้ว่า ถ้า เอ็กซ์ (1) ={x 1 ,x 2 ,x 3) – eigenvector ที่สอดคล้องกัน λ 1 =-2 แล้ว

- ระบบสหกรณ์แต่ไม่แน่นอน สารละลายของมันสามารถเขียนได้ในรูป เอ็กซ์ (1) ={ก,0,-ก) โดยที่ a คือตัวเลขใดๆ โดยเฉพาะอย่างยิ่งหากเราต้องการสิ่งนั้น | x (1) |=1, เอ็กซ์ (1) =

การทดแทนเข้าสู่ระบบ (9.5) λ 2 =3 เราได้รับระบบสำหรับกำหนดพิกัดของเวกเตอร์ลักษณะเฉพาะที่สอง - x (2) ={ปีที่ 1 ,ปีที่ 2 ,ปีที่ 3}:

, ที่ไหน เอ็กซ์ (2) ={ข,-ข,ข) หรือระบุ | x (2) |=1, x (2) =

สำหรับ λ 3 = 6 จงหาเวกเตอร์ลักษณะเฉพาะ x (3) ={ซี 1 , ซี 2 , ซี 3}:

, x (3) ={ค,2ค,ค) หรือในเวอร์ชันมาตรฐาน

เอ็กซ์ (3) = สังเกตได้เลยว่า เอ็กซ์ (1) เอ็กซ์ (2) = ab–ab= 0, x (1) x (3) = เอซี-เอซี= 0, x (2) x (3) = ก่อนคริสต์ศักราช- 2บีซี + บีซี= 0 ดังนั้น เวกเตอร์ลักษณะเฉพาะของเมทริกซ์นี้จึงตั้งฉากเป็นคู่

บรรยายครั้งที่ 10.

รูปแบบกำลังสองและการเชื่อมต่อกับเมทริกซ์สมมาตร คุณสมบัติของเวกเตอร์ลักษณะเฉพาะและค่าลักษณะเฉพาะของเมทริกซ์สมมาตร การลดรูปแบบกำลังสองให้เป็นรูปแบบมาตรฐาน

คำจำกัดความ 10.1รูปร่างกำลังสองตัวแปรจริง x 1, x 2,…, xnเรียกว่าพหุนามของดีกรีที่สองในตัวแปรเหล่านี้ซึ่งไม่มีเทอมอิสระและเทอมของดีกรีแรก

ตัวอย่างของรูปแบบกำลังสอง:

(n = 2),

(n = 3). (10.1)

ให้เรานึกถึงคำจำกัดความของเมทริกซ์สมมาตรที่ให้ไว้ในการบรรยายครั้งล่าสุด:

คำจำกัดความ 10.2เรียกว่าเมทริกซ์จตุรัส สมมาตรถ้า นั่นคือถ้าองค์ประกอบเมทริกซ์ที่มีความสมมาตรเกี่ยวกับเส้นทแยงมุมหลักเท่ากัน

คุณสมบัติของค่าลักษณะเฉพาะและเวกเตอร์ลักษณะเฉพาะของเมทริกซ์สมมาตร:

1) ค่าลักษณะเฉพาะทั้งหมดของเมทริกซ์สมมาตรนั้นเป็นค่าจริง

หลักฐาน (สำหรับ n = 2).

ปล่อยให้เมทริกซ์ กมีรูปแบบ: - มาสร้างสมการลักษณะเฉพาะกัน:

(10.2) เรามาค้นหาผู้จำแนก:

ดังนั้นสมการจึงมีรากจริงเท่านั้น

2) เวกเตอร์ลักษณะเฉพาะของเมทริกซ์สมมาตรนั้นตั้งฉาก

หลักฐาน (สำหรับ n= 2).

พิกัดของเวกเตอร์ลักษณะเฉพาะและจะต้องเป็นไปตามสมการ