Mathematical game theory. Examples of recording and solving games from life
Game theory - a set of mathematical methods for resolving conflict situations (conflicts of interests). In game theory, a game is called mathematical model of a conflict situation. Item special interest game theory - the study of decision-making strategies of game participants under conditions of uncertainty. Uncertainty stems from the fact that two or more parties pursue opposing goals, and the results of any action of each party depend on the moves of the partner. At the same time, each party strives to make optimal decisions that realize the set goals to the greatest extent.
Game theory is most consistently applied in economics, where conflict situations arise, for example, in the relationship between supplier and consumer, buyer and seller, bank and client. The application of game theory can also be found in politics, sociology, biology, and military art.
From the history of game theory
History of game theory as an independent discipline began in 1944, when John von Neumann and Oscar Morgenstern published the book “The Theory of Games and Economic Behavior”. Although examples of game theory have been encountered before: the treatise of the Babylonian Talmud on the division of the property of a deceased husband between his wives, card games in the 18th century, the development of the theory of chess at the beginning of the 20th century, the proof of the minimax theorem of the same John von Neumann in 1928 year, without which there would be no game theory.
In the 50s of the 20th century, Melvin Drescher and Meryl Flood from Rand Corporation John Nash, the first to experimentally apply the prisoner's dilemma, developed the concept of Nash equilibrium in his works on the state of equilibrium in two-person games.
Reinhard Salten published the book "The Treatment of Oligopoly in Game Theory on Demand" ("Spieltheoretische Behandlung eines Oligomodells mit Nachfrageträgheit") in 1965, with which the application of game theory in economics received a new driving force. A step forward in the evolution of game theory is associated with the work of John Maynard Smith, “Evolutionary Stable Strategy” (1974). The prisoner's dilemma was popularized in Robert Axelrod's 1984 book The Evolution of Cooperation. In 1994, John Nash, John Harsanyi and Reinhard Selten were awarded the Nobel Prize for their contributions to game theory.
Game theory in life and business
Let us dwell in more detail on the essence of a conflict situation (clash of interests) in the sense as it is understood in game theory for further modeling of various situations in life and business. Let an individual be in a position that leads to one of several possible outcomes, and the individual has some personal preferences regarding these outcomes. But although he can to some extent control the variables that determine the outcome, he does not have complete power over them. Sometimes control is in the hands of several individuals who, like him, have some preferences in relation to possible outcomes, but in general case the interests of these individuals are not aligned. In other cases, the final outcome may depend both on chance (sometimes called natural disasters in legal science) and on other individuals. Game theory systematizes observations of such situations and formulations general principles to guide reasonable actions in such situations.
In some respects, the name "game theory" is unfortunate, since it suggests that game theory considers only those who do not have social significance collisions that occur in parlor games, but still this theory has a much broader meaning.
The following economic situation can give an idea of the application of game theory. Suppose there are several entrepreneurs, each of whom strives to obtain maximum profit, while having only limited power over the variables that determine this profit. An entrepreneur has no power over variables that another entrepreneur controls, but which can greatly influence the income of the first. Treating this situation as a game may raise the following objection. In the game model, it is assumed that each entrepreneur makes one choice from the range of possible choices, and these single choices determine profits. Obviously, this almost cannot happen in reality, since in this case complex management apparatuses would not be needed in industry. There are simply a number of decisions and modifications of these decisions that depend on the choices made by other participants economic system(by players). But in principle one can imagine some administrator anticipating all possible contingencies and detailing the action to be taken in each case, rather than solving each problem as it arises.
A military conflict, by definition, is a clash of interests in which neither side has complete control over the variables that determine the outcome, which is decided by a series of battles. You can simply consider the outcome to be a win or a loss and assign the numerical values 1 and 0 to them.
One of the simplest conflict situations that can be written down and resolved in game theory is a duel, which is a conflict between two players 1 and 2, having respectively p And q shots. For each player there is a function indicating the probability that the player's shot i at a point in time t will give a hit that will be fatal.
As a result, game theory comes to the following formulation of a certain class of conflicts of interests: there are n players, and each needs to choose one option from a hundred specific set, and when making a choice, the player has no information about the choices of other players. The player's possible choice area may contain elements such as "move the ace of spades", "produce tanks instead of cars", or in a general sense, a strategy that defines all the actions that need to be taken in all possible circumstances. Each player is faced with a task: what choice should he make so that his private influence on the outcome brings him the greatest possible win?
Mathematical model in game theory and formalization of problems
As we have already noted, the game is a mathematical model of a conflict situation and requires the following components:
- interested parties;
- possible actions on each side;
- interests of the parties.
The parties interested in the game are called players , each of them can take at least two actions (if the player has only one action at his disposal, then he does not actually participate in the game, since it is known in advance what he will take). The outcome of the game is called winning .
A real conflict situation is not always, but the game (in the concept of game theory) always proceeds according to certain rules , which precisely determine:
- options for players' actions;
- the amount of information each player has about their partner’s behavior;
- the payoff that each set of actions leads to.
Examples of formalized games include football, card games, and chess.
But in economics, a model of player behavior arises, for example, when several firms strive to take a more advantageous place in the market, several individuals try to divide some good (resources, finances) among themselves so that everyone gets as much as possible. Players in conflict situations in the economy, which can be modeled as a game, are firms, banks, individuals and other economic agents. In turn, in war conditions, the game model is used, for example, in choosing more best weapons(from existing or potential) to defeat the enemy or protect against attack.
The game is characterized by uncertainty of the outcome . The reasons for uncertainty can be divided into the following groups:
- combinatorial (as in chess);
- the influence of random factors (as in the game "heads or tails", dice, card games);
- strategic (the player does not know what action the enemy will take).
Player strategy is a set of rules that determine his actions at each move depending on the current situation.
The purpose of game theory is to determine the optimal strategy for each player. Determining such a strategy means solving the game. Optimality of strategy is achieved when one of the players should get the maximum win, while the second one sticks to his strategy. And the second player should have a minimal loss if the first one sticks to his strategy.
Classification of games
- Classification by number of players (game of two or more persons). Two-person games occupy a central place in all game theory. The core concept of game theory for two-person games is a generalization of the very significant idea of equilibrium that naturally appears in two-person games. As for games n individuals, then one part of game theory is devoted to games in which cooperation between players is prohibited. In another part of game theory n individuals assume that players can cooperate for mutual benefit (see later in this paragraph on non-cooperative and cooperative games).
- Classification by the number of players and their strategies (the number of strategies is at least two, may be infinity).
- Classification by amount of information relative to past moves: games with complete information and incomplete information. Let there be player 1 - buyer and player 2 - seller. If player 1 does not have complete information about the actions of player 2, then player 1 may not distinguish between the two alternatives between which he must make a choice. For example, choosing between two types of some product and not knowing that, according to some characteristics, the product A worse product B, player 1 may not see the difference between the alternatives.
- Classification according to the principles of division of winnings : cooperative, coalition on the one hand and non-cooperative, non-coalition on the other hand. IN non-cooperative game , or otherwise - non-cooperative game , players choose strategies simultaneously without knowing which strategy the second player will choose. Communication between players is impossible. IN cooperative game , or otherwise - coalition game , players can form coalitions and take collective actions to increase their winnings.
- Finite two-person zero-sum game or an antagonistic game is strategy game with full information, which involves parties with opposing interests. Antagonistic games are matrix games .
A classic example from game theory is the prisoner's dilemma.
The two suspects are taken into custody and separated from each other. The district attorney is convinced that they committed a serious crime, but does not have enough evidence to charge them at trial. He tells each prisoner that he has two alternatives: confess to the crime the police believe he committed, or not confess. If both don't confess, the DA will charge them with some minor crime, such as petty theft or illegal possession of a weapon, and they will both receive a small sentence. If they both confess, they will be subject to prosecution, but he will not demand the harshest sentence. If one confesses and the other does not, then the one who confessed will have his sentence commuted for extraditing an accomplice, while the one who persists will receive “to the fullest.”
If this strategic task is formulated in terms of conclusion, then it boils down to the following:
Thus, if both prisoners do not confess, they will receive 1 year each. If both confess, each will receive 8 years. And if one confesses, the other does not confess, then the one who confessed will get off with three months in prison, and the one who does not confess will receive 10 years. The above matrix correctly reflects the prisoner's dilemma: everyone is faced with the question of whether to confess or not to confess. The game that the district attorney offers to the prisoners is non-cooperative game or otherwise - non-cooperative game . If both prisoners had the opportunity to cooperate (i.e. the game would be co-op or else coalition game ), then both would not confess and would receive a year in prison each.
Examples of using mathematical tools of game theory
We now move on to consider solutions to examples of common classes of games, for which there are research and solution methods in game theory.
An example of formalization of a non-cooperative (non-cooperative) game of two persons
In the previous paragraph, we already looked at an example of a non-cooperative (non-cooperative) game (prisoner's dilemma). Let's strengthen our skills. A classic plot inspired by “The Adventures of Sherlock Holmes” by Arthur Conan Doyle is also suitable for this. One can, of course, object: the example is not from life, but from literature, but Conan Doyle has not established himself as a science fiction writer! Classic also because the task was completed by Oskar Morgenstern, as we have already established, one of the founders of game theory.
Example 1. An abbreviated summary of a fragment of one of “The Adventures of Sherlock Holmes” will be given. According to the well-known concepts of game theory, create a model of a conflict situation and formally write down the game.
Sherlock Holmes intends to travel from London to Dover with the further goal of getting to the continent (European) in order to escape from Professor Moriarty, who is pursuing him. Having boarded the train, he saw Professor Moriarty on the station platform. Sherlock Holmes admits that Moriarty can choose a special train and overtake it. Sherlock Holmes has two alternatives: continue the journey to Dover or get off at Canterbury station, which is the only intermediate station on his route. We accept that his opponent is intelligent enough to determine Holmes' capabilities, so he has the same two alternatives. Both opponents must choose a station to get off the train at, without knowing what decision each of them will make. If, as a result of making a decision, both end up at the same station, then we can definitely assume that Sherlock Holmes will be killed by Professor Moriarty. If Sherlock Holmes reaches Dover safely, he will be saved.
Solution. We can consider Conan Doyle's heroes as participants in the game, that is, players. Available to every player i (i=1,2) two pure strategies:
- get off at Dover (strategy si1 ( i=1,2) );
- get off at an intermediate station (strategy si2 ( i=1,2) )
Depending on which of the two strategies each of the two players chooses, a special combination of strategies will be created as a pair s = (s1 , s 2 ) .
Each combination can be associated with an event - the outcome of the attempted murder of Sherlock Holmes by Professor Moriarty. We create a matrix of this game with possible events.
Under each of the events there is an index indicating the acquisition of Professor Moriarty, and calculated depending on the salvation of Holmes. Both heroes choose a strategy at the same time, not knowing what the enemy will choose. Thus, the game is non-cooperative because, firstly, the players are on different trains, and secondly, they have opposing interests.
An example of formalization and solution of a cooperative (coalition) game n persons
At this point, the practical part, that is, the process of solving an example problem, will be preceded by a theoretical part, in which we will get acquainted with the concepts of game theory for solving cooperative (non-cooperative) games. For this task, game theory suggests:
- characteristic function (to put it simply, it reflects the magnitude of the benefit of uniting players into a coalition);
- the concept of additivity (the property of quantities, consisting in the fact that the value of a quantity corresponding to the whole object is equal to the sum of the values of quantities corresponding to its parts in a certain class of partitions of the object into parts) and superadditivity (the value of a quantity corresponding to the whole object is greater than the sum of the values of quantities, corresponding to its parts) of the characteristic function.
The superadditivity of the characteristic function suggests that joining a coalition is beneficial to the players, since in this case the value of the coalition's payoff increases with the number of players.
To formalize the game, we need to introduce formal notations for the above concepts.
For Game n let us denote the set of all its players as N= (1,2,...,n) Any non-empty subset of the set N let's denote it as T(including itself N and all subsets consisting of one element). There is a lesson on the site " Sets and operations on sets", which opens in a new window when you click on the link.
The characteristic function is denoted as v and its domain of definition consists of possible subsets of the set N. v(T) - the value of the characteristic function for a particular subset, for example, the income received by a coalition, possibly including one consisting of one player. This is important because game theory requires checking the presence of superadditivity for the values of the characteristic function of all disjoint coalitions.
For two non-empty subset coalitions T1 And T2 The additivity of the characteristic function of a cooperative (coalition) game is written as follows:
And superadditivity is like this:
Example 2. Three music school students work part-time in different clubs; they receive their income from club visitors. Determine whether it is profitable for them to join forces (if so, under what conditions), using the concepts of game theory to solve cooperative games n persons, with the following initial data.
On average, their revenue per evening was:
- the violinist has 600 units;
- the guitarist has 700 units;
- the singer has 900 units.
In an attempt to increase revenue, students created various groups over the course of several months. The results showed that by teaming up, they could increase their evening revenue by:
- violinist + guitarist earned 1500 units;
- violinist + singer earned 1800 units;
- guitarist + singer earned 1900 units;
- violinist + guitarist + singer earned 3000 units.
Solution. In this example, the number of players in the game n= 3, therefore, the domain of definition of the characteristic function of the game consists of 2³ = 8 possible subsets of the set of all players. Let us list all possible coalitions T:
- coalitions of one element, each of which consists of one player - a musician: T{1} , T{2} , T{3} ;
- coalition of two elements: T{1,2} , T{1,3} , T{2,3} ;
- coalition of three elements: T{1,2,3} .
We will assign a serial number to each player:
- violinist - 1st player;
- guitarist - 2nd player;
- singer - 3rd player.
Based on the problem data, we determine the characteristic function of the game v:
v(T(1)) = 600 ; v(T(2)) = 700 ; v(T(3)) = 900 ; these values of the characteristic function are determined based on the payoffs of the first, second and third players, respectively, when they do not unite in a coalition;
v(T(1,2)) = 1500 ; v(T(1,3)) = 1800 ; v(T(2,3)) = 1900 ; these values of the characteristic function are determined by the revenue of each pair of players united in a coalition;
v(T(1,2,3)) = 3000 ; this value of the characteristic function is determined by the average revenue in the case when the players united in threes.
Thus, we have listed all possible coalitions of players; there are eight of them, as it should be, since the domain of definition of the characteristic function of the game consists of exactly eight possible subsets of the set of all players. This is what game theory requires, since we need to check the presence of superadditivity for the values of the characteristic function of all disjoint coalitions.
How are the superadditivity conditions satisfied in this example? Let's determine how players form disjoint coalitions T1 And T2 . If some players are part of a coalition T1 , then all other players are part of the coalition T2 and by definition, this coalition is formed as the difference of the entire set of players and the set T1 . Then if T1 - a coalition of one player, then in a coalition T2 there will be second and third players if in a coalition T1 there will be the first and third players, then the coalition T2 will consist of only the second player, and so on.
Game theory as a branch of operations research, it is a theory mathematical models making optimal decisions in conditions of uncertainty or conflict of several parties with different interests. Game theory studies optimal strategies in gaming situations. These include situations related to the selection of the most advantageous production solutions for a system of scientific and economic experiments, the organization of statistical control, and economic relations between industrial enterprises and other sectors. Formalizing conflict situations mathematically, they can be represented as a game of two, three, etc. players, each of whom pursues the goal of maximizing their benefit, their winnings at the expense of the other.The "Game Theory" section is represented by three online calculators:
- Optimal strategies of players. In such problems, a payment matrix is specified. Need to find clean or mixed strategies players and game price. To solve, you must specify the dimension of the matrix and the solution method. The service implements the following methods for solving a two-player game:
- Minimax. If you need to find the players' pure strategy or answer a question about the saddle point of a game, choose this solution method.
- Simplex method. Used to solve mixed strategy games using methods linear programming.
- Graphic method. Used to solve mixed strategy games. If there is a saddle point, the solution stops. Example: For a given payment matrix, find the optimal mixed strategies of players and the price of the game using graphic method game solutions.
- Brown-Robinson iterative method. The iterative method is used when the graphical method is not applicable and when the algebraic and matrix methods. This method gives an approximate value of the price of the game, and the true value can be obtained with any desired degree of accuracy. This method is not sufficient for finding optimal strategies, but it allows you to track the dynamics of a turn-based game and determine the cost of the game for each player at each step.
All methods use a check for dominant rows and columns. - Bimatrix game. Usually in such a game two matrices of the same size of payoffs of the first and second players are specified. The rows of these matrices correspond to the strategies of the first player, and the columns of the matrices correspond to the strategies of the second player. In this case, the first matrix represents the winnings of the first player, and the second matrix represents the winnings of the second.
- Games with nature. It is used when it is necessary to select a management decision according to the criteria of Maximax, Bayes, Laplace, Wald, Savage, Hurwitz.
For the Bayes criterion, it will also be necessary to enter the probabilities of events occurring. If they are not specified, leave the default values (there will be equivalent events).
For the Hurwitz criterion, indicate the level of optimism λ. If this parameter is not specified in the conditions, you can use the values 0, 0.5 and 1.
Many problems require finding solutions using computers. The above services and functions are one of the tools.
Solving a matrix game using a graphical method
Solving a matrix game using linear programming methods
- Matrix game. Using the simplex method. We find the guaranteed payoff determined by the lower price of the game a = max(a i) = 2, which indicates the maximum pure strategy A 1 .
- An example of solving a matrix game using the linear programming method. Solve a matrix game using linear programming.
Give a graphical representation, reduce to normal form and find the exact solution of a positional game with the following payoff function:
Player A makes the 1st move: he chooses number x from a set of two numbers.
The 2nd move is made by player B: not knowing about the choice of player A on the 1st move, he chooses the number y from the set of two numbers.
The 3rd move is made by player A: he chooses the number z from a set of two numbers, knowing the values of y chosen by player B on the 2nd move, but not remembering his own choice of x on the 1st move.
Games with nature
- Statistical games
An agricultural enterprise can sell some products:
A1) immediately after cleaning;
A2) in the winter months;
A3) in the spring months.
Profit depends on the selling price in a given period of time, storage costs and possible losses. The amount of profit calculated for different states-ratios of income and costs (S1, S2 and S3), during the entire period of implementation, is presented in the form of a matrix (million rubles) - The company produces dresses and suits, the sale of which depends on weather conditions. The company's costs per unit of production during April-May will be...
- Solving the problem of raw material reserves. Over a certain period of time at the enterprise, the consumption of raw materials, depending on its quality, is 1, 2, 3 and 4.
- Strategies of extreme pessimism, extreme optimism and optimism-pessimism
Bimatrix games
Decision tree in game theory (an example of solving a problem).
see also a collection of solutions on game theory (solving matrix games), typical problems on EMM (linear programming, game theory).
There are three television companies operating in the city: ABC, СВS And NBC. These companies may begin their evening news program at 6:30 or 7:00. 60% of TV viewers prefer to watch the evening news at 6.30, and 40% prefer to watch the evening news at 7.00. The company's most popular evening news program ABC, the least popular are news prepared by the company NBC. The share of television viewers of evening news programs is presented in the table (NBC, CBS, ABC)
|
ABC: 6.30 |
|||
|
NSun |
NES |
||
|
ABC: 7.00 |
|||
|
N.B.WITH |
NES |
||
Find optimal company strategies for the timing of news programs
Solution Hint: There is a dominated strategy in the game
A zero-sum game in which each player has a finite set of strategies at his disposal. The rules of the matrix game are determined by the payment matrix, the elements of which are the winnings of the first player, which are also the losses of the second player.
Matrix game is an antagonistic game. The first player receives the maximum guaranteed (independent of the behavior of the second player) winnings, equal to the price of the game; similarly, the second player achieves the minimum guaranteed loss.
Under strategy is understood as a set of rules (principles) that determine the choice of action for each personal move of the player, depending on the current situation.
Now about everything in order and in detail.
Payment matrix, pure strategies, game price
IN matrix game its rules are determined payment matrix .
Consider a game in which there are two participants: the first player and the second player. Let the first player have at his disposal m pure strategies, and at the disposal of the second player - n pure strategies. Since the game is being considered, it is natural that in this game there are wins and there are losses.
IN payment matrix the elements are numbers expressing the players' wins and losses. Wins and losses can be expressed in points, amount of money or other units.
Let's create a payment matrix:
If the first player chooses i-th pure strategy, and the second player - j th pure strategy, then the payoff of the first player will be aij units, and the loss of the second player is also aij units.
Because aij + (- a ij) = 0, then the described game is a zero-sum matrix game.
The simplest example of a matrix game is coin toss. The rules of the game are as follows. The first and second players throw a coin and the result is either heads or tails. If "heads" and "heads" or "tails" or "tails" are thrown at the same time, then the first player will win one unit, and in other cases he will lose one unit (the second player will win one unit). The same two strategies are at the disposal of the second player. The corresponding payment matrix will be as follows:
The task of game theory is to determine the choice of the first player's strategy, which would guarantee him the maximum average win, as well as the choice of the second player's strategy, which would guarantee him the maximum average loss.
How do you choose a strategy in a matrix game?
Let's look at the payment matrix again:
First, let's determine the amount of winnings for the first player if he uses i th pure strategy. If the first player uses i th pure strategy, then it is logical to assume that the second player will use such a pure strategy due to which the first player’s payoff would be minimal. In turn, the first player will use such a pure strategy that would provide him with the maximum win. Based on these conditions, the winnings of the first player, which we denote as v1 , called maximin winnings or lower price of the game .
At for these values, the first player should proceed as follows. From each line, write down the value of the minimum element and select the maximum one from them. Thus, the winnings of the first player will be the maximum of the minimum. Hence the name - maximin winning. The line number of this element will be the number of the pure strategy that the first player chooses.
Now let’s determine the amount of loss for the second player if he uses j th strategy. In this case, the first player uses his own pure strategy in which the loss of the second player would be maximum. The second player must choose a pure strategy in which his loss would be minimal. The loss of the second player, which we denote as v2 , called minimax loss or top price of the game .
At solving problems on the cost of the game and determining the strategy To determine these values for the second player, proceed as follows. From each column, write down the value of the maximum element and select the minimum from them. Thus, the loss of the second player will be the minimum of the maximum. Hence the name - minimax win. The column number of this element will be the number of the pure strategy that the second player chooses. If the second player uses "minimax", then regardless of the choice of strategy by the first player, he will lose no more than v2 units.
Example 1.
 .
.

The largest of the smallest elements of the rows is 2, this is the lower price of the game, the first row corresponds to it, therefore, the maximin strategy of the first player is the first. The smallest of the largest elements of the columns is 5, this is the upper price of the game, the second column corresponds to it, therefore, the minimax strategy of the second player is the second.
Now that we have learned to find the lower and upper price of the game, the maximin and minimax strategies, it’s time to learn how to formally define these concepts.
So, the guaranteed win for the first player is:
The first player must choose a pure strategy that would provide him with the maximum of the minimum winnings. This gain (maximin) is denoted as follows:
![]() .
.
The first player uses his pure strategy so that the loss of the second player is maximum. This loss is indicated as follows:
The second player must choose his pure strategy so that his loss is minimal. This loss (minimax) is indicated as follows:
![]() .
.
Another example from the same series.
Example 2. Given a matrix game with a payoff matrix
 .
.
Determine the maximin strategy of the first player, the minimax strategy of the second player, the lower and upper price of the game.
Solution. To the right of the payment matrix, we will write out the smallest elements in its rows and note the maximum of them, and below the matrix - the largest elements in the columns and select the minimum of them:

The largest of the smallest elements of the lines is 3, this is the lower price of the game, the second line corresponds to it, therefore, the maximin strategy of the first player is the second. The smallest of the largest elements of the columns is 5, this is the upper price of the game, the first column corresponds to it, therefore, the minimax strategy of the second player is the first.
Saddle point in matrix games
If the upper and lower prices of the game are the same, then the matrix game is considered to have a saddle point. The converse is also true: if a matrix game has a saddle point, then the upper and lower prices of the matrix game are the same. The corresponding element is both the smallest in the row and the largest in the column and is equal to the price of the game.
Thus, if , then is the optimal pure strategy of the first player, and is the optimal pure strategy of the second player. That is, equal lower and upper game prices are achieved using the same pair of strategies.
In this case matrix game has a solution in pure strategies .
Example 3. Given a matrix game with a payoff matrix
 .
.
Solution. To the right of the payment matrix, we will write out the smallest elements in its rows and note the maximum of them, and below the matrix - the largest elements in the columns and select the minimum of them:
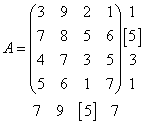
The lower price of the game coincides with the upper price of the game. Thus, the price of the game is 5. That is . The price of the game is equal to the value of the saddle point. The first player's maxin strategy is the second pure strategy, and the second player's minimax strategy is the third pure strategy. This matrix game has a solution in pure strategies.
Solve a matrix game problem yourself, and then look at the solution
Example 4. Given a matrix game with a payoff matrix
 .
.
Find the lower and upper price of the game. Does this matrix game have a saddle point?
Matrix games with optimal mixed strategy
In most cases, a matrix game does not have a saddle point, so the corresponding matrix game has no solutions in pure strategies.
But it has a solution in optimal mixed strategies. To find them, you need to assume that the game is repeated a sufficient number of times so that, based on experience, you can guess which strategy is more preferable. Therefore, the decision is associated with the concept of probability and average (mathematical expectation). In the final solution there is both an analogue of the saddle point (that is, the equality of the lower and upper prices of the game), and an analogue of the strategies corresponding to them.
So, in order for the first player to get the maximum average win and for the second player to have a minimum average loss, pure strategies should be used with a certain probability.
If the first player uses pure strategies with probabilities ![]() , then the vector
, then the vector ![]() is called a mixed first player strategy. In other words, it is a “mixture” of pure strategies. In this case, the sum of these probabilities is equal to one:
is called a mixed first player strategy. In other words, it is a “mixture” of pure strategies. In this case, the sum of these probabilities is equal to one:
![]() .
.
If the second player uses pure strategies with probabilities ![]() , then the vector
, then the vector ![]() is called a second player mixed strategy. In this case, the sum of these probabilities is equal to one:
is called a second player mixed strategy. In this case, the sum of these probabilities is equal to one:
![]() .
.
If the first player uses a mixed strategy p, and the second player - a mixed strategy q, then it makes sense expected value the first player's win (the second player's loss). To find it, you need to multiply the first player's mixed strategy vector (which will be a one-row matrix), the payoff matrix and the second player's mixed strategy vector (which will be a one-column matrix):
![]() .
.
Example 5. Given a matrix game with a payoff matrix
![]() .
.
Determine the mathematical expectation of the first player's win (the second player's loss), if the first player's mixed strategy is , and the second player's mixed strategy is .
Solution. According to the formula for the mathematical expectation of the first player’s win (the second player’s loss), it is equal to the product of the first player’s mixed strategy vector, the payment matrix and the second player’s mixed strategy vector:

The first player is called such a mixed strategy that would provide him with the maximum average payoff if the game is repeated a sufficient number of times.
Optimal mixed strategy the second player is called such a mixed strategy that would provide him with a minimum average loss if the game is repeated a sufficient number of times.
By analogy with the notation of maximin and minimax in the case of pure strategies, optimal mixed strategies are denoted as follows (and are linked to the mathematical expectation, that is, the average, of the first player’s win and the second player’s loss):
![]() ,
,
![]() .
.
In this case, for the function E there is a saddle point , which means equality.
In order to find optimal mixed strategies and a saddle point, that is, solve a matrix game in mixed strategies , you need to reduce the matrix game to a linear programming problem, that is, to an optimization problem, and solve the corresponding linear programming problem.
Reducing a matrix game to a linear programming problem
In order to solve a matrix game in mixed strategies, you need to create a straight line linear programming problem And dual task. In the dual problem, the extended matrix, which stores the coefficients of the variables in the system of constraints, free terms and coefficients of the variables in the objective function, is transposed. In this case, the minimum of the goal function of the original problem is matched to the maximum in the dual problem.
Goal function in a direct linear programming problem:
![]() .
.
System of constraints in a direct linear programming problem:
![]()
The goal function in the dual problem is:
![]() .
.
System of restrictions in the dual problem:
![]()
The optimal plan for a direct linear programming problem is denoted by
![]() ,
,
and the optimal plan for the dual problem is denoted by
We denote the linear forms for the corresponding optimal plans by and ,
and they need to be found as sums of the corresponding coordinates of optimal plans.
In accordance with the definitions of the previous paragraph and the coordinates of optimal plans, the following mixed strategies of the first and second players are valid:
![]() .
.
Theoretical mathematicians have proven that game price is expressed in the following way through the linear forms of optimal plans:
![]() ,
,
that is, it is the reciprocal of the sums of coordinates of optimal plans.
We, practitioners, can only use this formula to solve matrix games in mixed strategies. Like formulas for finding optimal mixed strategies the first and second players respectively:
in which the second factors are vectors. Optimal mixed strategies are also, as we already defined in the previous paragraph, vectors. Therefore, multiplying the number (game price) by a vector (with the coordinates of optimal plans) we also obtain a vector.
Example 6. Given a matrix game with a payoff matrix
 .
.
Find the price of the game V and optimal mixed strategies and .
Solution. We create a linear programming problem corresponding to this matrix game:

We obtain a solution to the direct problem:
![]() .
.
We find the linear form of the optimal plans as the sum of the found coordinates.
Lecture 11: Game Theory and Decision Making
Subject and tasks of game theory
Classic problems of system analysis are game-based decision-making problems under conditions of risk and uncertainty.
Both the goals of the operation, the conditions for carrying out the operation, and the conscious actions of opponents or other persons on whom the success of the operation depends can be uncertain.
Special mathematical methods, designed to justify decisions under conditions of risk and uncertainty. In some of the simplest cases, these methods make it possible to actually find and select the optimal solution. In more complex cases, these methods provide auxiliary material that allows you to better understand the complex situation and evaluate each of the possible solutions from different points of view, and make decisions taking into account its possible consequences. One of the important conditions for decision-making in this case is risk minimization.
When solving a number of practical problems in operations research (in the field of ecology, ensuring life safety, etc.), it is necessary to analyze situations in which two (or more) warring parties collide, pursuing different goals, and the result of any action of each party depends on , what course of action the enemy will choose. We can classify such situations as conflict situations.
Game theory is mathematical theory conflict situations, with the help of which it is possible to develop recommendations on the rational course of action of the parties to the conflict. To make mathematical analysis of the situation possible without taking into account secondary factors, a simplified, schematized model of the situation is built, which is called game. the game is played according to well-defined rules, which is understood as a system of conditions regulating the possible options for the players’ actions; the amount of information each party has about the other's behavior; the result of the game that each given set of moves leads to.
The result of the game (win or loss) does not always have a quantitative expression, but it is usually possible, at least conditionally, to express it with a numerical value.
A move is the choice of one of the actions provided for by the rules of the game and its implementation. Moves are divided into personal and random. A personal move is a player’s conscious choice of one of the possible options of action and its implementation. A random move is a choice from a number of possibilities, carried out not by the player’s decision, but by some random selection mechanism (tossing a coin, choosing a card from a shuffled deck, etc.). For each random move, the rules of the game determine the probability distribution of possible outcomes. The game can consist of only their personal moves, or only random moves, or a combination of both. The next main concept of game theory is the concept of strategy. A strategy is a system of decisions a priori adopted by the player (of the “if-then” type), which he adheres to while playing the game, which can be presented in the form of an algorithm and executed automatically.
The goal of game theory is to develop recommendations for the reasonable behavior of players in a conflict situation, i.e., to determine the “optimal strategy” for each of them. A strategy that is optimal for one indicator will not necessarily be optimal for others. Being aware of these limitations and therefore not blindly adhering to the recommendations obtained by game methods, one can still wisely use the mathematical apparatus of game theory to develop, if not exactly optimal, then at least an “acceptable” strategy.
Games can be classified: by the number of players, the number of strategies, the nature of interaction between players, the nature of winning, the number of moves, the state of information, etc. .
Depending on the number of players There are games of two and n players. The first of them are the most studied. Games of three or more players have been less studied due to the fundamental difficulties encountered and the technical possibilities of obtaining a solution.
Depending on the number of possible strategies, games are divided into “ final" And " endless».
A game is called finite if each player has only a finite number of strategies, and infinite if at least one of the players has an infinite number of strategies.
By the nature of interaction games are divided into non-coalition games: players do not have the right to enter into agreements or form coalitions; coalition (cooperative) - can join coalitions.
In cooperative games, coalitions are predetermined.
By nature of winnings games are divided into: zero-sum games (the total capital of all players does not change, but is redistributed between players; the sum of winnings of all players is zero) and non-zero-sum games.
By type of payoff functions games are divided into: matrix, bimatrix, continuous, convex, etc.
Matrix the game is a finite game of two players with a zero sum, in which the payoff of player 1 is given in the form of a matrix (the row of the matrix corresponds to the number of the applied strategy of player 1, the column - the number of the applied strategy of the player; at the intersection of the row and column of the matrix is the payoff of player 1, corresponding to the applied strategies ).
For matrix games, it has been proven that any of them has a solution and it can be easily found by reducing the game to a linear programming problem.
Bimatrix the game is a finite game of two players with a non-zero sum, in which the payoffs of each player are specified by matrices separately for the corresponding player (in each matrix, the row corresponds to the strategy of player 1, the column to the strategy of player 2, at the intersection of the row and column in the first matrix is the payoff of player 1 , in the second matrix - the player’s winnings)
Continuous A game is considered to be one in which the payoff function of each player is continuous. It has been proven that games of this class have solutions, but no practically acceptable methods for finding them have been developed.
If the payoff function is convex, then such a game is called convex. Acceptable solution methods have been developed for them, consisting of finding the pure optimal strategy (a certain number) for one player and the probabilities of using the pure optimal strategies of the other player. This problem is solved relatively easily.
Writing a matrix game as a payoff matrix
Consider a finite game in which the first player A has m strategies, and the second player B-n strategies. This game is called the m×n game. Let us denote the strategies A 1 , A 2 , ..., A m ; and B 1, B 2, ..., B n. Let's assume that each side has chosen a certain strategy: A i or B j. If the game consists only of personal moves, then the choice of strategies uniquely determines the outcome of the game - the win of one of the parties a ij . If the game contains, in addition to personal, random moves, then the payoff for a pair of strategies A i and B is a random variable depending on the outcomes of all random moves. In this case, a natural estimate of the expected gain is the mathematical expectation of a random gain, which is also denoted by a ij.
Let us assume that we know the values of a ij for each pair of strategies. These values can be written in the form of a rectangular table (matrix), the rows of which correspond to strategies A i , and the columns to strategies B j .
Then, in general, the matrix game can be written as the following payoff matrix:
| B 1 | B 2 | ... | Bn | |
|---|---|---|---|---|
| A 1 | a 11 | a 12 | ... | a 1n |
| A 2 | a 21 | a 22 | ... | a 2n |
| ... | ... | ... | ... | ... |
| Am | a m1 | a m2 | ... | a mn |
Table - General form payoff matrix matrix game
where A i are the names of the strategies of player 1, B j are the names of the strategies of player 2, a ij are the payoff values of player 1 when he chooses the i-th strategy, and player 2 - j-th strategy. Since this game is a zero-sum game, the payoff value for player 2 is the opposite sign of the payoff value for player 1.
The concept of the lower and upper price of the game. Solution of the game in pure strategies
Each player strives to maximize his winnings, taking into account the behavior of the opposing player. Therefore, for player 1 it is necessary to determine the minimum payoff values in each of the strategies, and then find the maximum of these values, that is, determine the value
V n = max i min j a ij
or find the minimum values for each row of the payment matrix, and then determine the maximum of these values. The value V n is called maximin matrices or lower price of the game. The player's strategy that corresponds to the maximin V n is called the maximin strategy.
Obviously, if we adhere to the maximin strategy, then regardless of the enemy’s behavior, we are guaranteed a win no less than V n. Therefore, the value of Vn is the guaranteed minimum that we can provide ourselves by adhering to our most cautious strategy.
The value of player 1’s gain is equal, by definition of a matrix game, to the amount of player’s loss. Therefore, for player 2 it is necessary to determine the value
V in = min j max i a ij
Or find the maximum values for each of the columns of the payment matrix, and then determine the minimum of these values. The value V in is called minimax matrices, top price of the game or minimax winnings. The opponent's winning strategy is called his minimax strategy. By adhering to his most cautious minimax strategy, the opponent is guaranteed that in any case he will lose no more than V century.
If the values of V n and V in do not coincide, while maintaining the rules of the game (coefficients a ij) in the long term, the choice of strategies by each player turns out to be unstable. It acquires stability only when V n = V c = V. In this case, they say that the game has solution in pure strategies, and strategies in which V is achieved are optimal pure strategies. The quantity V is called at the pure price of the game .
For example, in a matrix:
| B 1 | B 2 | B 3 | B 4 | Min j | |
|---|---|---|---|---|---|
| A 1 | 17 | 16 | 15 | 14 | 14 |
| A 2 | 11 | 18 | 12 | 13 | 11 |
| A 3 | 18 | 11 | 13 | 12 | 11 |
| Max i | 18 | 18 | 15 | 14 |
Table - Payment matrix in which there is a solution in pure strategies
There is a solution in pure strategies. In this case, for player 1 the optimal pure strategy will be strategy A 1 , and for player 2 - strategy B 4 .
In the matrix, there is no solution in pure strategies, since the lower price of the game is achieved in strategy A 1 and its value is 12, while the upper price of the game is achieved in strategy B 4 and its value is 13.
| B 1 | B 2 | B 3 | B 4 | Min j | |
|---|---|---|---|---|---|
| A 1 | 17 | 16 | 15 | 12 | 12 |
| A 2 | 11 | 18 | 12 | 13 | 11 |
| A 3 | 18 | 11 | 13 | 12 | 11 |
| Max i | 18 | 18 | 15 | 13 |
Table - Payment matrix in which there is no solution in pure strategies
Reducing the order of the payoff matrix
The order of the payoff matrix (number of rows and columns) can be reduced by eliminating dominated and duplicate strategies.
Strategy K* is called dominated strategy K**, if for any variant of behavior of the opposing player the relation is satisfied
A k*< A k** ,
where A k* and A k** are the payoff values when the player chooses strategies K* and K**, respectively.
If the relation is satisfied
strategy K* is called duplicate with respect to strategy K**.
For example, in a matrix with dominated and duplicate strategies, strategy A 1 is dominated by strategy A 2, strategy B 6 is dominated by strategies B 3, B 4 and B 5, and strategy B 5 is duplicated by strategy B 4 .
| B 1 | B 2 | B 3 | B 4 | B 5 | B 6 | |
|---|---|---|---|---|---|---|
| A 1 | 1 | 2 | 3 | 4 | 4 | 7 |
| A 2 | 7 | 6 | 5 | 4 | 4 | 8 |
| A 3 | 1 | 8 | 2 | 3 | 3 | 6 |
| A 4 | 8 | 1 | 3 | 2 | 2 | 5 |
Table - Payment Matrix with Dominated and Duplicate Strategies
These strategies will not be chosen by players, since they are obviously losing and removing these strategies from the payment matrix will not affect the determination of the lower and upper prices of the game described by this matrix.
The set of non-dominated strategies obtained after reducing the dimension of the payment matrix is also called the Pareto set.
Examples of games
1. Game "Chicken"
The game of Chicken involves players engaging in interactions that result in each player being seriously harmed until one player quits the game. Example use of this game - interaction motor vehicle, for example, situations where two cars are heading towards each other and the one that swerves first is considered the "wimp" or "chicken". The point of the game is to create tension that would lead to the elimination of the player. This situation is often found among teenagers or aggressive young people, although sometimes it carries less risk. Another application of this game is a situation in which two political parties come into contact in which they have nothing to gain, and only pride forces them to maintain opposition. Parties hesitate to make concessions until they reach the final point. The resulting psychological tension can lead one of the players to the wrong behavior strategy: if none of the players gives in, then a collision and a fatal outcome are inevitable.
The payment matrix of the game looks like this:
| Give in | Don't give in | |
|---|---|---|
| Give in | 0, 0 | -1, +1 |
| Don't give in | +1, -1 | -100, -100 |
2. Game “kite and dove”
The game "kite and pigeon" is a biological example of a game. In this version, two players with unlimited resources choose one of two strategies. The first ("dove") involves the player demonstrating his strength by intimidating the opponent, and the second ("kite") involves the player physically attacking the opponent. If both players choose the "kite" strategy, they fight, injuring each other. If one of the players chooses the “kite” strategy, and the second “dove”, then the first defeats the second. If both players are “pigeons,” then the opponents come to a compromise, receiving a payoff that turns out to be less than the payoff of the “kite” defeating the “dove,” as follows from the payoff matrix of this game.
Here V is the price of agreement, C is the price of conflict, and V In the kite and dove game there are three Nash equilibrium points: The Prisoner's Dilemma is one of the most common conflict situations considered in game theory. The classic prisoner's dilemma goes like this: two suspects, A and B, are in different cells. The investigator, visiting them individually, offers the following deal: if one of them testifies against the other, and the second remains silent, then the first prisoner will be released, and the second will be sentenced to 10 years. If both remain silent, they will serve 6 months. If both betray each other, then each will receive 2 years. Each of the prisoners must make a decision: to betray his accomplice or remain silent, not knowing what decision the other made. Dilemma: what decision will the prisoners make? Game payment matrix: In this case, the result is based on the decision of each of the prisoners. The situation of the players is complicated by the fact that they do not know what decision the other has made, and by the fact that they do not trust each other. The best strategy for the players will be cooperation, in which both remain silent and receive the maximum payoff (shorter period), each other solution will be less win-win. Let us analyze the “prisoner’s dilemma”, moving for clarity to the payment matrix of the canonical form: According to this matrix, the cost of mutual refusal to cooperate (S) is 1 point for each player, the cost of cooperation (R) is 3 points, and the cost of temptation to betray the other (T) is 5 points. We can write the following inequality: T > R > S. When repeating the game several times, the choice of cooperation outweighs the temptation to betray and get the maximum win: 2 R > T + S. A Nash equilibrium is a situation where no player has an incentive to change its strategy given the strategy of another player (another firm), allowing the players to reach a compromise solution. The definition of Nash equilibrium and its existence is defined as follows. Let (S, f) be a game in which S is the set of strategies and f is the set of payoffs. When each player i ∈ (1, ..., n) chooses strategy x i &isin S, where x = (x 1 , ..., x n), then player i receives payoff f i (x). Winning depends on the strategy chosen by all players. A strategy x* ∈ S is a Nash equilibrium if no deviation from it by any one player brings him a profit, that is, for all i the following inequality holds: f i (x*) ≥ f i (x i , x* -i) For example, the Prisoner's Dilemma game has one Nash equilibrium—a situation in which both prisoners betray each other. The easiest way to determine the Nash equilibrium is by using the payoff matrix, especially in cases where the game involves two players who have more than two strategies in their arsenal. Since in this case the formal analysis will be quite complex, a mnemonic rule is applied, which is as follows: a cell of the payoff matrix represents a Nash equilibrium if the first number in it is the maximum among all values presented in the columns, and the second number , standing in the cell is the maximum number among all lines. For example, apply this rule to a 3x3 matrix: Nash equilibrium points: (B,A), (A,B) and (C,C). Indeed, for cell (B,A), since 40 is the maximum value in the first column, 25 is the maximum value in the second row. For cell (A,B), 25 is the maximum value in the second column, 40 is the maximum value in the second row. The same goes for cell (C,C). Let's look at an example of the pollution game ( environment). Here the object of our attention will be this view side effects production as pollution. If firms never asked anyone what to do, any of them would rather create pollution than install expensive purifiers. If any company decided to reduce harmful emissions, then costs, and, consequently, prices for its products, would increase, and demand would fall. It is quite possible that this company would simply go bankrupt. Living in the cruel world of natural selection, firms would rather remain in Nash equilibrium (cell D), in which there is no need to spend money on treatment facilities and technologies. No firm will be able to increase profits by reducing pollution. Table - Payment matrix of the environmental pollution game. Once in the economic game, every unregulated, profit-maximizing steel firm will produce water and air pollution. If any firm tries to clean up its emissions, it will be forced to raise prices and suffer losses. Non-cooperative behavior will establish a Nash equilibrium under high emissions conditions. The government can take measures to ensure that the equilibrium moves to cell A. In this situation, pollution will be negligible, but profits will remain the same. Pollution games are one of the cases where the mechanism of the “invisible hand” does not work. This is a situation where the Nash equilibrium is inefficient. Sometimes such uncontrolled games become dangerous and the government may intervene. By establishing a system of emissions fines and quotas, the government can induce firms to choose outcome A, which corresponds to low pollution levels. Firms earn exactly the same as before, with large emissions, and the world becomes somewhat cleaner. Let's consider an example of solving a matrix game in pure strategies, in a real economy, in a situation where two enterprises are fighting for the market for a region's products. Two enterprises produce products and supply them to the regional market. They are the only suppliers of products to the region, therefore they completely determine the market for these products in the region. Each of the enterprises has the ability to produce products using one of three different technologies. Depending on the environmental friendliness of the technological process and the quality of the products produced by each technology, enterprises can set the unit price at 10, 6 and 2 monetary units, respectively. At the same time, enterprises have different costs per unit of production. Table - Costs per unit of products produced at enterprises in the region (units). As a result of marketing research of the regional product market, the demand function for products was determined: Y = 6 - 0.5⋅X, where Y is the quantity of products that the population of the region will purchase (thousand units), and X is the average price of enterprises’ products, unit units. Data on demand for products depending on sales prices are given in the table: Sales price 1 unit. products, e.g. Average selling price of 1 unit. products, e.g. Demand for products, thousand units Table - Demand for products in the region, thousand units. The values of the Share of products of enterprise 1 purchased by the population depend on the ratio of prices for the products of enterprise 1 and the enterprise. As a result of marketing research, this dependence was established and the values were calculated: Table - Share of enterprise 1 products purchased by the population depending on the ratio of product prices According to the problem, there are only 2 enterprises operating in the regional market. Therefore, the share of the second enterprise’s products purchased by the population, depending on the ratio of product prices, can be defined as one minus the share of the first enterprise. The strategies of enterprises in this problem are their decisions regarding production technologies. These decisions determine the cost and selling price per unit of production. In the task it is necessary to determine: The profit of the enterprise in this problem depends on: Thus, the values of the difference in the profit of enterprises corresponding to the coefficients of the payment matrix must be determined using the formula: D = p⋅(S⋅R1 - S⋅C1) - (1 - p)⋅(S⋅R2 - S⋅C2), where D is the difference in profit from the production of enterprise 1 and enterprise products p is the share of enterprise 1’s products purchased by the population of the region; S is the amount of products purchased by the population of the region; R1 and R2 - sales prices per unit of production by enterprises 1 and C1 and C2 - the total cost of a unit of production produced at enterprises 1 and Let's calculate one of the coefficients of the payment matrix. Let, for example, enterprise 1 decide to produce products in accordance with technology III, and enterprise 2 - in accordance with technology II. Then the selling price per unit. products for enterprise 1 will amount to 2 units. at unit cost. products 1.5 units For enterprise 2, the selling price per unit. products will amount to 6 units. at a cost of 4.00. The amount of products that the population of the region will purchase when average price 4 units equals 4 thousand units. (Table 1). The share of products that the population will purchase from enterprise 1 will be 0.85, and from enterprise 2 - 0.15 (Table 1.3). Let's calculate the coefficient of the payment matrix a 32 using the formula: a 32 = 0.85⋅(4⋅2 - 4×1.5) - 0.15⋅(4⋅6 - 4⋅4) = 0.5 thousand units. where i=3 is the technology number of the first enterprise, and j=2 is the technology number of the second enterprise. Similarly, we calculate all the coefficients of the payment matrix. In the payment matrix, strategies A 1 - A 3 - represent decisions about production technologies for enterprise 1, strategies B 1 - B 3 - decisions about production technologies for enterprise 2, winning coefficients - the difference between the profits of enterprise 1 and enterprise Table - Payment matrix in the game “Struggle between two enterprises”. There are no dominant or overlapping strategies in this matrix. This means that for both enterprises there are no obviously unprofitable production technologies. Let us determine the minimum elements of the matrix rows. For enterprise 1, each of these elements has the value of the minimum guaranteed gain when choosing the appropriate strategy. The minimum elements of the matrix by row have the following values: 0.17, -1.5, 0.4. Let us determine the maximum elements of the matrix columns. For enterprise 2, each of these elements also has the value of the minimum guaranteed gain when choosing the appropriate strategy. The maximum matrix elements by column have the following values: 3, 0.62, 0.4. The lower price of the game in the matrix is 0.4. The top price of the game is also 0.4. Thus, the lower and upper price of the game in the matrix are the same. This means that there is a technology for producing products that is optimal for both enterprises under the conditions of a given task. This is technology III, which corresponds to strategies A 3 of enterprise 1 and B 3 of enterprise Strategies A 3 and B 3 are pure optimal strategies in this problem. The difference between the profits of enterprise 1 and enterprise 2 when choosing a pure optimal strategy is positive. This means that enterprise 1 will win this game. The profit of enterprise 1 will be 0.4 thousand. At the same time, 5 thousand units will be sold on the market. products (sales equal to demand for products, table 1). Both enterprises will set the price per unit of production at 2.00. In this case, for the first enterprise the total cost per unit of production will be 1.5 units, and for the second - 1 unit. Enterprise 1 will benefit only due to the high share of products that the population will purchase from it. The decision maker determines the most profitable strategy depending on the target setting that he implements in the process of solving the problem. The decision maker determines the result of solving the problem according to one of decision criteria. In order to come to an unambiguous and, if possible, most profitable solution, it is necessary to introduce an evaluation (target) function. In this case, each decision maker strategy (A i) is assigned a certain result Wi, which characterizes all the consequences of this decision. From the array of decision-making results, the decision maker selects the element W that best reflects the motivation of his behavior. Depending on conditions external environment and the degree of informativeness of the decision-maker, the following classification of decision-making tasks is made: The use of the expected value criterion is driven by the desire to maximize expected profits (or minimize expected costs). The use of expected values implies the possibility of repeatedly solving the same problem until sufficiently accurate calculation formulas are obtained. Mathematically it looks like this: let X - random value with mathematical expectation MX and variance DX. If x 1 , x 2 , ..., x n are the values of the random variable (r.v.) X, then the arithmetic mean of their (sample mean) values x^=(x 1 +x 2 +...+x n)/ n has a variance of DX/n. Thus, when n→∞ DX/n→∞ and X→MX. In other words, with a sufficiently large sample size, the difference between the arithmetic mean and the mathematical expectation tends to zero (the so-called limit theorem of probability theory). Consequently, the use of the expected value criterion is valid only in the case when the same solution has to be applied a sufficiently large number of times. The opposite is also true: focusing on expectations will lead to incorrect results for decisions that have to be made a small number of times. Example 1. It is necessary to make a decision about when it is necessary to carry out preventive repairs of the PC in order to minimize losses due to malfunctions. If repairs are carried out too often, maintenance costs will be high with small losses due to accidental breakdowns. Since it is impossible to predict in advance when a malfunction will occur, it is necessary to find the probability that the PC will fail in time period t. This is the element of “risk”. Mathematically, it looks like this: the PC is repaired individually if it stops due to a breakdown. At T time intervals, preventative repairs are performed on all n PCs. It is necessary to determine the optimal value of m, at which the total costs of repairing faulty PCs and carrying out preventive repairs per one time interval are minimized. Let p t be the probability of one PC failing at time t, and n t be a random variable equal to the number of all PCs failing at the same moment. Let us further assume that C 1 is the cost of repairing a faulty PC and C 2 is the cost of preventive repair of one machine. The use of the expected value criterion in this case is justified if PCs operate for a long period of time. In this case, the expected costs for one interval will be OZ = (C 1 ∑M(n t)+C 1 n)/T, where M(n t) is the mathematical expectation of the number of failed PCs at time t. Since n t has binomial distribution with parameters (n, p t), then M(n t) = np t. Thus OZ = n(C 1 ∑p t +C 2)/T. The necessary conditions for optimality T * have the form: OZ (T * -1) ≥ OZ (T *), HP (T * +1) ≥ HP (T *). Therefore, starting from a small value of T, calculate the OP( T) until satisfied the necessary conditions optimality. Let C 1 = 100; C 2 = 10; n = 50. Values p t have the form: T * →3, OZ(T *)→366.7 Therefore, preventive maintenance must be done at T * = 3 time intervals. The expected value criterion can be modified so that it can be applied to situations that rarely occur. If x - c. V. with dispersion DX, then the arithmetic mean x^ has dispersion DX/n, where n is the number of terms in x^. Therefore, if DX decreases, the probability that x^ is close to MX increases. Therefore, it is advisable to introduce a criterion in which maximizing the expected value of profit is combined with minimizing its dispersion. Example 2. Let us apply the “expected value - variance” criterion for example 1. To do this, it is necessary to find the variance of costs over one time interval, i.e. dispersion з Т =(C 1 ∑n t +C 2 n)/T Because n t , t = (1, T-1) is a r.v., then s T is also a r.v. S.v. n t has a binomial distribution with M(n t) = np t and D(n t) = np t (1–p t). Hence, D(з Т) = D((C 1 ∑n t +C 2 n)/T) = (C 1 /T) 2 D(∑n t) = = (C 1 /T) 2 ∑Dn t = (C 1 /T) 2 ∑np t (1-p t) = (C 1 /T) 2 (∑p t - ∑p t 2 ), where C 2 n = const. From example 1 it follows that M(z T) = M(z(T)). Therefore, the required criterion will be the minimum of the expression M(z(T)) + to D(z T). Comment. The constant "k" can be considered as a level risk averse, because “k” determines the “degree of possibility” of dispersion D(z T) in relation to mathematical expectation. For example, if an entrepreneur reacts particularly sharply to large negative deviations of profit down from M(z(T)), then he can choose “k” much greater than 1. This gives more weight to the variance and leads to a decision that reduces the likelihood of large losses in profit. For k=1 we get the problem M(z(T))+D(z(T)) = n ( (C 1 /T+C 1 2 /T 2)∑p t - C 1 2 /T 2 ∑p t 2 + C 2 /T ) Using the data from example 1, you can create the following table The table shows that preventive maintenance must be done during each interval T * =1. The ceiling criterion does not provide an optimal solution that maximizes, for example, profit or minimizes costs. Rather, it corresponds to the definition acceptable way of action. Example 3. Let us assume that the quantity of demand x per unit of time (demand intensity) for some product is given by a continuous distribution function f(x). If inventories are small at the beginning, there may be a shortage of goods in the future. Otherwise, by the end of the period under review, inventories of unsold goods may turn out to be very large. In both cases, losses are possible. Because It is very difficult to determine losses from shortages; the decision maker can set the required level of inventories in such a way that the value expected deficit did not exceed A 1 units, and the value expected the surplus did not exceed A 2 units. In other words, let I be the desired inventory level. Then expected deficit = ∫(x-I)f(x)dx ≤ A 1 , expected surplus = ∫(I-x)f(x)dx ≤ A 2 . If A 1 and A 2 are chosen arbitrarily, these conditions may turn out to be contradictory. In this case, one of the restrictions must be relaxed to ensure admissibility. Let, for example, f(x) = 20/x 2, 10≤x≤20, f(x) = 0, x≤10 and x≥20. ∫(x-I)f(x)dx = ∫(x-I)(20/x 2)dx = 20(ln(20/I) + I/20 – 1) ∫(I-x)f(x)dx = ∫(I-x)(20/x 2)dx = 20(ln(10/I) + I/10 – 1) Application of the limit level criterion leads to inequalities ln(I) - I/20 ≥ ln(20) – A 1 /20 – 1 = 1.996 - A 1 /20 ln(I) - I/10 ≥ ln(10) – A 2 /20 – 1 = 1.302 - A 2 /20 The limit values A 1 and A 2 must be chosen so that both inequalities are satisfied for at least one value of I. For example, if A 1 = 2 and A 2 = 4, the inequalities take the form ln(I) - I/20 ≥ 1.896 ln(I) - I/10 ≥ 1.102 The value of I must be between 10 and 20, because It is within these limits that demand changes. The table shows that both conditions are met for I, from the interval (13,17) Any of these values satisfies the conditions of the problem. We will assume that the decision maker is not confronted reasonable enemy. The data needed to make a decision under uncertainty is usually given in the form of a matrix, the rows of which correspond to possible actions, and the columns correspond to possible states of the system. Suppose, for example, that a product needs to be made from some material, the durability of which cannot be determined at acceptable costs. The loads are assumed to be known. You need to decide what dimensions a product made from this material should have. The possible solutions are: E 1 - selection of sizes for reasons of maximum durability; E m - choice of sizes for reasons of minimum durability; E i are intermediate solutions. The conditions to be considered are: F 1 - conditions ensuring maximum durability; F n - conditions ensuring min durability; F i are intermediate conditions. The result of the decision e ij = e(E i ; F j) here can be understood as an assessment corresponding to the option E i and the conditions F j and characterizing profit, utility or reliability. Typically we will call this result usefulness of the solution. Then the family (matrix) of solutions ||e ij || has the form: To come to an unambiguous and, if possible, the most profitable solution, it is necessary to introduce an evaluation (target) function. In this case, the decision matrix ||e ij || reduced to one column. Each option E i is assigned, i.e., a certain result e ir, which characterizes, in general, all the consequences of this decision. We will further denote this result by the same symbol e ir. The rule for choosing a solution in accordance with the minimax criterion (MM criterion) can be interpreted as follows: the decision matrix is supplemented with one more column from the smallest results e ir of each row. It is necessary to select those options in the rows of which have the highest value e ir of this column. Selected t.o. options completely eliminate the risk. This means that the decision maker cannot face a worse outcome than the one he is targeting. This property allows us to consider the MM criterion one of the fundamental ones. The use of the MM criterion is justified if the situation in which the decision is made is as follows: Let us denote by q i the probability of the appearance of the external state F j . The corresponding selection rule can be interpreted as follows: the decision matrix is supplemented with another column containing the mathematical expectation of the values of each of the rows. Those options are selected whose rows contain the largest value e ir of this column. It is assumed that the situation in which the decision is made is characterized by the following circumstances: When enough large quantities implementations, the average value gradually stabilizes. Therefore, with full (infinite) implementation, any risk is practically eliminated. That. The Bayes-Laplace criterion (B-L criterion) is more optimistic than the minimax criterion, but it requires greater awareness and a fairly long implementation period. a ij:= max i (e ij) - e ij e ir:= max i (a ij) = max j (max i (e ij) - e ij) The value a ij can be interpreted as the maximum additional gain that is achieved if in state F j instead of option E i one chooses another option that is optimal for this external state. The value a ij can also be interpreted as losses (fines) arising in state F j when replacing the optimal option for it with option E i . In the latter case, e ir represents the maximum possible (over all external states F j, j = (1,n)) losses in the case of choosing option E i. The selection rule corresponding to Savage's criterion is now interpreted as follows: The requirements for the situation in which a decision is made coincide with the requirements for the MM criterion. From the requirements for the criteria considered, it becomes clear that, due to their rigid starting positions, they are applicable only for idealized practical solutions. In cases where too strong an idealization is possible, different criteria can be applied simultaneously in turn. After this, among several options, the decision maker chooses the final decision using a volitional method. This approach allows, firstly, to better penetrate into all the internal connections of the decision-making problem and, secondly, weakens the influence of the subjective factor. Example. When operating a computer, it is necessary to periodically pause information processing and check the computer for viruses. A pause in information processing leads to certain economic costs. If the virus is not detected in time, some of the information may be lost, which will lead to even greater losses. The possible solutions are: E 1 - full check; E 2 - minimum check; E 3 - refusal to check. The computer can be in the following states: F 1 - no virus; F 2 - there is a virus, but it did not have time to damage the information; F 3 - there are files that need to be restored. The results, including the costs of searching for the virus and its elimination, as well as the costs associated with information recovery, have the form: According to the MM criterion, a full check should be carried out. Bayes-Laplace criterion, under the assumption that all states of the machine are equally probable. The example is specially selected so that each criterion offers a new solution. The uncertainty of the state in which the check finds the computer turns into uncertainty about which criterion to follow. Since different criteria are associated with different conditions, in which a decision is made, the best thing for a comparative assessment of the recommendations of certain criteria is to obtain additional information about the situation itself. In particular, if the decision being made concerns hundreds of machines with the same parameters, then it is recommended to use the Bayes-Laplace criterion. If the number of machines is not large, it is better to use the minimax or Savage criteria. Trying to take the most balanced position, Hurwitz proposed an evaluative function that falls somewhere between the point of view of extreme optimism and extreme pessimism: max i (e ir) = ( C⋅min j (e ij) + (1-C)⋅max j (e ij) ), where C is the weighting factor. The selection rule according to the Hurwitz criterion is formed as follows: decision matrix ||e ij || is supplemented by a column containing the weighted average of the smallest and largest results for each row. Only those options are selected whose rows contain the largest elements e e ir of this column. At C=1, the Hurwitz criterion turns into the MM criterion. When C = 0 it turns into the “gambler” criterion max i (e ir) = max i (max j (e ij)), those. we take the point of view of a gambler who bets that the best chance will “come up.” In technical applications, it is difficult to choose the weighting factor C, because It is difficult to find a quantitative characteristic for those shares of optimism and pessimism that are present when making a decision. Therefore, most often C: = 1/2. The Hurwitz criterion is applied when: This criterion is based simultaneously on the MM criterion and the Bayes-Laplace criterion. The parameter n expresses the degree of confidence in the probability distribution used. If the confidence is high, then the Bayes-Laplace criterion dominates, otherwise the MM criterion dominates, i.e. we are looking for max i (e ir) = max i (v⋅∑e ij ⋅q i + (1-v) min j (e ir)), 0 ≤ n ≤ 1. The selection rule corresponding to the Hodge-Lehman criterion is formed as follows: decision matrix ||e ij || is supplemented by a column composed of weighted averages (with weight v≡const) mathematical expectations and the smallest result of each row (*). Those solution options in the rows of which have the largest value in this column are selected. At v = 1, the Hodge-Lehman criterion becomes the Bayes-Laplace criterion, and at v = 0 it becomes a minimax criterion. The choice of v is subjective because the degree of reliability of any distribution function is a murky matter. To apply the Hodge-Lehman criterion, it is desirable that the situation in which the decision is made satisfies the following properties: This criterion is focused on the amount of losses, i.e. to negative values of all e ij . Wherein max i (e ir) = max i (min j (e ij)q j) . Because in economic problems they primarily deal with prices and costs, conditione e ij<0 обычно выполняется. В случае же, когда среди величин e ij встречаются и положительные значения, можно перейти к строго отрицательным значениям с помощью преобразования e ij -a при подходящем образом подобранном a>0. In this case, the optimal solution depends on a. The selection rule according to the Germeyer criterion is formulated as follows: decision matrix ||e ij || is supplemented by another column containing in each row the smallest product of the result available in it and the probability of the corresponding state F j . Those options are selected in the rows of which the largest value e e ij of this column is found. In a sense, the Germeyer criterion generalizes the MM criterion: in the case of a uniform distribution q j = 1/n, j=(1,n), they become identical. The conditions for its applicability are as follows: If the distribution function is not known very reliably, and the realization numbers are small, then, following the Germeyer criterion, one obtains, generally speaking, an unreasonably large risk. The desire to obtain criteria that would be better adapted to the existing situation than all those considered so far led to the construction of the so-called composite criteria. As an example, consider a criterion obtained by combining the Bayes-Laplace and minimax criteria (BL(MM) criterion). The selection rule for this criterion is formulated as follows: decision matrix ||e ij || is supplemented by three more columns. In the first of them the mathematical expectations of each of the lines are written, in the second - the difference between the reference value e i 0 j 0 = max i (max j (e ij)) and the smallest value the corresponding line. The third column contains the differences between the largest value each row and the largest value max j (e i 0 j) of the row in which the value e i 0 j 0 is located. Those options are selected whose rows (subject to the relationships given below between the elements of the second and third columns) give the greatest mathematical expectation. Namely, the corresponding value e i 0 j 0 - max j (e ij) from the second column must be or equal to some predetermined risk level E add. The value from the third column must be greater than the value from the second column. The application of this criterion is due to the following characteristics of the situation in which the decision is made: The BL(MM) criterion is well suited for constructing practical solutions, primarily in the field of technology, and can be considered quite reliable. However, the given limits of risk E additional and, accordingly, risk assessments E i do not take into account either the number of applications of the solution or other similar information. The influence of the subjective factor, although weakened, is not completely excluded. max j (e ij)-max j (e i 0 j)≥E i is essential in cases where the solution is implemented only once or a small number of times. In these conditions, it is not enough to focus on the risk associated only with unfavorable external conditions and average values. Because of this, however, you can suffer some losses in successful external states. With a large number of implementations, this condition ceases to be so important. It even allows for reasonable alternatives. However, there are no clear quantitative indications in which cases this condition should be omitted. max i (e ir):= max i (∏e ij) The selection rule in this case is formulated as follows: Decision matrix ||e ij || is supplemented by a new column containing the products of all the results of each row. Those options are selected whose lines contain highest values this column. The application of this criterion is due to the following circumstances: The product criterion is adapted primarily for cases where all e ij are positive. If the positivity condition is violated, then some shift e ij +a should be performed with some constant a>|min ij (e ij)|. The result will naturally depend on a. In practice most often a:= |min ij (e ij)|+1. If no constant can be recognized as having meaning, then the product criterion is not applicable. Let's look at the same example as before (see above). The construction of an optimal solution for the matrix of decisions on checks according to the Hurwitz criterion has the form (at C = 0, in 10 3): In this example, the solution has a turning point with respect to the weighting factor C: up to C = 0.57, E 3 is selected as optimal, and for larger values, E 1 is chosen. Application of the Hodge-Lehman criterion (q=0.33, v=0, in 10 3): The Hodge-Lehman criterion recommends option E 1 (full verification) - just like the MM criterion. The recommended option changes only at v=0.94. Therefore, a uniform distribution of states of the machine in question must be recognized with a very high probability so that it can be selected based on its higher mathematical expectation. In this case, the number of implementations of the solution always remains arbitrary. The Germeyer criterion at q j = 0.33 gives the following result (in 10 3): Option E 1 is selected as the optimal one. Comparison of options using the value e ir shows that the way the Germeier criterion operates is even more flexible than that of the MM criterion. In the table below, the solution is selected in accordance with the BL(MM) criterion at q 1 =q 2 =q 3 =1/2 (data in 10 3). Option E 3 (refusal of verification) is accepted by this criterion only when the risk approaches Epossible = 15⋅10 3 . Otherwise, E 1 turns out to be optimal. In many technical and business problems, the acceptable risk is much lower, usually amounting to only a small percentage of the total costs. In such cases, it is especially valuable if the inaccurate value of the probability distribution does not have a very strong impact. If it turns out to be impossible to establish the acceptable risk E additional in advance, regardless of the decision made, then calculating the expected risk E possible can help. Then it becomes possible to consider whether such a risk is justified. Such research is usually easier. The results of applying the product criterion for a = 41⋅10 3 and a = 200⋅10 3 have the form: The condition e ij > 0 is not satisfied for this matrix. Therefore, first a = 41⋅10 3 and then a = 200⋅10 3 are added to the elements of the matrix (by external arbitrariness). For a = 41⋅10 3 option E 1 turns out to be optimal, and for a = 200⋅10 3 option E 3 turns out to be optimal, so the dependence of the optimal option on a is obvious.3. Prisoner's dilemma
—
Cooperation
Refusal to cooperate
Cooperation
3, 3
0, 5
Refusal to cooperate
5, 0
1, 1
Nash equilibrium.
A
B
C
A
0, 0
25, 40
5, 10
B
40, 25
0, 0
5, 15
C
10, 5
15, 5
10, 10
Firm 1
Firm 2
Low pollution
High level of pollution
Low pollution
A
100,100
IN
-30,120
High level of pollution
WITH
120,-30
D
100,100
An example of solving a matrix game in pure strategies
Task.
Enterprise 1
Enterprise 2
10
10
10
1
10
6
8
2
10
2
6
3
6
10
8
2
6
6
6
3
6
2
4
4
2
10
6
3
2
6
4
4
2
2
2
5
The solution of the problem
B 1
B 2
B 3
Min j
A 1
0,17
0,62
0,24
0,17
A 2
0,3
-1,5
-0,8
-1
A 3
0,9
0,5
0,4
0,4
Max i
3
0,62
0,4
Decision Criteria
Decision making under risk conditions.
1. Expected value criterion.
T
p t
∑р t
OZ(T)
1
0.05
0
50(100⋅0+10)/1=500
2
0.07
0.05
375
3
0.10
0.12
366.7
4
0.13
02
400
5
0.18
0.35
450
“Expected value - variance” criterion.
T
p t
p t 2
∑p t
∑p t 2
M(z(T))+D(z(T))
1
0,05
0,0025
0
0
500.00
2
0,07
0,0049
0,05
0,0025
6312,50
3
0,10
0,0100
0,12
0,0074
6622,22
4
0,13
0,0169
0,2
0,0174
6731,25
5
0,18
0,0324
0,35
0,0343
6764,00
3. Limit level criterion
I
10
11
12
13
14
15
16
17
18
19
20
ln(I) - I/20
1,8
1,84
1,88
1,91
1,94
1,96
1,97
1,98
1,99
1,99
1,99
ln(I) - I/10
1,3
19
18
16
14
11
1,17
1,13
1,09
1,04
0,99
Decision making under conditions of uncertainty
F 1
F 2
...
Fn
E 1
e 11
e 12
...
e 1n
E 2
e 21
e 22
...
e 2n
...
...
...
...
...
E m
e m1
e m2
...
e mn
Classic decision criteria
1. Minimax criterion.
2. Bayes-Laplace criterion.
3. Savage criterion.
4. Example and conclusions.
F 1
F 2
F 3
MM criterion
criterion B-L
e ir = min j (e ij)
max i (e ir)
e ir = ∑e ij
max i (e ir)
E 1
-20,0
-20
-25,0
-25,0
-25,0
-22,33
E 2
-14,0
-23,0
-31,0
-31,0
-22,67
E 3
0
-24.0
-40.0
-40.0
-21.33
-21.33
F 1
F 2
F 3
Savage criterion
e ir = min j (a ij)
min j (e ir)
E 1
+20,0
0
0
+20,0
E 2
+14,0
+1,0
+6,0
+14,0
+14,0
E 3
0
+2,0
+15,0
+15,0
Derived criteria.
1. Hurwitz criterion.
2. Hodge–Lehman criterion.
3. Germeier criterion.
4. Combined Bayes-Laplace and minimax criterion.
5. Criterion of works.
Example.
||e ij ||
С⋅min j (e ij)
(1-С)⋅max j (e ij)
e ir
max i (e ir)
-20,0
-22,0
-25,0
-12,5
-10.0
-22,5
-14,0
-23.0
-31.0
-15,5
-7.0
-22,5
0
-24.0
-40.0
-20.0
0
-20.0
-20.0
∑e ij ⋅q j
min j (e ij)
v⋅∑e ij ⋅q j
(1-v)⋅∑e ij ⋅q j
e ir
max i (e ir)
-22,33
-25,0
-11,17
-12,5
-23,67
-23,67
-22,67
-31,0
-11,34
-15,5
-26,84
-21,33
-40,0
-10,67
-20,0
-30,76
||e ij ||
||e ij q j ||
e ir = min j (e ij q j)
max i (e ir)
-20,0
-22,0
-25,0
-6,67
-7,33
-8,33
-8,33
-8,33
-14,0
-23,0
-31,.0
-4,67
-7,67
-10,33
-10,33
0
-24,0
-40,0
0
-8,0
-13,33
-13,33
||e ij ||
∑e ij q j
e i 0 j 0 - min j (e ij)
max j (e ij)
max j (e ij) - max j (e i 0 j)
-20,0
-22,0
-25,0
-23,33
0
-20,0
0
-14,0
-23,0
-31,0
-22,67
+6,0
-14,0
+6,0
0
-24,0
-40,0
-21,33
+15,0
0
+20,0
a
||e ij + a||
e ir = ∏ j e ij
max i e ir
41
+21
+19
+16
6384
6384
+27
+18
+10
4860
+41
+17
+1
697
200
+180
+178
+175
5607
+186
+177
+169
5563
+200
+176
+160
5632
5632